B. Наличие сезонного спроса

A. Относительно равномерный спрос

 

Относительно равномерный (или базовый) спрос характерен для регулярно потребляемых запасов, не имеющих сезонных периодов потребления. Относительно равномерный спрос типичен для запасов основных материалов производственных предприятий. Для прогнозирования потребности в запасах, характеризуемых временными рядами отгрузок равномерного характера, можно использовать методы наивного прогноза и группу методов прогнозирования по среднему значению (простой средней, скользящей средней,взвешенной скользящей средней), а так же метод экспоненциального сглаживания (см. Рисунок 43).

На примере потребления запаса за два года (см. Таблица 17) проиллюстрируем простейшие методы прогнозирования, а именно

1) наивный прогноз,

2) прогнозирование по средним значениям,

3) метод экспоненциального сглаживания.

Таблица 17

Временной ряд отгрузок товара со склада

Месяц	Фактические отгрузки
Предыдущий год
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь
Текущий год
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

 

 

(1) Наивный прогноз является самой простой методикой прогнозирования. Она основывается на предположении о том, что прогнозируемое потребление будущего периода равно потреблению предшествующего периода.

Пример наивного прогноза потребности в запасах по текущему году представлен в Таблица 17 и на Рисунок 44. Результаты прогнозирования демонстрируют отставание прогнозных значений от фактически реализуемых.

Таблица 18

Пример наивного прогнозирования потребления запаса в предыдущем году

 

Месяц	Фактические отгрузки	Наивный прогноз
январь		-
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

 

 

Рисунок 44. Результаты наивного прогнозирования потребности в запасах.

 

Может показаться, что наивное прогнозирование является чрезмерно упрощенным методом. В то же время необходимо отметить и сильные стороны такого приема. Для проведения наивного прогноза не требуется наличия накопленной статистической базы. Наивный прогноз позволяет работать и при ее отсутствии. Наивный прогноз понятен, прост в подготовке, быстр в реализации, не требует, фактически, никаких затрат. Основным недостатком наивного прогнозирования является вероятная низкая точность прогноза, как, например, в случае Рисунок 44.

Другие методы прогнозирования, которые будут рассмотрены в данном разделе, могут привести к более точным результатам, чем метод наивного прогнозирования, но, являясь более сложными, могут потребовать и более высоких затрат на их применение. Поэтому по критерию соотношения затрат на реализацию и точности прогнозирования менеджеры должны определиться, какой метод прогнозирования следует применять. Вполне возможно, что таким методом окажется метод наивного прогноза.

(2) Прогнозирование по средним значениям.В случае если временной ряд имеет интервал наблюдений в один месяц, повысить точность наивного прогноза позволяет (а)метод прогнозирования по простой средней величине потребления с учетом количества рабочих дней в месяце.

Для рассматриваемого примера (см. Таблица 17) количество рабочих дней по месяцам предыдущего года представлено в Таблица 19 столбец 3.

 

Таблица 19

Прогноз потребления предыдущего года на основе среднедневного потребления

 

Месяц	Фактические отгрузки за месяц	Количество рабочих дней	Среднее потребление в день	Прогноз среднедневного потребления	Прогноз месячного потребления
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

 

 

Динамика фактических отгрузок по месяцам (см. столбец 2 Таблица 19) приведена на Рисунок 45. Динамика среднедневного потребления запаса по месяцам (см. столбец 4Таблица 19) представлена на Рисунок 46.

 

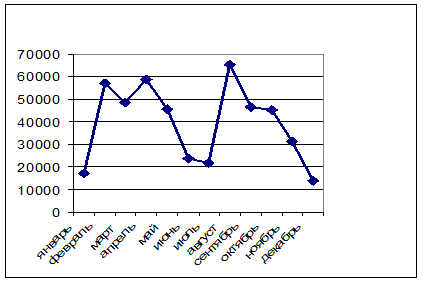
Рисунок 45. Динамика фактических отгрузок товара по месяцам.

 

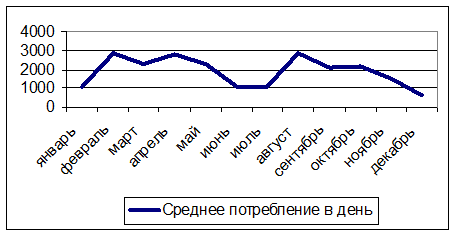
Рисунок 46. Динамика среднедневного потребления запасов по месяцам.

 

Сравнение Рисунок 45 и Рисунок 46 показывает, что учет количества рабочих дней позволяет более верно отразить фактические отгрузки. Так, например, рост потребности в январе-феврале по месячным оценкам составил приблизительно 2,3 раза ( ), а по среднедневным оценкам – приблизительно 1,7 раза ( ). Учет меньшего количества рабочих дней в январе по сравнению с февралем позволяет более точно определить реальное положение вещей.

Для расчета среднедневного потребления, например, в январе месяце требуется разделить фактические отгрузки в январе месяце на количество рабочих дней месяца:

 

17244 / 16 = 1077,75 ≈ 1078.

Формула 31

 

При получении дробной величины среднедневного потребления округление производится в большую сторону, чтобы исключить нехватку запаса при обеспечении потребности.

В феврале месяце среднедневная потребность составит

 

57187 / 20 = 2859,35 ≈ 2860.

Формула 32

 

Прогноз среднедневного потребления делается на основе расчета среднедневного потребления в предыдущем месяце. Для февраля месяца прогноз среднедневного потребления составит 1078 единиц (см. Таблица 19 и Формула 31), для марта месяца – 2860 единиц (см. Формула 32) и т.д.

Прогноз месячного потребления (см. столбец 6 Таблица 19) рассчитывается как произведение прогноза среднедневного потребления на количество рабочих дней в соответствующем месяце. Например, для февраля месяца прогноз среднемесячного потребления составит

 

1078 * 20 = 21560.

 

Иллюстрация результатов прогнозирования по средней величине потребления с учетом количества рабочих дней месяцев в сравнении с результатами наивного прогноза приведена на Рисунок 47. Как видно из рисунка, прогноз потребления с учетом количества рабочих дней по месяцам приводит в абсолютном большинстве случаев к более точному результату, что наивный прогноз.

 

Рисунок 47. Результаты прогнозирования потребности в запасах на основе среднедневного потребления.

 

Еще одним методом прогнозирования, относящимся к прогнозированию по средним значениям, является (б) прогноз на основе скользящего среднего значенияпотребления запаса.

Метод скользящей средней при составлении прогноза использует значение средней арифметической величины потребления за последние периоды наблюдений. Скользящая средняя рассчитывается по следующей формуле:

,

Формула 33

где – прогнозируемый объем потребности в j-ом периоде времени, единиц;

i – индекс предыдущего периода времени;

Р_i – объем потребления в i-ом предыдущем периоде времени;

n – количество периодов, используемых в расчете скользящей средней.

 

Для составления прогноза по скользящей средней требуется определиться в количестве периодов наблюдений n, которые будут использоваться в расчете. При этом требуется учитывать особенности имеющегося временного ряда. Чем большее количество точек наблюдения берется в расчет, тем скользящая средняя менее чувствительная к изменениям значений потребления в прошлые периоды. Если изменение наблюдений имеет ступенчатый характер, то следует обеспечить высокую чувствительность прогноза к каждому из наблюдений. Это требует использования возможно меньшего количества наблюдений.

В примере, который разбирается в данном разделе (см. Таблица 19 и Рисунок 47) колебания спроса в течение первой половины года не длятся более 2 месяцев. Во второй половине года имеются более длительные тенденции (до 4 месяцев в конце года). Игнорируя пока характер сезонных колебаний и тенденции рассматриваемого примера, выберем в качества интервала расчета скользящей средней 2 месяца. Результат расчет прогноза по скользящей средней с учетом количества рабочих дней в месяцах приведен в Таблица 20.

 

Таблица 20

Расчет прогнозного значения потребления запаса по скользящей средней

Месяц	Фактические отгрузки за месяц	Количество рабочих дней	Среднее потребление в день	Прогноз среднедневной потребности	Прогноз месячной потребности
январь				-	-
февраль				-	-
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

 

Для получения прогноза среднедневной потребности (см. столбец 5 Таблица 20), например, в марте месяце требуется использовать статистику фактических среднедневных отгрузок в январе и феврале месяце (см. столбец 4 Таблица 20):

 

(1078 + 2859) / 2 = 1968,5 ≈ 1969.

Формула 34

 

Для прогнозирования среднедневной потребности в апреле (см. столбец 5 Таблица 20) требуется использовать статистику фактических среднедневных отгрузок в феврале и марте месяце (см. столбец 4 Таблица 20):

 

(2859 + 2310) / 2 = 2584,5 ≈ 2585.

 

Округление полученной средней величины потребления ведется до целого числа в большую сторону для обеспечения гарантии покрытия потребности запасом.

Для получения прогноза месячной потребности (см. столбец 6 Таблица 20), например, в марте месяце требуется прогноз среднедневного потребления в марте месяце (см. столбец 5 Таблица 20)умножить на количество рабочих дней в этом месяце (см. столбец 3 Таблица 20 и Формула 34):

 

1969 * 21 = 41349.

 

Иллюстрация результатов прогнозирования по скользящей средней с учетом количества рабочих дней в месяцах приведена на Рисунок 48.

 

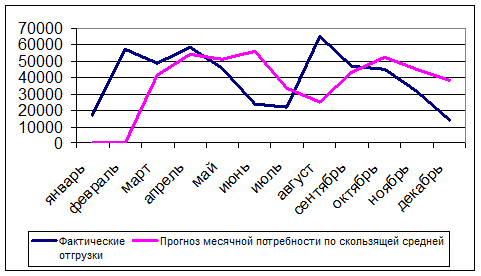
Рисунок 48. Результаты прогнозирования потребности в запасах методом скользящей средней.

 

Преимущество прогнозирования по скользящей средней состоит в простоте метода. Основным недостатком является то, что значимость значений прошлых периодов при прогнозировании будущей потребности одинакова. Например, если в расчете скользящей средней используется 6 значений, то значимость каждого значения равна 1/6. Между тем, очевидно, что значимость статистики последнего из предшествующих периодов более велика, чем предыдущих.

Для учета важности отдельных периодов наблюдений используют (в) метод взвешенной скользящей средней. В этом методе каждому используемому в расчете скользящей средней периоду присваивается коэффициент, отражающий значимость влияния этого периода на прогнозное значение потребления. Значимость более поздних периодов должна быть выше, чем значимость более ранних периодов. Например, из 6-ти периодов расчета скользящей средней последнему может быть присвоен удельный вес 5, предыдущему - 4, далее 3; 2; 1 и 1. В общем виде взвешенная скользящая средняя рассчитывается следующим образом:

 

,

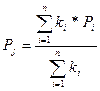Формула 35

где Р_j – прогнозируемый объем потребности в j-ом периоде времени, единиц;

i – индекс предыдущего периода времени;

k_i - коэффициент значимости i-го периода времени;

Р_i – объем потребления в i-ом предыдущем периоде времени, единиц;

n – количество используемых в расчете предыдущих периодов времени.

 

Для рассматриваемого в этом разделе примера (см. Таблица 20 и комментарий к ней) выберем коэффициенты значимости прошлых периодов при прогнозировании потребности будущего периода. Для последнего периода коэффициент значимости принимается равным 5, для предпоследнего - 1. Расчет взвешенной скользящей средней приведен вТаблица 21.

 

Таблица 21

Расчет прогноза потребления запаса по взвешенной скользящей средней

 

Месяц	Фактические отгрузки за месяц	Количество рабочих дней	Среднее потребление в день	Прогноз среднедневной потребности	Прогноз месячной потребности
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

 

Для расчета прогноза среднедневного потребления запаса (см. столбец 5 Таблица 21), например, в марте месяце требуется статистика фактических среднедневных отгрузок (см. столбец 2 Таблица 21) за январь и февраль месяцы:

 

(2859*5+1078*1) / 6 = 2562, 17 ≈ 2563.

 

Округление произведено в большую сторону для гарантии обеспечения потребности запасом.

Для получения прогноза месячной потребности в марте месяце (см. столбец 6 Таблица 21) надо прогноз среднесуточной потребности в марте (см. столбец 5 Таблица 21) умножить на количество рабочих дней в этом месяце (см. столбец 3 Таблица 21):

 

2563*21 = 53823.

 

Иллюстрация результатов прогнозирования потребности в запасах на основе взвешенной скользящей средней (см. Таблица 21) приведена на Рисунок 49.

 

Рисунок 49. Результаты прогнозирования потребности в запасах методом взвешенной скользящей средней.

 

В целом, прогнозирование по взвешенной скользящей средней дает более точные результаты, чем по простой скользящей средней. Главное преимущество взвешивания состоит в том, что в прогнозируемой величине в большей степени учитываются последние значения потребности. Определенную проблему представляет собой подбор коэффициентов значимости. Они, как правило, определяются экспертно и проверяются экспериментально, то есть путем проб и ошибок.

Более сложный метод прогнозирования на основе расчета взвешенного среднего – это (3) метод экспоненциального сглаживания (см. Рисунок 43). В этом методе каждый новый прогноз основан на учете значения предыдущего прогноза и его отклонения от фактического значения. Прогнозное значение по методу экспоненциального сглаживания определяется следующим образом:

 

Прогнозное значение =

Значение предыдущего прогноза

+

а*(Фактическая потребность – Значение предыдущего прогноза)

 

или

 

Р_j = P_j-1 + a*(F_j-1 – P_j-1),

Формула 36

где Р_j – прогнозируемый объем потребности в j-ом периоде времени, единиц;

Р_j-1 – прогнозируемый объем потребности в (j-1)-ом периоде времени, единиц;

а – константа сглаживания,

F_j-1 – фактическая потребность в (j-1)-ом периоде, единиц.

 

Константа сглаживания а определяет чувствительность прогноза к ошибке. Чем ближе ее значение к нулю, тем медленнее прогноз будет реагировать на ошибки. Тем, следовательно, будет выше степень сглаживания прогноза. Напротив, чем ближе значение сглаживающей константы к единице, тем выше чувствительность и меньше сглаживание. Подбор значения константы сглаживания проводится экспериментально. Цель такого подбора состоит в том, чтобы определить такое значение а, чтобы, с одной стороны, прогноз был чувствителен к изменениям временного ряда, а с другой стороны, хорошо сглаживал скачки потребления, вызванные случайными факторами.

Пример расчета прогноза при константе сглаживания равной 0,2 и 0,8 приведен в Таблица 22.

 

Таблица 22

Расчет прогноза потребления запаса по методу экспоненциального сглаживания

Месяц	Фактические отгрузки	Количество рабочих дней	Среднее потребление в день	Прогноз среднедневной потребности при а=0,2	Прогноз месячной потребности методом при а=0,2	Прогноз дневной потребности при а=0,8	Прогноз месячной потребности при а=0,8
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

 

Для расчета прогнозного значения потребления запаса в апреле месяце использована величина прогнозной оценки отгрузки в марте месяце по взвешенной скользящей средней (см. Таблица 21 и столбцы 5 и 7 Таблица 22). Величина прогнозного значения дневной потребности в запасах в апреле месяце рассчитывается при значениях константы сглаживания а=0,2 или а=0,8 следующим образом:

 

2563+0,2*(2310-2563) = 2512,4 ≈ 2513

Формула 37

и

 

2563+0,8*(2310-2563) = 2360,6 ≈ 2361.

Формула 38

Для мая месяца расчет проводится следующим образом:

 

2513+0,2*(2793-2513) = 2569

Формула 39

и

 

2513+0,8*(2793-2513) = 2737 и т.д.

Формула 40

Округления полученных значений проводятся до ближайшего большего целого числа.

Для получения прогноза месячной потребности (см. столбцы 6 и 8 Таблица 22) следует умножить прогноз среднедневного потребления (см. столбцы 5 и 7 Таблица 22) на количество рабочих дней соответствующего месяца (см. столбец 3 Таблица 22):

для апреля месяца (см. Формула 37 и Формула 38):

 

2513*21 = 52773 и 2361*21 = 49581;

 

для мая месяца (см. Формула 39 и Формула 40):

 

2569*20 = 51380 и 2737*20 = 54740.

Для выявления, при каком значении константы сглаживания (а = 0,2 или а = 0,8) прогноз Таблица 22 (см. так же Рисунок 50) имеет более высокую точность следует провести оценку точности прогноза. Методы оценки точности прогноза приведены в п. 6.4.1.

 

Рисунок 50. Результаты прогнозирования потребности в запасах методом экспоненциального сглаживания.

 

В практике довольно часты случаи, когда запасы отгружаются неравномерно. В неравномерности могут присутствовать сразу несколько составляющих. Разберем их последовательно.

 

 

b. Наличие сезонного спроса

 

Спрос является сезонным, если в нем имеются краткосрочные (менее года) регулярные изменения, связанные с погодой или с определенными календарными периодами (время отпусков, праздники, времена года и пр.). Сезонный спрос проявляется в периодическом увеличении или уменьшении спроса в течение года.

В рассматриваемом в этом разделе примере (см. Таблица 17) характерна явно выраженная сезонная тенденция спроса: пик отгрузок приходятся на март-апрель и сентябрь-октябрь двух следующих друг за другом года (см. Рисунок 51). Соответственно, в январе-феврале и в июле-августе наблюдаются относительное повышение спроса, а в мае-июне и в ноябре-декабре – спады.

 

Рисунок 51. Динамика отгрузок запаса товара за два года.

 

Для прогнозирования такого явно выраженного сезонного спроса требуется использовать статистику отгрузок соответствующих периодов прошлых лет. Проиллюстрируем возможности прогнозирования сезонного спроса в периоде роста и спада спроса на примере Таблица 17.

Таблица 17 содержит временные ряды фактических отгрузок за три года: текущий год, предыдущий год и год, предшествующий предыдущему. Текущий год имеет как данные по фактической отгрузке запасов, так и данные прогнозных оценок отгрузки. Прогноз потребления запасов в текущем году выполнен на основе вывода о наличии сезонного спроса на товар (см. Рисунок 51). Расчет проводился по методу взвешенной скользящей средней по данным двух предшествующих годов. Результаты расчетов приведены в Таблица 23.

Таблица 23

Результаты прогнозирования сезонной потребности в запасах по взвешенной скользящей средней.

Год, предшествующий предыдущему

Предыдущий год

Текущий год

Месяц

Фактические отгрузки

Количество рабочих дней

Среднедневное потребление

Месяц

Фактические отгрузки

Количество рабочих дней

Среднедневное потребление

Месяц

Фактические отгрузки

Количество рабочих дней

Среднедневное потребление

Прогноз среднедневной потребности

Прогноз месячной потребности

январь

январь

январь

февраль

февраль

февраль

март

март

март

апрель

апрель

апрель

май

май

май

июнь

июнь

июнь

июль

июль

июль

август

август

август

сентябрь

сентябрь

сентябрь

октябрь

октябрь

октябрь

ноябрь

ноябрь

ноябрь

декабрь

декабрь

декабрь

 

Для получения прогноза среднедневной потребности (см. столбец 13 Таблица 23), например, в январе месяца текущего года были использованы коэффициенты значимости предыдущего года в размере 5 и года, предшествующего предыдущему, – 1. Прогноз среднедневной потребности был рассчитан следующим образом:

 

(объем фактических среднедневных отгрузок января года, предшествующего предыдущему,

*

коэффициент значимости данного года

+

объем фактических среднедневных отгрузок января предыдущего года

*

коэффициент значимости данного года)

/

сумма коэффициентов значимости предшествующего предыдущему и предыдущего годов

Формула 41

 

или

 

(1265 * 5 + 1878 * 1) / 6 = 1367, 17 ≈ 1368,

 

где коэффициент значимости года, предшествующего предыдущему, равен 1, а коэффициент значимости предыдущего года равен 5.

 

Прогноз месячной потребности (см. столбец 14 Таблица 23) определяется как произведение прогноза среднедневной потребности (столбец 13Таблица 23) на количество рабочих дней в соответствующем месяце прогнозируемого года (столбец 11 Таблица 23):

 

1368 * 16 = 21888.

 

На Рисунок 52 приведена иллюстрация результатов прогнозирования сезонной потребности (см. столбец 14 Таблица 23). Прогнозирование выявленной сезонной потребности дает лучший результат по сравнению с прогнозированием методом наивного прогноза (см. Рисунок 44), простой средней (см. Рисунок 47), скользящей средней (см. Рисунок 48) взвешенной скользящей средней (см. Рисунок 49) и методом экспоненциального сглаживания (см. Рисунок 50).

 

Рисунок 52. Результаты прогнозирования сезонной потребности в запасах методом взвешенной скользящей средней.