Способы задания функции

Задать функцию – это значит указать правило, позволяющее по данному значению независимой переменной находить соответствующее значение функции.

Существует три основных способа задания функции: аналитический, табличный и графический.

Аналитический способ состоит в том, что зависимость между переменными величинами задается в виде формулы (аналитического выражения), указывающей, какие и в каком порядке действия надо выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.

Например, ; ; , где .

Аналитический способ является наиболее совершенным, т.к. к нему могут быть применены методы математического анализа, позволяющие полностью исследовать функцию.

Табличный способ предусматривает задание таблицы, в которой различным значениям аргумента поставлены соответствующие значения функции :

 

х	х1	х2	…	хn
y	y1	y2	…	yn

Такие таблицы составляются, например, по данным эксперимента; для облегчения вычислений с часто встречающимися функциями (таблицы логарифмов, таблицы тригонометрических функций и т.д.).

Графический способ задания функции состоит в том, что в данной системе координат задается некоторая кривая. Преимуществом графического задания является его наглядность, недостатком – его неточность.

 

 

Основные элементарные функции

Основными элементарным функциями называются следующие функции:

1) Степенная функция

, .

2) Показательная функция

.

3) Логарифмическая функция

.

4) Тригонометрические функции

.

5) Обратные тригонометрические функции

.

 

 

Сложная функция

Из основных элементарных функций можно строить другие функции при помощи новой операции взятия функции от функции.

Пусть y является функцией от u, т.е. , а u, в свою очередь, зависит от переменной х, т.е. . Тогда y также зависит от х:

.

Функция называется сложной функцией, или функцией от функции, или суперпозицией функций.

Переменную называют промежуточным аргументом сложной функции, а х – независимой переменной.

Операция взятия функции от функции может проводиться любое число раз. Например, функция есть суперпозиция трех функций , и .

Сложная функция может иметь несколько промежуточных аргументов.

 

Обратная функция

Определение.

Пусть функция , определена на множестве Х с областью значений Y. Если каждому соответствует единственное , при котором , то функция называется обратной (рис.1.3).

 

 

 

Рис. 1.3

 

Поскольку традиционно независимую переменную принято обозначать через х, а зависимую (функцию) – через y, то обратная функция для х примет вид: . Это соответствие часто записывают также в виде . следует воспринимать как символ для обозначения обратной функции, а не как . Например, для функции обратной функцией будет . В полученном выражении поменяем местами х и y, тогда 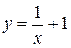– обратная функция.

 

 

Элементарные функции

Определение.

Функции, полученные из основных элементарных функций и постоянных при помощи конечного числа арифметических действий и конечного числа операций взятия функции от функции, называются элементарными функциями.

Например, ; ; ; .

Элементарные функции делятся на алгебраические и трансцендентные.

К алгебраическим относятся следующие функции:

1) Целая рациональная функция или многочлен:

,

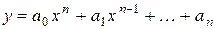где – числа, называемые коэффициентами, степень многочлена.

Например, .

2) Дробная рациональная функция.

Эта функция является отношением двух многочленов:

.

Например, .

3) Иррациональная функция.

Например, ; .

Функция, не являющаяся алгебраической, называется трансцендентной.

Например, ; ; .