 |
Главная |
Алгоритм исчисления порядка
|
из
5.00
|
Вход: g – порождающий элемент циклической группы порядка n, a 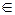 G, с≈10 – параметр надежности.
G, с≈10 – параметр надежности.
Ш.1. Выбирается факторная база S={p1, p2,…,pt}. (Если G=Zp*, то S состоит из t первых простых чисел.)
Ш.2. Выбрать случайное k: 0≤k<n и вычислить gk.
Ш.3. Попытаться разложить gk по факторной базе:
 , αi≥0.
, αi≥0.
Если это не удалось, вернуться на Шаг 2.
Ш.4. Логарифмируя обе части получившегося выражения, получаем
 (mod n) *
(mod n) *
В этом выражении неизвестными являются логарифмы.
Это сравнение с t неизвестными следует запомнить.
Ш.5. Если сравнений вида (*), полученных на Шаге 4, меньше, чем t+c, то вернуться на Шаг 2.
Ш.6. Решить систему t+c сравнений с t неизвестными вида (*), составленную на Шагах 2-5.
Ш.7. Выбрать случайное k: 0≤k<n и вычислить agk.
Ш.8. Попытаться разложить agk по факторной базе:
 , βi≥0.
, βi≥0.
Если это не удалось, вернуться на Шаг 7.
Ш.9. Логарифмируя обе части последнего равенства, получаем
x=  ,
,
где loggpi (1≤i≤t) вычислены на Шаге 6 как решение системы сравнений.
Выход. x = logga mod n.
В том случае, когда G=Zp*, в качестве факторной базы S берут t первых простых чисел. Такой выбор оправдан следующим наблюдением. Число, наугад выбранное из множества целых чисел, с вероятностью 1/2 делится на 2, с вероятностью 1/3 – на 3, с вероятностью 1/5 – на 5 и т.д. Поэтому можно ожидать, что в промежутке от 1 до p—1 найдется достаточно много чисел, в разложении которых участвуют только маленькие простые делители из множества S. Именно такие числа отыскиваются на шагах 2 и 7.
Параметр c вводится для того, чтобы система сравнений, решаемая на Шаге 6, имела единственное решение. Дело в том, что полученная система может содержать линейно зависимые сравнения. Считается, что при значении с порядка 10 и большом p система сравнений имеет единственное решение с высокой вероятностью.
Пример.
G=Z*71, g=7, a=17, n=φ(71)=70.
S={2, 3, 5, 7} (Шаг 1). (Можем сразу указать log77 mod 70=1).
Теперь будем перебирать k для составления системы сравнений вида * (Шаги 2—5).
k=2, 72 mod 71=49=7·7. (поскольку log77 уже вычислен, это сравнение нам не пригодится).
k=3, 73 mod 71=59.
k=4, 74 mod 71=58=2·29.
k=5, 75 mod 71=51=3·17.
k=6, 76 mod 71=2 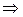 6≡log72(mod 70)
6≡log72(mod 70)
k=7, 77 mod 71=14=2·7 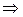 7≡log72+log77(mod 70)
7≡log72+log77(mod 70)
k=8, 78 mod 71=27=33 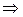 8≡3log73(mod 70)
8≡3log73(mod 70)
k=9, 79 mod 71=47.
k=10, 710 mod 71=45=32·5  10≡2log73+log75(mod 70)
10≡2log73+log75(mod 70)
Теперь имеем достаточно сравнений для того, чтобы определить логарифмы от элементов факторной базы. Вот эти сравнения:
6≡log72(mod 70)
7≡log72+log77(mod 70)
8≡3log73(mod 70)
10≡2log73+log75(mod 70)
Решая полученную систему, получаем (Шаг 6):
log72≡6(mod 70), log73≡26(mod 70),
log75≡28(mod 70), log77≡1(mod 70).
Перейдем к Шагам 7—9:
k=1, 26·7 mod 71=40=23·5  log726≡3log72+log75—1(mod 70)
log726≡3log72+log75—1(mod 70) 
log726≡3·6+28—1(mod 70)
log726≡45(mod 70)
Проверка: 745 mod 71 = 26. Верно.
Ответ: log726≡45(mod 70).
Замечание: Для случая G=Zp и для случая G=F2m составляет Lq[1/2,c], где q есть мощность G, с > 0 – константа. Алгоритм, имеющий наилучшую оценку сложности (по времени) для дискретного логарифмирования в Zp есть вариант алгоритма исчисления индексов под названием «метод решета числового поля» (number field sieve), для дискретного логарифмирования в F2m - вариант данного алгоритма под названием «алгоритм Копперсмита» (Coppersmith’s algorithm). Эти алгоритмы слишком сложны, чтобы приводить их здесь.
Задачи и упражнения.
Упражнения к Главе 1.
1.1. Вычислить НОД(a,b) при помощи алгоритма Евклида с делением с остатком и бинарного алгоритма Евклида. Сравнить количество итераций.
a) a = 715, b = 195; d) a = 1818, b = 726; g) a = 2448, b = 1632;
b) a = 246, b = 396; e) a= 6887, b = 6319; h) a = 1600, b = 1120;
c) a = 175, b = 14945; f) a = 1763, b = 1634; i) a = 2310, b = 3388.
1.2. Пользуясь таблицей простых чисел, найти канонические разложения следующих чисел:
a) 492; d) 4144; g) 624239;
b) 22011; e) 2597; h) 422375;
c) 7533; f) 425106; i) 11502.
1.3. Вычислить НОК(a,b).
a) a = 744, b = 198; d) a = 50, b = 42; g) a = 3131, b = 808;
b) a = 60, b = 1575; e) a= 231, b = 1089; h) a = 1063, b = 3;
c) a = 128, b = 81; f) a = 73, b = 219; i) a = 1960, b = 1232.
1.4. Пользуясь свойствами функции Эйлера, вычислить φ(a).
a) a = 73; d) a = 343; g) a = 210;
b) a = 81; e) a= 6; h) a = 10800;
c) a = 97; f) a = 28; i) a = 32.
1.5. Выяснить, верны ли сравнения:
a) 25 ≡ —1 (mod 13); d) 3 ≡ 15 (mod 11); g) 128 ≡ 20 (mod 9);
b) 11 ≡ 3 (mod 2); e) 45 ≡ 12 (mod 11); h) 32 ≡ 5 (mod 7);
c) 100 ≡ 14 (mod 17); f) 98 ≡ 46 (mod 5); i) 13 ≡ 1 (mod 14).
1.6. Выписать полную и приведенную системы вычетов по модулю n. Сравнить количество чисел в приведенной системе вычетов со значением функции Эйлера от n.
a) n = 7; b) n = 9; c) n = 11; d) n = 16; e) n = 6; f) n = 2;
1.7. Вычислить абсолютно наименьший и наименьший неотрицательный вычеты числа a по модулю m.
a) a = 12, m = 15; d) a = 50, m = 12; g) a = —80 , m = 100;
b) a = 35, m = 31; e) a= 8, m = 15; h) a = —4, m = 3;
c) a = —1, m = 81; f) a = 8, m = 17; i) a = 11, m = 11.
1.8. Вычислить обратный элемент, если он существует:
a) 5-1 mod 8; d) 14-1 mod 25; g) 46-1 mod 51;
b) 7-1 mod 41; e) 13-1 mod 92; h) 77-1 mod 101;
c) 23-1 mod 63; f) 9-1 mod 27; i) 22-1 mod 25.
1.9. Пользуясь теоремой Эйлера, вычислить:
a) 9042 mod 41; d) 8485 mod 187; g) 3161613 mod 16;
b) 34160003 mod 15; e) (-2)634178 mod 117; h) 5186609 mod 9;
c) (-5)100016 mod 11; f) 50190021 mod 38; i) 347174007 mod 349;
1.10. Решить сравнения:
a) 5x ≡ 3(mod 11); d) 6x ≡15(mod 21); g) 13x≡8(mod 16);
b) 8x ≡ 5(mod 13); e) 16x≡26(mod 62); h) 25x≡50(mod 125);
c) 15x≡25(mod 17); f) 21x≡14(mod 42); i) 13x≡37(mod 29).
1.11. Решить системы сравнений.
a)  ; c)
; c)  ; e)
; e)  ;
;
b) 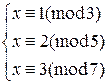 ; d)
; d)  ; f)
; f)  .
.
1.12. Вычислить, пользуясь свойствами символа Якоби:
a)  ; c)
; c) 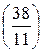 ; e)
; e) 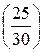 ; g)
; g)  ; i)
; i)  ; k)
; k)  ;
;
b) 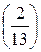 ; d)
; d)  ; f)
; f) 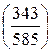 ; h)
; h)  ; j)
; j)  ; l)
; l)  .
.
1.13. Решить следующие квадратичные сравнения по простому модулю, если решение существует.
a) x2≡17(mod 19); d) x2≡2 (mod 7); g) x2≡3 (mod 41);
b) x2≡3 (mod 13); e) x2≡3 (mod 11); h) x2≡2 (mod 17);
c) x2≡8 (mod 41); f) 2x2≡10 (mod 11); i) 3x2≡15(mod 31).
1.14. Решить следующие квадратичные сравнения по составному модулю, если решение существует.
a) x2≡7(mod 9); g) x2≡1 (mod 32); m) x2≡11 (mod 35);
b) x2≡—1(mod 25); h) x2≡67 (mod 81); n) x2≡5 (mod 12);
c) x2≡32(mod 49); i) x2≡59 (mod 125); o) x2≡9 (mod 20);
d) x2≡1(mod 4); j) x2≡4(mod 6); p) x2≡31 (mod 105);
e) x2≡3(mod 8); k) x2≡1(mod 15); q) x2≡4 (mod 105);
f) x2≡9(mod 16); l) x2≡1(mod 24); r) x2≡ 16 (mod 75).
1.15. Определить, сколько решений имеют сравнения.
a) x2≡—1(mod 59); d) x2≡ 17(mod 32); g) x2≡1(mod 150);
b) x2≡ 3(mod 83); e) x2≡ 25(mod 96); h) x2≡4(mod 343);
c) x2≡ 1(mod 8); f) x2≡ 2(mod 315); i) x2≡1(mod 2).
1.16. Выписать все квадраты и все псевдоквадраты из приведенной системы вычетов по модулю n.
a) n = 15; b) n = 21; c) n = 33; d) n = 6; e) n = 14; f) n = 35.
1.17. Указать, какие их приведенных ниже чисел являются числами Блюма.
a) 7; b) 21; c) 47; d) 469; e) 35; f) 59.
1.18. Отыскать p8 и p9 – 8-е и 9-е простые числа, представимые в виде 4k+3. Составить число Блюма n=p8p9. На основе BBS-генератора с ключом s0=121 составить ключевую последовательность длиной 10 бит.
1.19. Существуют ли первообразные корни по модулю n, и если существуют, то сколько их?
a) n = 15; b) n = 71; c) n = 53; d) n = 202; e) n = 16; f) n = 25.
1.20. Найти первообразные корни по следующим модулям:
a) 3; c) 27; e) 26; g) 43; i) 169; k) 89;
b) 9; d) 13; f) 18; h) 86; j) 4; l) 41.
Упражнения к Главе 2.
2.1. Вычислить сумму и произведение многочленов f(x) и g(x) на Z2[x]:
a) f(x)=x7+x5+x+1, g(x)=x4+x+1; c) f(x)=x8+x2, g(x)=x3+x2+1;
b) f(x)=x4+x, g(x)=x2+1; d) f(x)=x5; g(x)=x5+x.
2.2. Вычислить остаток от деления f(x) на g(x) на Z2[x].
a) f(x)=x8+x4+x+1, g(x)=x3+x+1; c) f(x)=x10+x2+x+1, g(x)=x2+x+1;
b) f(x)=x4+x, g(x)=x2+x+1; d) f(x)=x5+x4+1; g(x)=x2+x.
2.3. Вычислить НОД(g(x),f(x)) на Z2[x].
a) f(x)=x6+x5+x3+x2+1, g(x)= x5+x4+x+1;
b) f(x)=x6+x4, g(x)=x4+1;
c) f(x)=x4+x3+x2+x, g(x)=x5+x3;
d) f(x)=x9+x8+x; g(x)=x7+x4+x3+1.
Упражнения к Главе 3:
3.1. Осуществить 2-факторизацию следующих чисел, используя метод Ферма и метод квадратичного решета с решетами по модулям 4, 5, 7. Сравнить количество итераций для этих двух методов.
a) 12317; c) 7081; e) 551; g) 1679; i) 6111; k) 1221;
b) 851; d) 18161; f) 481; h) 7313; j) 1197; l) 609.
3.2. Осуществить 2-факторизацию следующих чисел, используя ро-метод Полларда.
a) 1183; b) 1881; c) 2597; d) 1057; e) 5461; f) 299.
3.3. Осуществить факторизацию следующих чисел, используя p—1 –метод Полларда.
a) 133; b) 209; c) 161; d) 527; e) 1393; f) 3277.
3.4. Вычислить следующие дискретные логарифмы, пользуясь алгоритмом «шаг младенца – шаг великана».
a) log3 14 mod φ(31); b) log5 42 mod φ(47); c) log3 30 mod φ(89).
3.5. При помощи алгоритма исчисления порядка вычислить следующие дискретные логарифмы.
a) log3 57 mod φ(89); b) log3 61 mod φ(79); c) log3 279 mod φ(587).
Ответы к упражнениям.
Упражнения к Главе 1:
1.1. a) 13, b) 2, c) 35, d) 6, e) 71, f) 43, g) 48, h) 160, i) 154.
1.2. a) 22·3·41, b) 3·11·23·29, c) 35·31, d) 24·7·37, e) 72·53, f) 2·32·11·19·131, g)7·113·67 h) 53·31·109, i) 2·34·71.
1.3. a) 24552, b) 6300, c) 10368, d) 1050, e) 7623, f) 219, g) 25048, h) 31189, i)43120.
1.4. a) 72, b) 54, c) 96, d) 294, e) 2, f) 12, g) 48, h) 2880, i) 16.
1.5. a) верно, b) верно, c) неверно, d) неверно, e) верно, f) неверно, g) верно, h)неверно, i) неверно.
1.7. a) —3; 12, b) 4; 4, c)—1; 80, d) 2; 2, e)—7; 8, f) 8; 8, g) 20; 20, h)—1; 2, i)0;0.
1.8. a) 5, b) 6, c) 11, d) 9, e) 7, f) не существует, g) 10, h) 21, i) 8.
1.9. a) 23, b) 4, c) 5, d) 43, e) 4, f) 18, g) 3, h) 8, i) 221.
1.10. a) x≡5(mod 11), b) x≡12(mod 13), c) x≡13(mod 17), d) x≡6, 15, 20(mod 21), e) x≡21, 52(mod 62); f) решений нет; g) x≡8(mod 16), h) x≡2+5t(mod 125), где t=  , i) x≡20(mod 29).
, i) x≡20(mod 29).
1.11. a) x≡8(mod 35), b) x≡52(mod 105), c) x≡53(mod 77), d) x≡101(mod 180), e) решений нет, f) x≡206(mod 210).
1.12. a) -1, b) -1, c) 1, d) 1, e) 0, f) 1, g) 1, h) 1, i) -1, j) -1, k) -1, l) -1.
1.13. a) ±6(mod 19), b) ±9(mod 13), c) ±7(mod 41), d) ±3(mod 7), e) ±5(mod 11), f) ±4(mod 11), g) решений нет, h) ±6(mod 17), i) ±6(mod 31).
1.14. a) ±4(mod 9), b) ±7(mod 25), c) ±9(mod 49), d) ±1(mod 4), e) решений нет, f) ±3, ±5(mod 16), g) ±1, ±15(mod 32), h) ±38(mod 81), i) ±53(mod 125), j) ±2(mod 6), k) ±1,±4(mod 15), l) ±1,±5,±7,±11(mod 24), m) ±9,±16(mod 35), n) решений нет, o) ±3,±7(mod 20), p) решений нет, q) ±2,±23,±37,±47(mod 105), r) ±4,±29 (mod 75).
1.15. a) решений нет, b) 2, c) 4, d) 4, e) 8, f) решений нет, g) 4, h) 2, i) 1.
1.18. 1011011101.
1.19. a) не существует, b) 24 корня, c) 24 корня, d) 40 корней, e) нет существует, f) 8 корней.
1.20. a) 3, b) 2, c) 2, d) 2, e) 17, f) 11, g) 3, h) 3, i) 2, j) 3, k) 3, l) 6.
Упражнения к Главе 2:
2.1. a) x7+x5+x4; x11+x9+x8+x7+x4+x2+1; b) x4+x2+x+1; x6+x4+x3+x; c) x8+x3+1; x11+x10+x8+x5+x4+x2; d) x; x10+x6.
2.2. a) x2+x+1, b) 0, c) x, d) 1.
2.3. a) (x+1), b) x2+1, c) x3+x, d) x2+x+1.
Упражнения к Главе 3:
3.4. a) 18, b) 24, c) 87.
3.5. a) 36, b) 45, c) 15.
Приложение 1.
Таблица простых чисел < 2558 и их наименьших первообразных корней.
| p | g | p | g | p | g | p | g | p | g | p | g | p | g | p | g |
| p | g | p | g | p | g | p | g | p | g | p | g | p | g |
Приложение 2.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
| . |
| ТЕОРЕТИКО - ЧИСЛОВЫЕ МЕТОДЫ В КРИПТОГРАФИИ |
| Рабочая программа для специальности |
| 075200 – Компьютерная безопасность |
Тюмень 2007
Пояснительная записка
|
из
5.00
|
Обсуждение в статье: Алгоритм исчисления порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

