 |
Главная |
Перечисляемый и диапазонный типы
|
из
5.00
|
Введение
Сборник содержит задания по языку программирования Паскаль [1, 3, 6, 8, 9, 10, 13] и ориентирован на версию, реализованную в наиболее распространенном компиляторе Turbo Pascal 7.0 [7, 11, 15, 18]. Набор упражнений составлен с учетом опыта проведения практических и лабораторных занятий по программированию на кафедре ЭВМ ЮУрГУ и в филиале ЮУрГУ в г. Нижневартовске. Использованы также упражнения из широко распространенных сборников [2, 5, 11, 14, 16, 17] и в первую очередь, конечно, из наиболее удачного и ставшего к настоящему времени библиографической редкостью задачника по Паскалю автора Пильщикова В.Н. [12].
Упражнения сборника охватывают основные темы программирования: вычислительные задачи, обработка одномерных и многомерных массивов, работа с текстами, записями, файлами, множествами, динамические типы данных. В каждом разделе представлены с необходимыми пояснениями листинги типовых задач, иллюстрирующие основные приемы программирования и алгоритмы, часто встречающиеся на практике.
Нумерация упражнений в каждом разделе начинается с 1. Многие упражнения имеют варианты, которые обозначаются начальными буквами русского алфавита. При ссылке на упражнения указывается номер раздела и номер упражнения в разделе, а если надо, то и буква варианта.
Для сокращения формулировок заданий в сборнике используются следующие соглашения. Все задания должны быть реализованы в виде законченных программ с описанием всех используемых констант, типов, переменных, процедур и функций, с вводом-выводом всех необходимых величин. Встречающиеся в упражнениях фразы типа «дано значение n» или «для заданных массивов A и B» указывают на то, что это значение или эти массивы являются исходными данными программы и должны быть в ней введены. Результатами же являются величины, которые надо «найти», «вычислить», «определить», «построить» и т.п. Идентификаторы в текстах заданий выделены шрифтом Courier New.
В некоторых заданиях решение требуется описать в виде процедуры или функции, что всегда оговаривается явно. В этом случае необходимо написать вызывающую программу, в которую включить описание требуемой подпрограммы и обращение к ней. Исходные данные и результаты задания должны быть объявлены параметрами процедуры или функции, а весь ввод-вывод организованы в основной программе.
Вычисление функций
1.1 Написать программу для вычисления и вывода таблицы значений заданной функции на интервале 1 £ x £ 10 c шагом h = 0,5
(задача табулирования функции):
y = 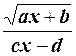
ProgramTab_Function;
Const
Xn = 1.0; {начальное значение аргумента}
Xk = 10.0; {конечное значение аргумента}
h = 0.5; {шаг изменения аргумента}
Var
a, b, c, d : Real;{параметры выражения}
x, y : Real; {аргумент и значение функции}
R, Q : Real; {подкоренное выражение и знаменатель}
Begin
Writeln('Введите параметры “a, b, c, d”');
Readln (a, b, c, d);
x := Xn;
while x <= Xk do
Begin
R := a * x + b;
Q := c * x - d;
{проверили существование функции}
if ( R > 0 ) And ( Q <> 0) then
Begin
y := Sqrt( R ) / Q;
Writeln('x=', x:4:1, ' y=', y:8:2)
End
Else
Writeln('x=', x:4:1, ' y- функция не существует');
x := x + h {изменили аргумент на шаг}
End
End.
Пояснения к программе
При вычислении функций в первую очередь необходимо обратить внимание на возможность возникновения ошибок времени выполнения из-за извлечения квадратного корня из отрицательного числа, деления на нуль, попытки вычисления элементарных математических функций вне области их определения и т.д. В данном примере в цикле проверяется знак подкоренного выражения и неравенство знаменателя нулю. И в том случае, если функцию вычислить невозможно, то выводится сообщение, что в данной точке значение функции не определено.
1.2 Протабулировать функцию на интервале –2 £ x £ 2 c шагом h = 0,4:
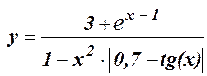
1.3 Протабулировать функцию на интервале 0 £ x £ 2,2 c шагом h = 0,4:
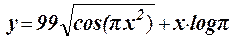
1.4 Протабулировать функцию на интервале - 0,2 £ x £ 0,8 c шагом h = 0,1:
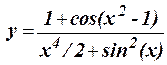
1.5 Протабулировать функцию на интервале -4 £ x < 4,5 c шагом h = 1:
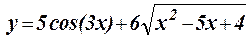
1.6 Протабулировать функцию на интервале -2p £ x £ 2p c шагом h = p/4:
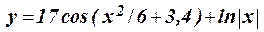
1.7 Протабулировать функцию на интервале 2 £ x £ 11 c шагом h = 1:
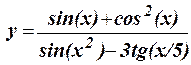
1.8 Протабулировать функцию на интервале 2,5 £ x £ 7,5 c шагом h = 0,25:
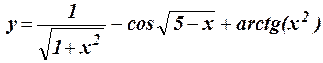
1.9 Протабулировать функцию на интервале 0,5 £ x £ 7 c шагом h = 0,35:
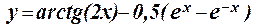
1.10 Протабулировать функцию на интервале 0,1 £ x £ 1,25 c шагом h = 0,1:
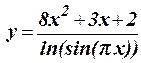
1.11 Протабулировать функцию на интервале 0,5 £ x £ 1,6 c шагом h = 0,1:
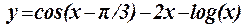
1.12 Протабулировать функцию на интервале -0,5£ x < 3,5 c шагом h = 0,5:
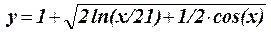
1.13 Протабулировать функцию на интервале 1£ x £ 10 c шагом h = 1:
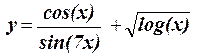
1.14 Протабулировать функцию на интервале 80 £ x £ 160 c шагом h = 20:
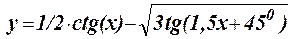
1.15 Протабулировать функцию на интервале 0,5£ x £ 3,75 c шагом h = 0,5:
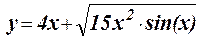
1.16 Протабулировать функцию на интервале –4 £ x £ –2,5 c шагом h = 0,1:
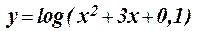
1.17 Протабулировать функцию на интервале 1 £ x £ 10 c шагом h = 1:
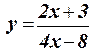
1.18 Протабулировать функцию на интервале -3/2p £ x £ 3/2p c шагом h=0,3:
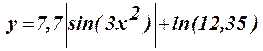
1.19 Протабулировать функцию на интервале -2p £ x £ 2p c шагом h = p/3:
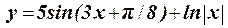
1.20 Протабулировать функцию на интервале 0,5 £ x £ 3,75 c шагом h = 0,5:
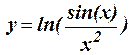
1.21 Протабулировать функцию на интервале -8 £ x < 8 c шагом h = 2,5:
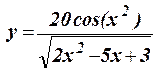
1.22 Протабулировать функцию на интервале -2p £ x £ 2p c шагом h = 0,8:
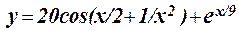
1.23 Протабулировать функцию на интервале -p/2 £ x £ p/2 c шагом h = 0,4:
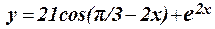
1.24 Протабулировать функцию на интервале 2 £ x < 11,5 c шагом h = 0,9:
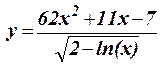
1.25 Протабулировать функцию на интервале 3 £ x £ 15 c шагом h = 1,5:
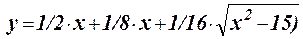
1.26 Протабулировать функцию на интервале 0,2 £ x £ 1,7 c шагом h = 0,2:
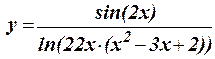
1.27 Протабулировать функцию на интервале 0,5 £ x < 9,5 c шагом h = 2,5:
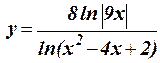
1.28 Протабулировать функцию на интервале 3 £ x £ 5,5 c шагом h = 0,3:
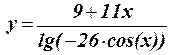
1.29 Протабулировать функцию на интервале 1,5£ x £ 12,5 c шагом h = 0,75:
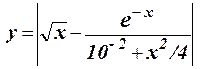
1.30 Составить программу для вычисления значения функции y =ex с помощью разложения функции в степенной ряд:
¥
ex = 1 + x + x2/2! + x3/3! + … + xn/n! + … = 1 + å xk/k!
k=1
с критерием остановки по заданной точности вычислений
½ xk/k! ½ £ e.
Пояснения к программе
Критерием окончания вычислений является заданная точность вычислений, поэтому число повторений цикла заранее неизвестно, процесс является итерационным и выход из цикла организуется по условию достижения требуемой точности. Вычислять каждый раз независимо степень xk и значение факториала k! нерационально, поэтому подсчет очередного члена ряда осуществляется через предыдущее значение по формуле
rk = rk-1 x / k .
program Iterative (input, output);
{ вычисление функции с помощью степенного ряда }
Var
Eps : Real; { точность вычислений }
X : Real; { аргумент }
R : Real; { очередной член ряда }
V : Real; { значение степенного ряда }
k : Integer; { счетчик членов ряда }
Begin
Writeln ('Введите точность вычислении');
Readln (Eps);
Writeln ('Введите аргумент');
Readln (X);
{ задание начального значения переменных цикла }
k := 1;
Y := 1;
R := X;
while abs(R) > Eps do
Begin
У := У + R;
k := k + 1;
R := R * X / k
End;
Writeln (' X =',Х:5:2,' ':5,'У = ', У + R:8:3)
End.
1.31 Составить программу для вычисления значения функции y =e-x с помощью разложения функции в степенной ряд (см. п. 1.30):
e-x = 1 – x/1! + x2/2! – x3/3! + … + (–1)n xn/n! + … .
1.32 Составить программу для вычисления значения функции y =sin(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
sin(x) = x – x3/3! + x5/5! – x7/7! + … + (-1)n x2n+1/(2n+1)! + … .
1.33 Составить программу для вычисления значения функции y =cos (x) с помощью разложения функции в степенной ряд (см. п. 1.30):
cos(x) = 1 – x2/2! + x4/4! – x6/6! + … + (–1)n x2n/(2n)! + … .
1.34 Составить программу для вычисления значения функции y =sh(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
sh(x) = x + x3/3! + x5/5! + x7/7! + … + x2n+1/(2n+1)! + … .
1.35 Составить программу для вычисления значения функции y =ch(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
ch(x) = 1 + x2/2! + x4/4! + x6/6! + … + x2n/(2n)! + … .
1.36 Составить программу для вычисления значения функции y =ln(1+x) с помощью разложения функции в степенной ряд (см. п. 1.30):
ln(1+x) = x/1 – x2/2 + x3/3 - x4/4 +… + (–1)n+1 xn/n + … .
1.37 Составить программу для вычисления значения функции y =ln(1-x) с помощью разложения функции в степенной ряд (см. п. 1.30):
ln(1-x) = – x/1 – x2/2 – x3/3 – x4/4–… – xn/n + … .
1.38 Составить программу для вычисления значения функции 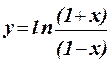 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
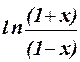 = 2( x/1 + x3/3 + x5/5 + x7/7 +… + x2n+1/(2n+1) + …) .
= 2( x/1 + x3/3 + x5/5 + x7/7 +… + x2n+1/(2n+1) + …) .
1.39 Составить программу для вычисления значения функции y =1/(1+x) с помощью разложения функции в степенной ряд (см. п. 1.30):
1/(1+x) = 1 – x + x2 – x3 + x4 -… + (–1)n xn + … .
1.40 Составить программу для вычисления значения функции y =1/(1+x)2 с помощью разложения функции в степенной ряд (см. п. 1.30):
1/(1+x)2 = 1 – 2x + 3x2 – 4x3 + 5x4–… + (–1)n (n+1)xn + … .
1.41 Составить программу для вычисления значения функции y =1/(1+x)3 с помощью разложения функции в степенной ряд (см. п. 1.30):
1/(1+x)3 = 1 – 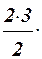 x +
x + 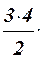 x2 –
x2 – 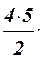 x3 + … +
x3 + … + 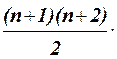 xn +….
xn +….
1.42 Составить программу для вычисления значения функции 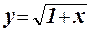 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
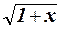 = 1 +
= 1 + 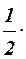 x –
x – 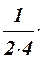 x2 +
x2 + 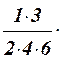 x3 – … .
x3 – … .
1.43 Составить программу для вычисления значения функции 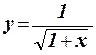 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
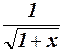 = 1 –
= 1 – 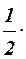 x +
x + 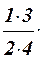 x2 –
x2 – 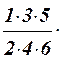 x3 + … .
x3 + … .
1.44 Составить программу для вычисления значения функции 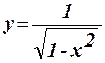 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
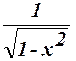 = 1 +
= 1 + 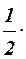 x2 +
x2 + 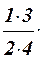 x4 +
x4 + 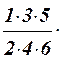 x6 + … .
x6 + … .
1.45 Составить программу для вычисления значения функции 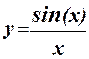 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
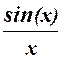 = 1 – x2/3! + x4/5! – x6/7! + … + (–1)n x2n/(2n+1)! + … .
= 1 – x2/3! + x4/5! – x6/7! + … + (–1)n x2n/(2n+1)! + … .
1.46 Составить программу для вычисления значения функции 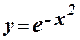 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
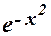 = 1 – x2/1! + x4/2! – x6/3! + … + (–1)n x2n/n! + … .
= 1 – x2/1! + x4/2! – x6/3! + … + (–1)n x2n/n! + … .
1.47 Составить программу для вычисления значения функции y =arctg(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
arctg(x) = x – x3/3 + x5/5 – x7/7 + … + (–1)n x2n+1/(2n+1) + … .
1.48 Составить программу для вычисления значения функции y =arcsin(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
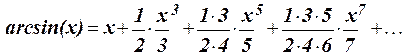
1.49 Составить программу для вычисления функции y = 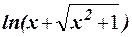 с помощью разложения функции в степенной ряд (см. п. 1.30):
с помощью разложения функции в степенной ряд (см. п. 1.30):
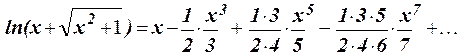
Одномерные массивы
2.1 Составить программу вычисления значения полинома n-ой степени:
y = a0 xn + a1 xn-1 + … + an-1 x + an .
Для вычисления полинома удобно использовать формулу Горнера (гнездовую процедуру)
y = (…( (a0 x + a1 ) x + a2 ) x + … + an-1 ) x + an .
Если выражение, стоящее внутри скобок, обозначить y i, то значение выражения в следующих скобках можно вычислить, используя рекуррентную формулу
yi+1 = yi x + an-1.
Значение полинома yполучается после повторения этого процесса в цикле nраз. Начальное значение yiцелесообразно взять равным a0, а цикл начинать с i = 1. Все коэффициенты полинома и свободный член, как правило, сводятся в массив, состоящий из элементов n + 1(n — порядок полинома).
program GORNER (Input, output);
{ вычисление значения полинома по схеме Горнера }
Var
I, N : Integer; { параметр цикла и степень полинома }
X, Y : Real; { аргумент и значение полинома }
А : Array[0..100] of Real;{массив коэффициентов полинома}
Begin
{ Ввод исходных данных }
Writeln ( ’Введите порядок полинома N < 100’ );
Readln ( N );
Writeln (’Введите аргумент’);
Readin ( X );
Writeln (’Введите коэффициенты полинома, ’);
Writeln (’начиная с коэффициента при старшей степени’);
for i := 0 to N do
Read ( A[i] );
Y := A[0];
for i := 1 to N do
Y := Y*X + A[i];
{ вывод результата }
Writeln ('Значение полинома =', Y:10:2)
End.
2.2 Заданы два вектора X = { xi } и Y = { yi }, i = 1 ¸ n. Написать программу формирования третьего вектора Z = { zi }, каждый элемент которого zi = max ( xi, yi ).
2.3 Задана последовательность величин x1, x2, ..., xn. Написать программу вычисления суммы элементов из указанной последовательности, удовлетворяющих неравенству xk > р, где р заданная величина.
2.4 Написать программу вычисления скалярного произведения двух векторов
_ _ n
( a, b) = å ai bi .
i=1
2.5 Пусть дано натуральное число пи вещественные числа а1, а2, ..., аn. В последовательности а1, а2, ..., аn все отрицательные члены увеличить на 0,5, а все неотрицательные, меньшие среднего арифметического, заменить на 0,1.
2.6 Пусть даны натуральное число п, целые числа а1, а2, ..., аn. Получить сумму положительных, число отрицательных и число нулевых членов последовательности а1, а2, ..., аn..
2.7 Пусть даны целые числа а1 , а2 , ..., аn , b1 , b2 , ..., bn . Преобразовать последовательность b1, b2, ..., bnпо правилу, согласно которому если аi £0, тоbi увеличивается в 10 раз, иначе bi, заменяется нулем (i = 1,..., n).
2.8 С помощью следующего фрагмента программы вычислить сумму тех элементов массива х, индексы которых совпадают со значениями элементов массива а (аi ¹ аj при i ¹ j).
Var
x: аrrау [1..100] of real:
а: аrrау [1..30] of 1..100;
2.9 Пусть даны целые числа а1, а2, ..., аn , каждое из которых отлично от нуля. Если в последовательности отрицательные и положительные члены чередуются, то ответом должна служить сама исходная последовательность. Иначе — получите все отрицательные члены последовательности, сохранив порядок их следования.
2.10 Пусть дано натуральное число пи вещественные числа а1, а2, ..., аn. Найти максимальное значение в массиве A и его индекс.
program Maximum ( Input, Output );
Const
MinIndex = 1; MaxIndex = 10;
Type
Index = MinIndex .. MaxIndex;
Massiv = Array [ Index ] of Real;
Var
i, K : Index;
Max : Real;
A : Massiv;
Begin
Writeln ('Введите элементы массива "A"');
for i := MinIndex to MaxIndex do
Read ( A[ i ] );
Max := A[ MinIndex ]; K := MinIndex;
for i := MinIndex + 1 to MaxIndex do
if A[ i ] > Max then
Begin Max := A[ i ]; K := i end;
Write ('Максимумом явл-ся',K:3,' элемент массива "А"');
Writeln (', его значение =', Max:6:2)
End.
2.11 Пусть даны вещественные числа а1, а2, ..., аn.Требуется умножить все члены последовательности а1, а2, ..., аn на квадрат ее наименьшего члена, если аi ³ 0, и на квадрат ее наибольшего члена, если аi < 0.
2.12 Пусть даны целые числа а1, а2, ..., аn . Получите новую последовательность, выбросив из исходной максимальный и минимальный члены.
2.13 Пусть дана последовательность из 100 различных целых чисел. Найдите среднее арифметическое чисел этой последовательности, расположенных между максимальным и минимальным числами (в сумму включить и оба этих числа).
2.14 Используя следующий фрагмент программы, преобразуйте массив x по указанному ниже правилу, воспользовавшись массивом y как вспомогательным:
Var
х, у: array [1..70] ofreal;
k: 1..69;
а) все отрицательные элементы массива x перенесите в его начало, а все остальные — в конец, сохраняя исходное взаимное расположение как среди отрицательных, так и среди остальных элементов;
б) элементы массива х циклически сдвиньте на k позиций влево.
2.15 Пусть элементы из массива х упорядочены по неубыванию, а элементы массива у — по невозрастанию. Используя следующий фрагмент программы, объедините элементы этих двух массивов в один массив z так, чтобы они оказались упорядоченными по неубыванию:
Const
k = 10:
m = 20;
n = k + m;
Var
x : array[ 1..k ] of real;
у : array[ 1..m ] of real;
z : array[ 1..n ] of real;
2.16 Пусть даны вещественные числа а1 , а2 , ..., а 2n . Получите:
а) max( а1 + а2n , а2 + а2n - 1 , ..., аn + а n +1 ) ;
б) min( а1 а n+1 , а2 а n+2 , ... , аn а 2n ) .
2.17 Пусть даны вещественные числа а1, а2, ..., а 20. Преобразуйте последовательность по правилу: большее из а iи а i+10 (i = 1,...,10) примите в качестве нового значения а i, меньшее — в качестве нового значения а i+10.
2.18 Пусть даны целые числа а1 , а2 , ..., а n. Если в данной последовательности ни одно четное число не расположено после нечетного, то получите все отрицательные члены последовательности, иначе — все положительные. Порядок следования чисел в обоих случаях замените обратным.
2.19 Пусть дан фрагмент программы:
Var
k : 0 .. 9999:
d : array [ 1..4 ] of '0' .. '9';
а) запишите в массив d цифры числа k;
б) получите целое k, составленное из цифр массива d.
2.20 В массиве из 20 целых чисел найдите наибольший элемент среди отрицательных (считайте, что такой элемент один) и поменяйте его местами с первым элементом.
2.21 Пусть даны натуральные числа п, а1 , а2 , ..., а n . Определите количество членов а i последовательности а1 , а2 , ..., а n :
а) являющихся нечетными числами;
б) кратных 3 и не кратных 5;
в) являющихся квадратами четных чисел;
г) удовлетворяющих условию: а i < (а i + а i+1)/2;
2.22 Составить программу для подсчета числа компонент логического вектора В = { bi }, i= 1 ¸ n, имеющих значение false.
2.23 Составить программу формирования из вектора A = { ai }, i= 1 ¸ 3n вектора В = { bi }, i= 1 ¸ n, очередная компонента которого равна среднему арифметическому очередной тройки компонент вектора А.
2.24 Составить программу осуществления циклического сдвига влево на одну позицию компонент вектора В = { bi }, i= 1 ¸ n.
2.25 Составить программу присвоения логической переменной Aзначения true, если элементы вещественного вектора В = { bi }, i= 1 ¸ nобразуют неубывающую последовательность (b1 ≤ b2 ≤ ... ≤ bn) и значение false — в противном случае.
2.26 Задан вектор A = { ai }, i= 1 ¸ n. Составить программу для формирования нового вектора A = { ai }, i= 1 ¸ n-1, получаемого из вектора Апутем исключения минимального элемента (с сохранением порядка расположения оставшихся элементов).
2.27 Составить программу преобразования вектора A = { ai }, i= 1 ¸ n так, чтобы его компоненты располагались в обратном порядке, т.е. получить вектор A = { an , an-1,…, a1 }.
2.28 Составить программу подсчета у логического вектора В = { bi }, i= 1 ¸ nмаксимального количества стоящих подряд компонент с значением false.
2.29 Задан вектор В = { bi }, i= 1 ¸ n. Составить программу вычисления наибольшего и наименьшего значения модуля разности между соседними элементами.
2.30 Составить программу объединения двух упорядоченных последовательностей чисел a1 ≤ a2 ≤ ... ≤ an и b1 ≤ b2 ≤ ... ≤ bm в одну упорядоченную последовательность.
2.31 Пусть даны вещественные числа а1 , а2 , ..., аn , b1 , b2 , ..., bn . Вычислите произведение ( а1 + bn ) ( а2 + bn -1 )...( аn + b1 ).
2.32 Используя следующий фрагмент, напишите программы для решения перечисленных ниже задач:
Const
n = 20;
Var
x: array [1..n] of integer;
y, k : integer; t: Boolean;
а) переменной t присвоить значение true, если элементы массива x упорядочены по возрастанию, иначе значение false;
б) переменной t присвоить значение true, если в массиве x нет нулевых элементов и при этом положительные элементы чередуются с отрицательными, иначе значение false;
в) переменной k присвоить либо номер первого вхождения у в массив х, либо число n+1, если у не входит в х;
г) вычислить y = x1 + x1х2 + x1х2х3 + ... + x1х2...х т, где т — либо номер первого отрицательного элемента массива х, либо число n, если в массиве x нет отрицательных элементов.
2.33 Пусть дан массив из n элементов. Каждый отрицательный элемент замените полусуммой тех двух элементов, которые стоят рядом с ним справа и слева.
2.34 Пусть дана последовательность из n элементов. Уменьшите ее, удалив первый из отрицательных и минимальный из положительных (считайте, что такой элемент один) и сдвинув все остальные к началу.
2.35 Пусть дана последовательность из n элементов. Уменьшите ее, удалив все минимальные и максимальные элементы и сдвинув все остальные к началу последовательности.
2.36 Замените каждый элемент массива средним арифметическим всех предшествующих ему элементов.
2.37 Пусть даны вещественные числа а1 , а2 , ..., а n. Получите числа b1 , b2 , ..., bn, где b i — среднее арифметическое всех членов последовательности а1 , а2 , ..., а n, кроме а i (i =1,..., n).
2.38 Используя следующий фрагмент программы, упорядочьте массив x по неубыванию (то есть переставьте его элементы так, чтобы для всех i выполнялось условие хi£ хi+1) в соответствии с перечисленными ниже алгоритмами сортировки (упорядочения):
Const
n = 20;
Var
x : array [1..n] of real;
а) сортировка выбором — отыскивается максимальный элемент и переносится в конец массива; затем этот метод применяется ко всем элементам, кроме последнего (он уже находится на своем месте), и
т. д.;
б) сортировка обменом (пузырьковая сортировка) — последовательно сравниваются пары соседних элементов хi≤ хi+1 (i = 1, 2, ..., n-1), и если хi > хi+1 то они переставляются; тем самым наибольший элемент оказывается на своем месте в конце массива; затем этот метод применяется ко всем элементам, кроме последнего, и т. д.;
в) сортировка вставками — пусть первые kэлементов массива уже упорядочены по неубыванию; берется (k+1)-й элемент и размещается среди первых k элементов так, чтобы упорядоченными оказались уже k+1первых элементов; этот метод применяется при k от 1 до п - 1.
2.39 Пусть элементы массива х упорядочены по возрастанию. С помощью представленного ниже фрагмента программы присвойте переменной k номер элемента массива х, равного числу y, или 0, если такого элемента нет. При этом использовать следующий метод двоичного (бинарного) поиска: сравнить y со средним элементом массива (или элементом около середины); если эти числа равны, поиск завершается, если же y меньше среднего элемента, то y надо искать в левой половине массива, а иначе — в правой. Далее к выбранной половине применяется этот же алгоритм.
2.40 Пусть даны две последовательности по n целых чисел в каждой. Найдите наименьшее среди тех чисел первой последовательности, которые не входят во вторую последовательность, считая, что хотя бы одно такое число есть.
2.41 Пусть дана последовательность из n целых чисел. Определите количество инверсий в этой последовательности (то есть таких пар элементов, в которых большее число находится слева от меньшего: х i >хj при i< j).
2.42 Пусть даны вещественные числа а1 , а2 , ..., аn . Если в результате замены отрицательных членов последовательности а1 , а2 , ..., аn их квадратами члены будут образовывать неубывающую последовательность, то получите сумму членов исходной последовательности; в противном случае получите их произведение.
2.43 Пусть даны целые числа а1 , а2 , ..., аn . Пусть М— наибольшее, т — наименьшее из них. Получите в порядке возрастания все целые числа из интервала (т, М), которые не входят в последовательность а1, а2, ..., аn.
2.44 Присвойте переменной f значение true, если в некотором массиве нет нулевых элементов и при этом положительные элементы чередуются с отрицательными, в противном случае присвойте значение false.
2.45 Пусть даны натуральное число п, целые числа а, х1, х2,..., хп. Если в последовательностих1, х2, ..., хп есть хотя бы один член, равный а, то получите сумму всех членов, следующих за первым таким членом, иначе найдите минимальный среди нечетных чисел последовательности
х1, х2, ..., хп.
2.46 Пусть даны целые числа а1, а2, ..., аn, среди которых могут быть повторяющиеся. Составьте новый массив из чисел, которые входят в последовательность по одному разу.
2.47 Пусть даны целые числа а1, а2, ..., аn,среди которых могут быть повторяющиеся. Составьте новый массив из чисел, взятых по одному из каждой группы равных членов данной последовательности.
2.48 Пусть даны натуральные числа k, п, вещественные числаа1, а2, ..., аk n. Получите последовательность max(а1, а2, ..., аk), max(аk+1, аk+2, ..., а2k),..., max(аk(n-1)+1, ..., аk n).
2.49 В массиве из пэлементов подсчитайте количество четверок аi, аi+1, аi+2, аi+3, идущих подряд членов, из которых:
а) все члены равны;
б) все члены различны.
2.50 Пусть дан фрагмент программы:
Var
k : 0 .. 9999:
d : array [ 1..4 ] of '0' .. '9';
а) запишите в массив d цифры числа k;
б) получите целое k, составленное из цифр массива d.
Матрицы
3.1 Составить программу транспонирования квадратной матрицы.
3.2 Задана вещественная матрица A = { ai j }, i= 1 ¸ n, j= 1 ¸ m. Составить программу формирования новой матрицы B = { bij }, i= 1 ¸ n, j= 1 ¸ m, каждая строка которой должна быть получена из соответствующей строки матрицы Aпутем упорядочения ее элементов в порядке убывания.
3.3 Составить программу построения по прямоугольной вещественной матрице A = { aij }, i= 1 ¸ n, j= 1 ¸ m логического вектора В = { bi }, i= 1 ¸
|
из
5.00
|
Обсуждение в статье: Перечисляемый и диапазонный типы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

