Определение закона распределения результатов измерений или случайных погрешностей измерений

Лекция 8 ОБРАБОТКА РЕЗУЛЬТАТОВ прямых ИЗМЕРЕНИЙ

Прямые многократные измерения

Прямые многократные измерения делятся на равно- и неравно­точные. Равно­точными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех рядов измерений равны между собой.

Перед проведением обработки результатов измерений необхо­димо удостовериться в том, что данные из обрабатываемой выбор­ки статистически подконтрольны, группируются вокруг одного и того же центра и имеют одинаковую дисперсию.

Задача обработки результатов многократных измерений за­ключается в нахождении оценки измеряемой величины и довери­тельного интервала, в котором находится ее истинное значение.

Исходной информацией для обработки является ряд из n (n >4) результатов измерений х₁, х₂, x₃,..., х_n, из которых исключены известные систематические погрешности, – выборка. Число n за­висит как от требований к точности получаемого результата, так и от реальной возможности выполнять повторные измерения.

Последовательность обработки результатов прямых многократ­ных измерений состоит из ряда этапов:

1 Определение точечных оценок закона распределения резуль­татов измерений.На этом этапе определяются:

• среднее арифметическое значение 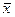измеряемой величины

;

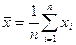• СКО результата измерения S_x

;

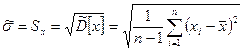• СКО среднего арифметического значения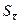

.

В соответствии с критериями, рассмотренными в лекции 6, грубые погрешности и промахи исключаются, после чего проводится по­вторный расчет оценок среднего арифметического значения и его СКО. В ряде случаев для более надежной идентификации закона распределения результатов измерений могут определяться другие точечные оценки: коэффициент асимметрии, эксцесс и контрэкс­цесс, энтропийный коэффициент.

Определение закона распределения результатов измерений или случайных погрешностей измерений.

Первым шагом при идентификации закона распределения яв­ляется построение по исправленным результатам измерений х_i, где i = 1, 2,..., n, вариационного ряда (упорядоченной выборки), а также у_i, где у₁ = min(х_i) и у_n= mах(x_i). В вариационном ряду результаты измерений (или их отклонения от среднего арифмети­ческого) располагают в порядке возрастания. Далее этот ряд раз­бивается на оптимальное число m, как правило, одинаковых интервалов группирования длиной h = (у₁ + у_n)/m .

Оптимальным является такое число интервалов m, при котором возможное максимальное сглаживание случайных флуктуации дан­ных сопровождается с минимальным искажением от сглаживания самой кривой искомого распределения. Для практического приме­нения целесообразно использовать выражения m_min = 0.55n^0,4 и m_max = 1.25n^0,4,

которые получены для наиболее часто встречающихся на практике распределений с эксцессом, на­ходящимся в пределах от 1,8 до 6, т.е. от равномерного до распре­деления Лапласа.

Искомое значение m должно находится в пределах от m_min до m_mах, быть нечетным, так как при четном m в островершинном или двухнедельном симметричном распределении в центре гисто­граммы оказываются два равных по высоте столбца и середина кривой распределения искусственно уплощается.

В случае если гистограмма распределения явно двухмодальная, число столбцов может быть увеличено в 1,5 - 2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. Полученное значение длины интервала группирования h всегда округляют в большую сторону, иначе последняя точка окажется за пределами крайнего интервала.

Далее определяют интервалы группирования экспериментальных данных в виде

Δ₁ = (y₁, y₁+h); Δ₂ = (y₁+h, y₁+2h);....; Δ_n = (y_n–h, y_n),

и подсчитывают число попаданий n_k (частоты.) результатов измере­ний в каждый интервал группирования. Сумма этих чисел должна равняться числу измерений. По полученным значениям рассчиты­вают вероятности попадания результатов измерений (частности) в каждый из интервалов группирования по формуле 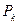= P_k/Δ_k, где k=1, 2,...,m.

Проведенные расчеты позволяют построить гистограмму, по­лигон и кумулятивную кривую.

Для построения гистограммыпо оси результатов наблюдений х (рисунок 8.1,а) откладываются интерва­лы Δ_k в порядке возрастания номеров и на каждом интервале стро­ится прямоугольник высотой P_k. Площадь, заключенная под графи­ком, пропорциональна числу наблюдений n. Иногда высоту прямоугольника откладывают равной эмпирической плотности ве­роятности 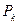= P_k/Δ_k = n_k/(nΔ_k), которая является оценкой сред­ней плотности в интервале Δ_k. В этом случае площадь под гисто­граммой равна единице. При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более при­ближается к гладкой кривой – графику плотности распределения вероятности.

Полигонпредставляет собой ломаную кривую, соединяющую середины верхних оснований каждого столбца гистограммы (смотри рисунок 8.1,а). Он более наглядно, чем гистограмма, отражает форму кривой распределения. За пределами гистограммы справа и слева остаются пустые интервалы, в которых точки, соответствующие их серединам, лежат на оси абсцисс. Эти точки при построении полигона соединяют между собой отрезками прямых линий. В результате совместно с осью х образу­ется замкнутая фигура, площадь которой в соответствии с прави­лом нормирования должна быть равна единице (или числу на­блюдений при исполь­зовании частостей).

Кумулятивная кривая– это график статистической функ­ции распределения. Для ее построения по оси результатов наблю­дений х (рисунок 8.1,б) от­кладывают интервалы Δ_k в порядке возраста­ния номеров и на каж­дом интервале строят прямоугольник высо­той

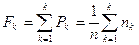
Значение F_k называ­ется кумулятивной частностью, а сумма n_k – кумулятивной частотой.

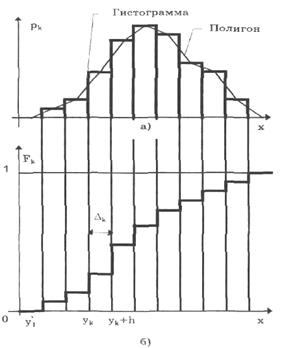
Рисунок 8.1 – Гистограмма, полигон (а) и кумулятивная кривая (б).

По виду построения зависимостей может быть оценен за­кон распределения результатов измерений.

3 Статистические критерии оценки нормальности распределения.В качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения используются критерии согласия. Известен целый ряд критериев согласия, предложенных разными авторами. Наибольшее распространение в практике получил критерий Пирсона (критерий хи–квадрат). Идея этого метода состоит в контроле отклонений гистограм­мы экспериментальных данных от гистограммы с таким же чис­лом интервалов, построенной на основе распределения, совпадение с которым определяется. Использование критерия Пирсона возможно при большом числе измерений (n > 50) и заключается в вычислении величины 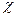² (хи – квадрат):

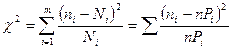(8.1)

где n_j, N_j – экспериментальные и теоретические значения частот в i-м интервале разбиения; m – число интервалов разбиения; Р_i – значения вероятностей в том же интервале разбиения, соот­ветствующие выбранной модели распределения;

При n → ∞ случайная величина 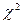имеет распределение .Пирсо­на с числом степеней свободы v = m–1–r, где r – число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы. Для нормального закона распределения r = 2, так как закон однозначно характеризуется указанием двух его параметров – математического ожидания и СКО.

Если бы выбранная модель в центрах всех т столбцов совпадала с экспериментальными данными, то все т разностей (n_i – N_i) были бы равны нулю, а, следовательно, и значение критерия 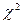также было бы равно нулю. Таким образом, 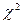есть мера суммарного от­клонения между моделью и экспериментальным распределением.

Критерий 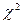не инвариантен к числу столбцов и существенно возрастает с увеличением их числа. Поэтому для использования его при разном числе столбцов составлены таблицы квантилей распре­деления 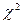входом, в которые служит так называемое число степе­ней свободы v = (m–1–r). Чтобы совместить модель, соответствую­щую нормальному закону, с гистограммой, необходимо совместить координату центра, а для того, чтобы ширина модели соответст­вовала ширине гистограммы, ее нужно задать как r = 2 и v = m–3. Часть квантилей распределения 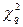приведена в таблице 8.1.

Таблица 8.1

Значения 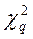при различном уровне значимости

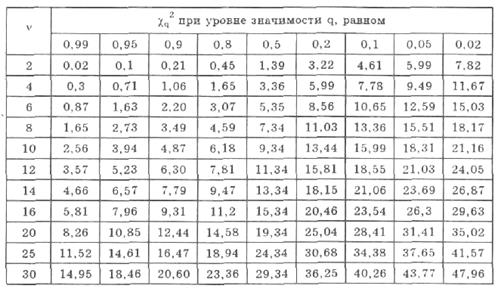
Если вычисленная по опытным данным мера расхождения 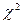меньше определенного из таблицы значения 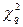. то гипотеза о сов­падении экспериментального и выбранного теоретического распре­делений принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. она не противоречит опытным данным. Если же 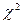выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.

Методика определения соответствия экспериментального и принятого законов распределения заключается в следующем:

• определяют оценки среднего арифметического значения 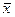и СКО ;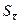

• группируют результаты многократных наблюдений по интер­валам длиной h, число которых определяют так же, как и при построении гистограммы;

• для каждого интервала разбиения определяют его центр х_i0 и подсчитывают число наблюдений n_i, попавших в каждый интервал;

• вычисляют число наблюдений для каждого из интервалов, теоретически соответствующее выбранной аналитической модели распределения. Для этого сначала от реальных середин интервалов х_i0 производят переходи нормированным серединам

z_i = (х_i0 – 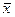)/S_х .

Затем для каждого значения z_i, с помощью аналитической модели находят значение функции плотности вероятностей f(z_i). Например, для нормального закона

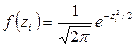
По найденному значению f(z_i) определяют ту часть N_i, имею­щихся наблюдений, которая теоретически должна быть в каждом из интервалов N_i=nh f(z_i)/S_х, где n – общее число наблюдений;

• если в какой-либо интервал теоретически попадает меньше пяти наблюдений, то в обеих гистограммах его соединяют с сосед­ним интервалом. После этого определяют число степеней свободы v = m–1–r, где m – общее число интервалов. Если было произве­дено укрупнение, то m – число интервалов после укрупнения;

• по формуле (8.1) определяют показатель разности частот ;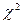

• выбирают уровень значимости критерия q. Он должен быть небольшим, чтобы была мала вероятность, совершить ошибку пер­вого рода. По уровню значимости и числу степеней свободы v по табл. 8.1 находят границу критической области 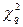такую, что

Р{ 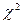> 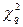} = q.

Вероятность того, что полученное значение 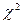превыша­ет 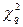, равна q и мала. Поэтому, если оказывается, что 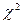> 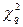, то гипотеза о совпадении экспериментального и теоретического законов рас­пределения отвергается. Если же 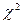< 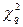, то гипотеза принимается.

Чем меньше q, тем больше значение 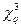(при том же числе сте­пеней свободы v), тем легче выполняется условие 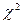< 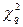и прини­мается проверяемая гипотеза. Но при этом увеличивается вероят­ность ошибки второго рода. В связи с этим нецелесообразно при­нимать 0,02 q 0,01.

Иногда вместо проверки с односторонней критической областью при­меняют проверки с двусторонними критическими областями. При этом оценивается вероятность Р{ 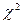> 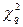} = q Уровень значимо­сти критерия q делится на две части: q = q₁+q₂. Как правило, прини­мают q₁=q₂. По табл. 8.1 для Р{ 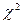> 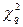}=0 находят 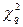при уровне значимости q₁ и числе степеней свободы v и 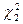для уровня значи­мости 1 – q₂ и том же n. Гипотеза о совпадении распределений принимается, если .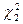

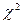
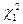При n <15 принадлежность экспериментального распределения к нормальному не проверяется.

4 Определение доверительных границ случайной погрешности.Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множи­тель z_Р при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности Δ = ± z_{p .}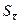

5 Определение границ не исключенной систематической погреш­ности θ результата измерений.Под этими границами понимают найденные нестатистическими методами границы интервала, внут­ри которого находится неисключенная систематическая погрешность. Она образуется из ряда составляющих: как правило, погрешностей метода и средств измерений, а также субъективной погрешности. Границы неисключенной систематической погрешности принима­ются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы. Они суммируются по правилам, которые будут рассмотрены нами позже. Доверительная вероятность при определении гра­ниц θ принимается равной доверительной вероятности, используе­мой при нахождении границ случайной погрешности.

6 Определение доверительных границ погрешности результа­та измерения Δ_р. Данная операция осуществляется путем сумми­рования СКО случайной составляющей 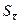и границ неисключен­ной систематической составляющей в θ зависимости от соотношения θ/ 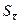по правилам, которые будут рассмотрены в лекции 10

7 Запись результата измерения.Результат измерения записы­вается в виде

х = 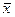± Δ_Р

при доверительной вероятности Р = Р_д. При отсутствии данных о виде функции распределения составляю­щих погрешности результаты измерений представляют в виде 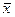, , 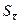n, θ при доверительной вероятности Р = Р_д.