 |
Главная |
Команда «Подбор параметров»
|
из
5.00
|
для нахождения значения, приводящего к требуемому результату
Основной командой для решения оптимизационных задач в Excel является команда Сервис/Подбор параметра. Эта команда определяет неизвестную величину, приводящую к требуемому результату.
Для работы с командой Подбор параметра необходимо подготовить лист, чтобы в листе находились:
• формула для расчета;
• пустая ячейка для искомого значения;
• другие величины, которые используются в формуле.
Ссылка на пустую ячейку должна обязательно присутствовать в формуле, так как именно она является переменной, значение которой ищет Excel. Во время подбора параметра в переменную ячейку непрерывно заносятся новые значения, пока не будет найдено решение поставленной задачи.
Такой процесс называется итерацией, и продолжается он до тех пор, пока редактор не выполнит 100 попыток или не найдет решения, лежащее в пределах точности 0,001 от точного значения (настройка этих параметров осуществляется с помощью команды Сервис/Параметры, вкладка Вычисления)
Этапы оптимизации :
Создайте лист, например, с формулой =B1*B2 в ячейке B3, пустой (переменной) ячейкой (B2) и другими данными (B1), которые могут понадобиться при вычислениях. Например, необходимо определить количество книг по цене 23,75 грн., которые необходимо продать, чтобы объем продаж составил 10000,00 грн.

2/Выделите ячейку листа (B3), в которой содержится формула (эта ячейка появится в поле "Установить в ячейке" в окне диалога Подбор параметра). Выполните команду Сервис/Подбор параметра. Открывается окно диалога Подбор параметра..
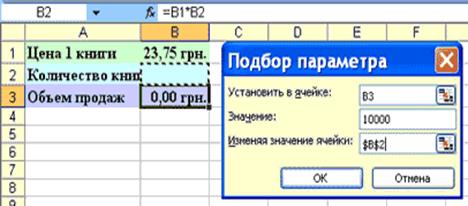
3/ Введите в текстовое поле Значение число, соответствующее объему продаж - 10000. Переместите курсор в текстовом поле Изменяя значения ячейки. Выделите ту ячейку, в которой должен содержаться ответ (переменная ячейка). Ее содержимое будет подобрано и подставлено в формулу командой Подбор параметра. Выделенная ячейка (B2) выделяется на листе рамкой. Нажмите кнопку ОК, чтобы найти решение.
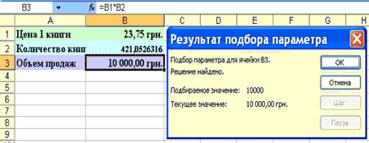
После завершения итерационного цикла в окне диалога Результат подбора параметра появляется сообщение, а результат заносится в ячейку листа. Решение показывает, что для достижения объема продаж 10000 грн. необходимо продать 421 книгу по цене 23,75 грн. Для закрытия окна диалога Результат подбора параметра щелкните на кнопке ОК.
Контрольные вопросы:
- что такое симплекс метод
- что такое целевая ячейка
- какого рода задачи решаются с помощью инструмента «Поиск решения»
- как установить нужные ограничения в окне «Поиск решения»
Теория
Общая задача линейного программирования решается симплексным методом
Симплекс(лат. simplex - простой) – простейший выпуклый многогранник
в n-мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве)

На рисунке: оптимальное решение находится в одной из вершин многоугольника решений А, В, С, D
Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точкемногогранника решений (и совпадает с одним из допустимых базисных решений системы ограничений)
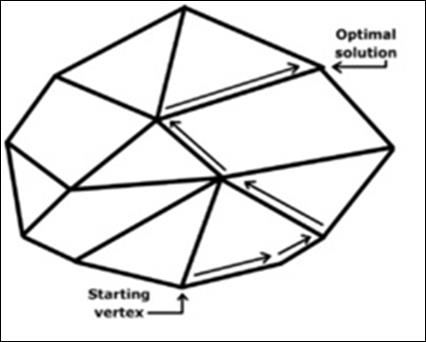

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (по крайней мере, не худшее) значение
Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949
Джордж Бернард Данциг(1914-2005) – американский математик, разработал симплексный алгоритм, считается основоположником методов линейного программирования
Идеи симплексного метода были разработаны в 1939 г. российским ученым Л.В.Канторовичем
Леонид Витальевич Канторович(1912-1986) – советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Один из создателей линейного программирования
|
из
5.00
|
Обсуждение в статье: Команда «Подбор параметров» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

