Нестандартные задачи как средство развития логического мышления

Лябина Т.И.

Учитель математики высшей категории

МОУ «Мошокская средняя общеобразовательная школа»

 

Нестандартные задачи как средство развития логического мышления

Какая задача по математике может называться нестандартной? Хорошее определение приведено в книге

« Как научиться решать задачи» авторов Л.М. Фридмана, Е.Н. Турецкого.

-Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Не следует путать их с задачами повышенной сложности. Условия задач повышенной сложности таковы, что позволяют ученикам довольно легко выделить тот математический аппарат, который нужен для решения задачи по математике. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач этого типа. А вот нестандартная задача предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого – решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 5 классе нестандартна, а в 6 классе она является обычной, и даже не повышенной сложности.

Итак, если решение задачи учащийся не знает, на какой теоретический материал ему опираться, он тоже не знает, то в этом случае задачу по математике можно назвать нестандартной на данный период времени.

Каковы же методы обучения решению задач по математике, которые мы считаем на данный момент нестандартными? Универсального рецепта, к сожалению, никто не придумал, учитывая уникальность данных задач. Некоторые учителя, что называется, натаскивают в шаблонных упражнениях. Происходит это следующим образом: учитель показывает способ решения, а затем ученик повторяет это при решении задач многократно. При этом убивается интерес учащихся к математике, что, по меньшей мере, печально.

Научить ребят решению задач нестандартного вида можно, если вызвать интерес, другими словами, предложить задачи, интересные и содержательные для современного ученика. Или же заменять формулировку вопроса, используя проблемные жизненные ситуации. Например, вместо задания «решить Диафантово уравнение», предложить решить следующую задачу. Может ли

ученик расплатиться за покупку стоимостью 19 р., если у него только трехрублевые купюры, а у продавца – десятирублевые?

Также действенен метод подбора вспомогательных задач. Это средство обучения решению задач говорит об определенном уровне достижения в решении задач. Обычно в таких случаях думающий ученик пытается самостоятельно, без помощи учителя находить вспомогательные задачи или упрощать и видоизменять условия данных задач.

Умение решать нестандартные задачи приобретается практикой. Не зря говорят, что математике нельзя научиться, глядя, как это делает сосед. Самостоятельная работа и помощь учителя – вот залог плодотворной учебы.

1.Нестандартные задачи и их характеристики.

 

Наблюдения показывают, что математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решать задачи, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.

Нестандартные задачи способствуют развитию логического мышления в еще большей степени. Кроме того, они являются мощным средством активизациипознавательной деятельности, т. е. вызывают у детей огромный интерес и желание работать. Приведем пример нестандартных задач.

I. Задачи на смекалку.

1. Масса цапли, стоящей на одной ноге 12 кг. Сколько будет весить цапля, если встанет на 2 ноги?

2. Пара лошадей пробежала 40 км. Сколько пробежала каждая лошадь?

3. У семи братьев по одной сестре. Сколько всего детей в семье?

4. Шесть котов за шесть минут съедают шесть мышей. Сколько понадобится котов, чтобы за сто минут съесть сто мышей?

5. Стоят 6 стаканов, 3 с водой, 3 пустых. Как расставить их, чтобы стаканы с водой и пустые чередовались? Разрешается переставить только один стакан.

Рис. 1.

 

 

6. Геологи нашли 7 камней. Масса каждого камня: 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг и 7 кг. Эти камни разложили в 4 рюкзака так,

что в каждом рюкзаке масса камней оказалась одинаковой.

Как это сделали?

7. В классе причесанных девочек столько же, сколько непричесанных мальчиков. Кого в классе больше, девочек или непричесанных учеников?

8. Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток?

9. Миша говорит: «Позавчера мне было10 лет, а в следующем году мне исполнится 13 лет». Возможно ли это?

10. У Андрея и Бори 11 конфет, у Бори и Вовы 13 конфет, а у Андрея и Вовы – 12. Сколько всего конфет у мальчиков?

11.Отец с двумя сыновьями катались на велосипедах: двухколесных и трехколесных. Всего у них было 7 колес. Сколько было велосипедов, и каких?

12. Во дворе куры и поросята. У них у всех 5 голов и 14 ног. Сколько кур и сколько поросят?

13. По двору гуляют куры и кролики. Всего у них 12 ног. Сколько кур и сколько кроликов?

14.У каждого марсианина по 3 руки. Могут ли 13 марсиан взяться за руки так, чтобы не оставалось свободных рук?

15. Играя, каждая из трех девочек – Катя, Галя, Оля – спрятали одну из игрушек – медведя, зайца и слона. Катя не прятала зайца, Оля не прятала ни зайца, ни медведя. Кто какую игрушку спрятал?

II. Занимательные задачи.

1. Как расставить 6 стульев у 4 стен, чтобы у каждой стены было по 2 стула.

2. Папа с двумя сыновьями отправился в поход. На их пути встретилась река. У берега плот. Он выдерживает на воде одного папу или двух сыновей. Как переправиться на другой берег папе с сыновьями?

3. Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?

4. Четыре утенка и пять гусят весят 4кг100г, а пять утят и четыре гусенка весят 4кг. Сколько весят один утенок?

5. У мальчика было 22 монеты – пятирублевые и десятирублевые, всего на сумму 150 рублей. Сколько было пятирублевых и десятирублевых монет?

6. В квартире № 1, 2, 3 живут три котенка: белый, черный и рыжий. В квартире № 1 и 2 жил не черный котенок. Белый котенок жил не в квартире № 1. В какой квартире жил каждый из котят?

7.За пять недель пират Ерема способен выпить бочку рома. А у пирата Емели ушло б на это две недели. За сколько дней прикончат ром пираты, действуя вдвоем?

8.Лошадь съедает воз сена за месяц, коза - за два месяца, овца – за три месяца. За какое время лошадь, коза, овца вместе съедят такой же воз сена?

9.Двое очистили 400 картофелин; один очищал 3 штуки в минуту, другой -2. Второй работал на 25 минут больше, чем первый. Сколько времени работал каждый?

10. Среди футбольных мячей красный мяч тяжелее коричневого, а коричневый тяжелее зеленого. Какой мяч тяжелее: зеленый или красный?

11.Три кренделя, пять коврижек и шесть баранок стоят вместе 24 рубля. Что дороже: крендель или баранка?

12. Как тремя взвешиваниями на чашечных весах без гирь найти одну фальшивую (более легкую) монету из 20 монет?

13.Из верхнего угла комнаты вниз по стене поползли две мухи. Спустившись до полу, они поползли обратно. Первая муха ползла в оба конца с одинаковой скоростью, а вторая, хоть и поднималась вдвое медленнее первой, но зато спускалась вдвое быстрее ее. Какая из мух раньше приползет обратно?

14.В клетке находятся фазаны и кролики. У всех животных 35 голов и 94 ноги. Сколько в клетке кроликов и сколько фазанов?

15. Говорят, что на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «Половина моих учеников изучает математику, четвертая часть изучает природу, седьмая часть проводит время в молчаливом размышлении, остальная часть составляют 3 девы» Сколько учеников было у Пифагора?

 

III. Геометрические задачи.

1. Раздели пирог прямоугольной формы двумя разрезами на части так, чтобы они имели треугольную форму. Сколько получилось частей?

 

2. Нарисуй фигуру, не отрывая кончика карандаша от бумаги и не проводя дважды один и тот же отрезок.

 

3.Разрежь квадрат на 4 части и сложи из них 2 квадрата. Как это сделать?

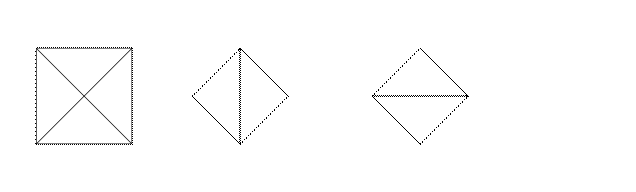
4.Убери 4 палочки так, чтобы осталось 5 квадратов.

 

 

5.Разрежьте треугольник на два треугольника, четырехугольник и пятиугольник, проведя две прямые линии.

6.Можно ли квадрат разделить на 5 частей и собрать восьмиугольник?

 

IV. Логические квадраты.

1. Заполни квадрат (4 _х 4) числами 1, 2, 3, 6 так, чтобы сумма чисел по всем строкам, столбцами и диагоналям была одинаковой. Числа в строках, столбцах и диагоналях не должны повторяться.

2. Раскрась квадрат красным, зеленым, желтым и синим цветами так, чтобы цвета в строках, столбцах и по диагоналям не повторялись.

 

красный			желтый
	зеленый
			синий

 

 

3.В квадрате нужно разместить еще числа 2,2,2,3,3,3 так, чтобы по всем линиям получить в сумме число 6.

 

 

4.Числа 3,4,5,6,8,9 расставить в клетках квадрата так, чтобы в любом направлении в сумме получить 21.

 

 

 

5.В клетках квадрата поставить числа 4,6,7,9,10,11,12 так, чтобы в столбцах, в строчках и по диагоналям получить сумму 24.

 

V. Комбинаторные задачи.

1. У Даши 2 юбки: красная и синяя, и 2 блузки: в полоску и в горошек. Сколько разных нарядов у Даши?

2. Сколько существует двузначных чисел, у которых все цифры нечетные?

3. Родители приобрели путевку в Грецию. До Греции можно добраться, используя один из трех видов транспорта: самолет, теплоход или автобус. Составьте все возможные варианты использования данных видов транспорта.

4. Сколько разных слов можно образовать при помощи букв слова «соединение»?

5. Из цифр 1, 3, 5 составить различные трехзначные числа так, чтобы в числе не было одинаковых цифр.

6. Встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас блондин, другой брюнет, а третий рыжеволосый. Но ни у одного нет волос того цвета, на который указывает его фамилия», - заметил брюнет. «Ты прав», - сказал Белов. Какой цвет волос у художника?

7. Три подруги вышли погулять в белом, зеленом и синем платьях и туфлях таких же цветов. Известно, что только у Ани цвет платья и цвет туфель совпадают. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель на каждой из подруг.

8. В отделении банка работают кассир, контролер и заведующий. Их фамилии Борисов, Иванов и Сидоров. Кассир не имеет ни братьев, ни сестер и меньше всех ростом. Сидоров женат на сестре Борисова и ростом выше контролера. Назовите фамилии контролера и заведующего.

9. Для пикника сладкоежка Маша взяла в трех одинаковых коробках конфеты, печенье и торт. На коробках были этикетки: «Конфеты», «Печенье», и «Торт». Но Маша знала, что мама любит шутить и всегда кладет продукты в

 

коробки, надписи на которых не соответствуют их содержимому. Маша была уверена, что конфеты не лежат в коробке, на которой написано «Торт». В какой же коробке торт?

10. По кругу сидят Иванов, Петров, Марков, Карпов. Их имена Андрей, Сергей, Тимофей, Алексей. Известно, Иванов не Андрей и не Алексей. Сергей сидит между Марковым и Тимофеем. Петров сидит между Карповым и Андреем. Как зовут Иванова, Петрова, Маркова и Карпова?

VI. Задачи на переливание.

1. Можно ли, имея лишь два сосуда емкостью 3 и 5л, набрать из водопроводного крана 4 л воды?

2. Как разделить поровну между двумя семьями 12 л хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: восьмилитровым и трехлитровым?

3.Как, имея два сосуда емкостью 9л и 5л, набрать из водоема ровно 3 литра воды?

4.Бидон, емкость которого 10 литров, наполнен соком. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить сок в два сосуда по 5 литров каждый?

5. Имеются два сосуда. Емкость одного из них 9л, а другого 4л. Как с помощью этих сосудов набрать из бака 6 литров некоторой жидкости? (Жидкость можно сливать обратно в бак).

 

Анализ предложенных текстовых задач показывает, что решение их не укладывается в рамки той или иной системы типовых задач. Такие задачи называют нетиповыми (И. К. Андронов, А. С. Пчелко и др.) или нестандартными (Ю. М. Колягин, К. И. Нешков, Д. Пойа и др.)

Обобщая различные подходы методистов в понимании стандартных и нестандартных задач (Д. Пойа, Я. М. Фридман и др.), под нестандартной задачей понимаем такую задачу, алгоритм которой не знаком учащемуся и в дальнейшем не формируется как программное требование.

Анализ учебников и учебных пособий по математике показывает, что каждая текстовая задача в определенных условиях может быть нестандартной, а в других – обычной, стандартной. Стандартная задача одного курса математики может быть нестандартной в другом курсе.

 

Например. «На аэродроме было 57 самолетов и 79 вертолетов, 60 машин поднялось в воздух. Можно ли утверждать, что в воздухе находится: а) хотя бы 1 самолет; б) хотя бы 1 вертолет?»

Такие задачи были необязательными для всех учащихся, они предназначались для наиболее способных к математике.

«Если хотите научиться решать задачи, то решайте их!» - советует Д. Пойа.

Главное при этом – сформировать такой общий подход к решению задач, когда задача рассматривается как объект для исследования, а ее решение – как конструирование и изобретение способа решения.

Естественно, что такой подход требует не бездумного решения огромного числа задач, а неторопливого, внимательного и обстоятельного решения значительно меньшего числа задач, но с последующим анализом проведенного решения.

Итак, общих правил решения нестандартных задач нет (поэтому – то эти задачи и называются нестандартными). Однако выдающиеся математики и педагоги (С.А. Яновская, Л.М. Фридман,

Э.Н. Балаян) нашли ряд общих указаний и рекомендаций, которыми можно руководствоваться при решении нестандартных задач. Эти указания обычно называют эвристическими правилами или, просто, эвристиками. Слово «эвристика» греческого происхождения и означает «искусство нахождения истины».

В отличие от математических правил эвристики носят характер необязательных рекомендаций, советов, следование которым может привести (а может и не привести) к решению задачи.

Процесс решения любой нестандартной задачи (по мнению

С.А. Яновской) состоит в последовательном применении двух операций:

1.сведение путем преобразований нестандартной задачи к другой, ей сходной, но уже стандартной задаче;

2. разбиение нестандартной задачи на несколько стандартных подзадач.

Для сведения нестандартной задачи к стандартной не существует определенных правил. Однако если внимательно, вдумчиво анализировать, решать каждую задачу, фиксируя в своей памяти все приемы, с помощью которых были найдены решения, какими методами были решены задачи, то вырабатывается умение в таком сведении.

 

Рассмотрим на примере задачи:

По тропинке, вдоль кустов, шел десяточек хвостов,

Сосчитать я также смог, что шагало тридцать ног.

Это вместе шли куда – то петухи и поросята.

Ну а мой вопрос таков – сколько было петухов?

И узнать я был бы рад - сколько было поросят?

Если не удается решить данную задачу, попытаемся свести ее к сходной.

Переформулируем:

1.Придумаем и решим похожую, но более простую.

2. Используем её решение для решения данной.

Трудность в том, что в задаче два типа зверей. Пусть все будут поросятами, тогда ног будет 40.

Составим похожую задачу:

По тропинке, вдоль кустов, шел десяточек хвостов.

Сосчитать я также смог, что шагало сорок ног.

Это вместе шли куда – то петухи и поросята.

Ну а мой вопрос таков - сколько было петухов?

И узнать я был бы рад – сколько было поросят?

Ясно, что если ног в 4 раза больше, чем хвостов, то все животные – поросята.

В похожей задаче взяли 40 ног, а в основной их было 30. Как уменьшить число ног? Заменить поросенка петушком.

Решение основной задачи: если бы все животные были поросятами, то у них было 40 ног. Когда заменяем поросенка петушком, число ног уменьшается на два. Всего надо сделать пять замен, чтобы получить 30 ног. Значит, шагало 5 петушков и 5 поросят.

Как придумать «похожую» задачу?

2 способ решения задачи.

В данной задаче можно применить принцип уравнивания.

Пусть все поросята встанут на задние ноги.

10*2 =20 столько ног шагает по тропинке

30 – 20 =10 столько передних ног у поросят

10:2 = 5 поросенка шло по тропинке

Ну а петушков 10 -5 =5.

Сформулируем несколько правил решения нестандартных задач.

1. «Простое» правило: не пропустите самую простую задачу.

Обычно простую задачу не замечают. А начинать надо именно с неё.

 

2. «Очередное» правило: условия по возможности надо менять по очереди. Количество условий - конечное число, так что до всех рано или поздно дойдет очередь.

3. «Неизвестное» правило: изменив одно условие, другое, связанное с ним обозначьте х, а потом подберите его так, чтобы вспомогательная задача решалась при данном значении и не решалась при увеличении х на единицу.

3. «Интересное » правило: делайте условия задачи более интересными.

4. «Временное» правило: если в задаче идет какой-то процесс и конечное состояние более определенно, чем начальное, стоит запустить время в обратную сторону: рассмотреть последний шаг процесса, потом предпоследний и т.д.

Рассмотрим применение этих правил.

Задача№1. Пять мальчиков нашли девять грибов. Докажите, что хотя бы двое из них нашли грибов поровну.

1шаг. Мальчиков очень много. Пусть их будет на 2 меньше в следующей задаче.

«Трое мальчиков нашли х грибов. Докажите, что хотя бы двое из них нашли грибов поровну».

Для доказательства установим, при каких х задача имеет решение.

При х=0, х=1, х=2 задача имеет решение, при х=3 задача не имеет решение.

Сформулируем похожую задачу.

Трое мальчиков нашли 2 гриба. Докажите, что хотя бы двое из них нашли грибов поровну.

Пусть все трое мальчиков нашли разное число грибов. Тогда минимальное число грибов равно 3, поскольку 3=0+1+2. Но по условию число грибов меньше 3, поэтому два мальчика из трех нашли одинаковое число грибов.

При решении исходной задачи рассуждения точно такие же. Пусть все, пять мальчиков, нашли разное число грибов. Минимальное число грибов тогда должно равняться 10. (10 =0+1+2+3+4). Но по условию число грибов меньше 10, поэтому двое мальчиков нашли одинаковое число грибов.

При решении использовали «неизвестное» правило.

Задача№2. Над озерами летели лебеди. На каждом садилась половина лебедей и еще пол-лебедя, остальные летели дальше. Все сели на семи озерах. Сколько было лебедей?

 

1шаг. Идет процесс, начальное состояние не определено, конечное – нулевое, т.е. не стало летящих лебедей.

Запускаем время в обратную сторону, придумав такую задачу:

Над озерами летели лебеди. На каждом взлетало пол-лебедя и еще столько, сколько теперь летело. Все взлетали с семи озер. Сколько было лебедей?

2шаг. Начинаем с нуля:

(((((((0+1/2)2+1/2)2+1/2)2+1/2)2+1/2)2+1/2)2+1/2)2 =127.

Задача №3.

У моста через речку встретились лодырь и черт. Лодырь пожаловался на свою бедность. В ответ черт предложил:

- Я могу помочь тебе. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки. Три раза переходил мост лодырь, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?

(((0+24):2+24):2+24):2= 21

При решении задач № 2и № 3 использовали «временное» правило.

Задача №4. Кузнец подковывает одно копыто за 15 минут. Сколько времени потребуется 8 кузнецам, чтобы подковать 10 лошадей. (Лошадь не умеет стоять на двух ногах).

1шаг. Лошадей и кузнецов слишком много, уменьшим пропорционально их количество, составив задачу.

Кузнец подковывает одно копыто за пять минут. Сколько времени потребуется четверым кузнецам, чтобы подковать пять лошадей?

Ясно, что минимально возможное время 25 минут, но может ли оно быть достигнуто? Необходимо организовать работу кузнецов без простоев. Будем действовать, не нарушая симметрии. Расположим пять лошадей по кругу. После того как четверо кузнецов подкуют каждый одно копыто лошади, кузнецы сдвинутся на одну лошадь по кругу. Чтобы обойти полный круг, потребуется пять тактов работы по пять минут. Во время 4 тактов каждая лошадь будет подковываться, а один такт отдыхать. В итоге все лошади будут подкованы за 25 минут.

2 шаг. Возвращаясь к исходной задаче, заметим, что 8=2* 4, а 10=2*5. Тогда 8 кузнецов нужно разбить на две бригады

 

 

по 4 человека в каждой, а лошадей – на два табуна по 5 лошадей в каждом.

За 25 минут первая бригада кузнецов подкует первый табун, а вторая – второй.

При решении использовалось «очередное» правило.

Конечно, может встретиться задача, к которой не удастся применить ни одного из перечисленных правил. Тогда нужно изобрести особый метод решения этой задачи.

Необходимо помнить, что решение нестандартных задач есть искусство, которым можно овладеть лишь в результате постоянного самоанализа действий по решению задач.

 

 

2. Образовательные функции нестандартных задач.

 

Роль нестандартных задач в формировании логического мышления.

На современном этапе обучения наметилась тенденция использования задач как необходимого компонента обучения учащихся математике. Объясняется это, прежде всего, возрастающими требованиями, направленными на усиление развивающих функций обучений.

Понятие «нестандартная задача» используется многими методистами. Так, Ю. М. Колягин раскрывает это понятие следующим образом: «Под нестандартной понимается задача, при предъявлении которой учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение».

Опираясь на анализ теории и практики использования нестандартных задач в обучении математике, установлена их общая и специфическая роль.

 

Нестандартные задачи:

- учат детей использовать не только готовые алгоритмы, но и самостоятельно находить новые способы решения задач, т. е. способствуют умению находить оригинальные способы решения задач;

- оказывают влияние на развитие смекалки, сообразительности учащихся;

препятствуют выработке вредных штампов при решении задач, разрушают неправильные ассоциации в знаниях и умениях учащихся, предполагают не столько усвоение алгоритмических приемов, сколько нахождение новых связей в знаниях, к переносу

 

знаний в новые условия, к овладению разнообразными приемами умственной деятельности;

 

- создают благоприятные условия для повышения прочности и глубины знаний учащихся, обеспечивают сознательное усвоение математических понятий.

 

Нестандартные задачи:

- не должны иметь уже готовых, заученных детьми алгоритмов;

- должны быть доступны по содержанию всем учащимся;

- должны быть интересными по содержанию;

- для решения нестандартных задач учащимся должно хватать знаний, усвоенных ими по программе.

 

 

3.Методика формирования умения решать нестандартные задачи.

Задача№1.

- По пустыне медленно идет караван верблюдов, всего их 40. Если пересчитать все горбы у этих верблюдов, то получится 57 горбов. Сколько в этом караване одногорбых верблюдов?

- Сколько горбов может быть у верблюдов?

(их может быть два или один)

Давайте каждому верблюду на один горб прикрепим цветок.

- Сколько цветков потребуется? (40 верблюдов – 40 цветов)

- Сколько верблюдов останется без цветов?

( Таких будет 57-40=17. Это вторые горбы двугорбых верблюдов ).

- Сколько двугорбых верблюдов? (17)

- Сколько одногорбых верблюдов? (40-17=23)

- Каков же ответ задачи? (17 и 23 верблюдов).

Задача № 2.

-В гараже стояли легковые машины и мотоциклы с колясками, всех вместе 18. У машин и мотоциклов – 65 колес. Сколько мотоциклов с колясками стояло в гараже, если у машин 4 колеса, а у мотоцикла – 3 колеса?

Переформулируем задачу. Грабители, пришедшие в гараж, где стояли 18 машин и мотоциклов с колясками, сняли с каждой машины и каждого мотоцикла по три колеса и унесли. Сколько колес осталось в гараже, если их было 65? Машине или мотоциклу они принадлежат?

- Сколько колес унесли грабители? (3*18=54колес)

- Сколько осталось колес? (65-54=11)

- Сколько машин было в гараже?

Или

-В гараже стояли 18 легковых машин и мотоциклов с коляской. У машин и мотоциклов 65 колес. Сколько в гараже мотоциклов, если в каждую коляску положили запасное колесо?

- Сколько стало колес у машин и мотоциклов вместе? (4*18=72)

- Сколько запасных колес положили в каждую коляску? (72-65= 7)

- Сколько машин в гараже? (18-7=1)

 

Задача №3.

-Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35 кг сена. Сколько сена выдают одной лошади и сколько одной корове?

Запишем краткое условие задачи:

1 лошади и 2 коров -34кг.

2 лошадей и 1 коров -35кг.

Можно ли узнать, сколько сена потребуется для 3 лошадей и 3 коров? (для 3 лошадей и 3 коров – 34+35=69 кг)

Можно ли узнать, сколько сена потребуется для одной лошади и одной коровы? (69 : 3 – 23кг)

Сколько сена потребуется для одной лошади? (35-23=12кг)

Сколько сена потребуется для одной коровы? (23 -13 =11кг)

Ответ: 12кг и 11 кг

Задача№4.

-Летели гуси: 2 впереди, 1 позади, 1 впереди, 2 позади.

Сколько гусей летело?

- Сколько летело гусей, как сказано в условии? (2 впереди, 1 позади)

- Изобразите это точками.

- Что сказано дальше? (1 впереди, 2 позади)

- Изобразите точками.

- Посчитайте то, что у вас получилось (2 впереди, 1, 1, 2 позади)

- Так говорится в условии? (нет)

- Значит, вы нарисовали гусей лишних. По вашему рисунку можно сказать, что 2 впереди и 4 позади, или 4 впереди, а 2 позади. А это не по условию. Что же нужно сделать? (убрать 3 последние точки)

- Что получится?

- Так сколько же гусей летело? (3)

Задачи № 5.

-Четыре утенка и пять гусят весят 4кг 100г, пять утят и четыре гусенка весят 4 кг. Сколько весит один утенок?

Переформулируем задачу.

Четыре утенка и пять гусят весят 4кг 100г, пять утят и четыре гусенка весят 4 кг.

-Сколько весят один утенок и один гусенок вместе?

- Сколько весят 9 утят и 9 гусят вместе?

Примените решение вспомогательной задачи для решения основной, зная сколько весят 3 утенка и 3 гусенка вместе?

 

Задачи с элементами комбинаторики и на смекалку.

Задача № 6.

-Марина решила позавтракать в школьном буфете. Изучи меню и ответь, сколькими способами она может выбрать напиток и кондитерское изделие?

 

Напитки	Кондитерские изделия
Чай	Ватрушка
Молоко	Печенье
Компот	Булочка

 

- Давайте предположим, что из напитков Марина выберет чай. Какое кондитерское изделие она может подобрать к чаю? (чай – ватрушка, чай – печенье, чай – булка)

- Сколько способов? (3)

- Как будем рассуждать дальше? (Если Марина выберет молоко, то тоже может выбрать к нему кондитерское изделие тремя способами)

- А если компот? (тоже 3)

- Как же узнать, сколько способов может Марина использовать, чтобы выбрать себе обед? (3+3+3=9)

- Да, вы правы. Но чтобы нам было легче решать такую задачу, мы будем использовать графы. Обозначим напитки и кондитерские изделия точками и соединим пары тех блюд, которые выберет Марина.

 

чай молоко компот

ватрушка печенье булочка

 

 

Теперь сосчитаем количество линий. Их 9. Значит, существует 9 способов выбора блюд.

Задача № 7.

-Три богатыря – Илья Муромец, Алеша Попович и Добрыня Никитич, защищая от нашествия родную землю, срубили Змею Горынычу все 13 голов. Больше всех голов срубил Илья Муромец, а меньше всех – Алеша Попович. Сколько голов мог срубить каждый из них?

- Кто может ответить на этот вопрос?

(учитель спрашивает несколько человек – ответы у всех разные)

- Почему получились разные ответы? (потому что не сказано конкретно, сколько голов срубил хотя бы один из богатырей)

- Давайте попробуем найти все возможные варианты решения этой задачи. Поможет нам в этом таблица.

 

Богатыри	Возможное число срубленных голов
Алеша Попович
Добрыня Никитич
Илья Муромец

 

- Какое условие мы обязательно должны соблюдать, решая эту задачу? (Все богатыри срубили разное количество голов, и у Алеши – меньше всех, у Ильи – больше всех)

- Сколько же вариантов решения имеет данная задача? (8)

Такие задачи называют – задачи с многовариантными решениями.

Составьте свою задачу с многовариантным решением.

 

Задача № 8.

-В битве с трехглавым и треххвостым Змеем Горынычем

Иван-Царевич одним ударом меча может срубить либо одну голову, либо две головы, либо один хвост, либо два хвоста. Если срубить одну голову – новая вырастет, если срубить один хвост – два новых вырастут, если срубить два хвоста – голова вырастет, если срубить две головы – ничего не вырастет. Посоветуйте Ивану-Царевичу, как поступить, чтобы он мог срубить Змею все головы и хвосты.

- Что же произойдет, если Иван-Царевич отрубит одну голову? (вырастет новая голова)

- Есть смысл отрубать одну голову? (нет, ничего не изменится)

- Значит, отрубание одной головы исключаем - лишняя трата сил и времени.

- Что произойдет, если отрубить один хвост? (вырастут два новых хвоста)

- А если отрубить два хвоста? (вырастет голова)

- А две головы? (ничего не вырастет)

- Итак, мы не можем срубить одну голову, т. к. при этом ничего не изменится, опять вырастет голова. Надо добиться такого положения, чтобы голов было четное число, а хвостов – ни одного. Но для этого нужно, чтобы и хвостов было четное число.

- Как же можно добиться нужного результата?

1). 1-ый удар: срубить 2 хвоста – станет 4 головы и 1 хвост;

2-ой удар: срубить 1 хвост – станет 4 головы и 2 хвоста;

3-ий удар: срубить 1 хвост – станет 4 головы и 3 хвоста;

4-ый удар: срубить 1 хвост – станет 4 головы и 4 хвоста;

5-ый удар: срубить 2 хвоста – станет 5 голов и 2 хвоста;

6-ой удар: срубить 2 хвоста – станет 6 голов и 0 хвостов;

7-ой удар: срубить 2 головы – станет 4 головы;

8-ой удар: срубить 2 головы – станет 2 головы;

9-ый удар: срубить 2 головы – станет 0 голов.

2). 1-ый удар: срубить 2 головы – станет 1 голова и 3 хвоста;

2-ой удар: срубить 1 хвост – станет 1 голова и 4 хвоста;

3-ий удар: срубить 1 хвост – станет 1 голова и 5 хвостов;

4-ый удар: срубить 1 хвост – станет 1 голова и 6 хвостов;

5-ый удар: срубить 2 хвоста – станет 2 головы и 4 хвоста;

6-ой удар: срубить 2 хвоста – станет 3 головы и 2 хвоста;

7-ой удар: срубить 2 хвоста – станет 4 головы;

8-ой удар: срубить 2 головы – станет 2 головы;

9-ый удар: срубить 2 головы – станет 0 голов.

Задача № 9.

-В семье четверо детей: Сережа, Ира, Витя и Галя. Им 5, 7, 9 и 11 лет. Сколько лет каждому из них, если один из мальчиков ходит в детский сад, Ира моложе Сережи, а сумма лет девочек делится на 3?

- Повторите условие задачи.

- Чтобы не запутаться в процессе рассуждений начертим таблицу.

Таблица

возраст имя	5 лет	7 лет	9 лет	11 лет
Сережа
Ира
Витя
Галя

 

- Что мы знаем про одного из мальчиков? (ходит в детский сад)

- Сколько лет этому мальчику? (5)

- Этого мальчика могут звать Сережа? (нет, Сережа старше Иры, значит, его зовут Витя)

Таблица

возраст имя	5 лет	7 лет	9 лет	11 лет
Сережа
Ира
Витя	+
Галя

 

Поставим в строке «Витя», столбце «5» знак «+». Значит, самого младшего ребенка зовут Витя и ему 5 лет.

- Что знаем про Иру? (она младше Сережи, и если к ее возрасту прибавить возраст другой сестры, то эта сумма будет делиться на 3)

- Попробуем вычислить все суммы чисел 7, 9 и 11.

7+9=16

9+11=20

7+11=18

16 и 20 на 3 не делится, а 18 на 3 делится.

- Значит, возраст девочек 7 и 11 лет.

- Сколько лет Сереже? (9)

- А Ире? (7, т. к. она младше Сережи)

- А Гале? (11 лет)

- Заносим данные в таблицу:

 

возраст имя	5 лет	7 лет	9 лет	11 лет
Сережа			+
Ира		+
Витя	+
Галя				+

- Какой же ответ на вопрос задачи? (Вите 5 лет, Ире 7 лет, Сереже 9 лет, а Гале 11 лет)

Задача №10.

-Катя, Соня, Галя и Тома родились 2 марта, 17 мая, 2 июня, 20 марта. Соня и Галя родились в одном месяце, а у Гали и Кати день рождения обозначился одинаковыми числами. Кто, какого числа, и в каком месяце родился?

- Прочитайте задачу.

- Что знаем? (что Соня и Галя родились в одном месяце, а Галя и Катя – в одно число)

- Значит, в каком месяце день рождения у Сони и Гали? (в марте)

- А что можно сказать про Галю, зная, что она родилась в марте, да еще ее число совпадает с числом Кати? (Галя родилась 2 марта)

- Когда же родилась Катя? (2 июня)

- А когда день рождения у Сони? (17 мая)

- А у Томы? (20 марта)

- Чтобы легче было решать эту задачу можно использовать такую таблицу:

 

Катя, Соня	2 марта, 17 мая	Соня один	Катя - ?	2 июня
Галя, Тома	2 июня, 20 марта	Галя месяц	Соня - ?	20 марта
		Галя одно	Галя - ?	2 марта
		Катя число	Тома - ?	17 мая

Зада