 |
Главная |
Элементы квантовой статистики
|
из
5.00
|
A C
x
O B 
Найдем 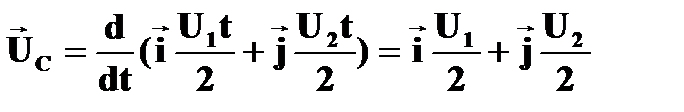
Тогда скорость частиц в СУМ:
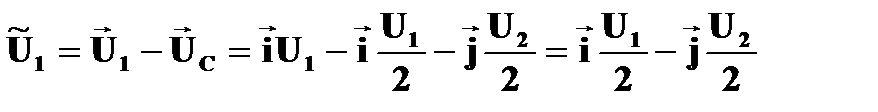
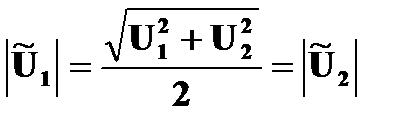 -очевидно
-очевидно
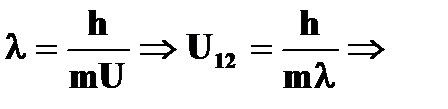
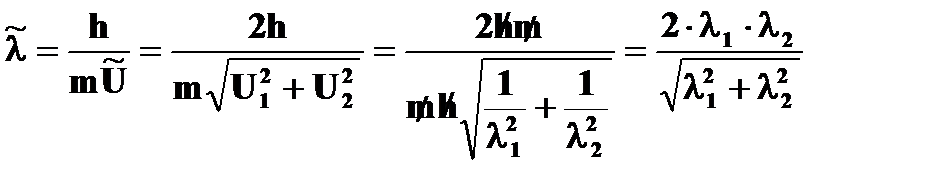
Ответ: 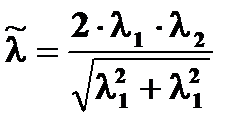 .
.
Задача 3.
Оценить минимальную кинетическую энергию электрона, локализованного в области размером 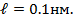
Ответ: 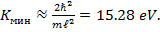 (при условии
(при условии 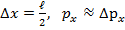 )
)
Используя соотношение неопределенности:
∆р*∆х=ħ
∆р= ħ/∆х
Eкин=∆р^2/2m= ħ^2/(2m∆х^2)
Если принимать : 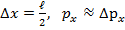
∆р= 2ħ/∆х
Eкин=∆р^2/2m= 4*ħ^2/(2m∆х^2)=2*ħ^2/(m∆х^2)
Задача 4.
Частица находится в одномерной потенциальной яме шириной 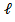 с бесконечно высокими “стенками”. Оценить силу давления частицы на стенки при минимально возможном значении её энергии Емин.
с бесконечно высокими “стенками”. Оценить силу давления частицы на стенки при минимально возможном значении её энергии Емин.
Ответ: 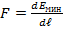 = 2Емин/
= 2Емин/ 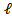 ,
, 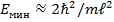 (при условии
(при условии 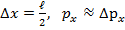 ).
).

По Условию Дунаевского из ответа:

Задача 5.
Оценить с помощью соотношения неопределенностей минимально возможную энергию в атоме водорода и соответствующее эффективное расстояние его от ядра.
Ответ: 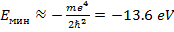 ,
, 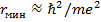 = 0.53
= 0.53 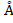 (при условии
(при условии 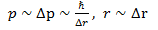 ).
).


Задача 6.
Оценить с помощью соотношения неопределенностей минимально возможную энергию в поле U(x) = a|x| (a>0).
Ответ: 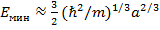
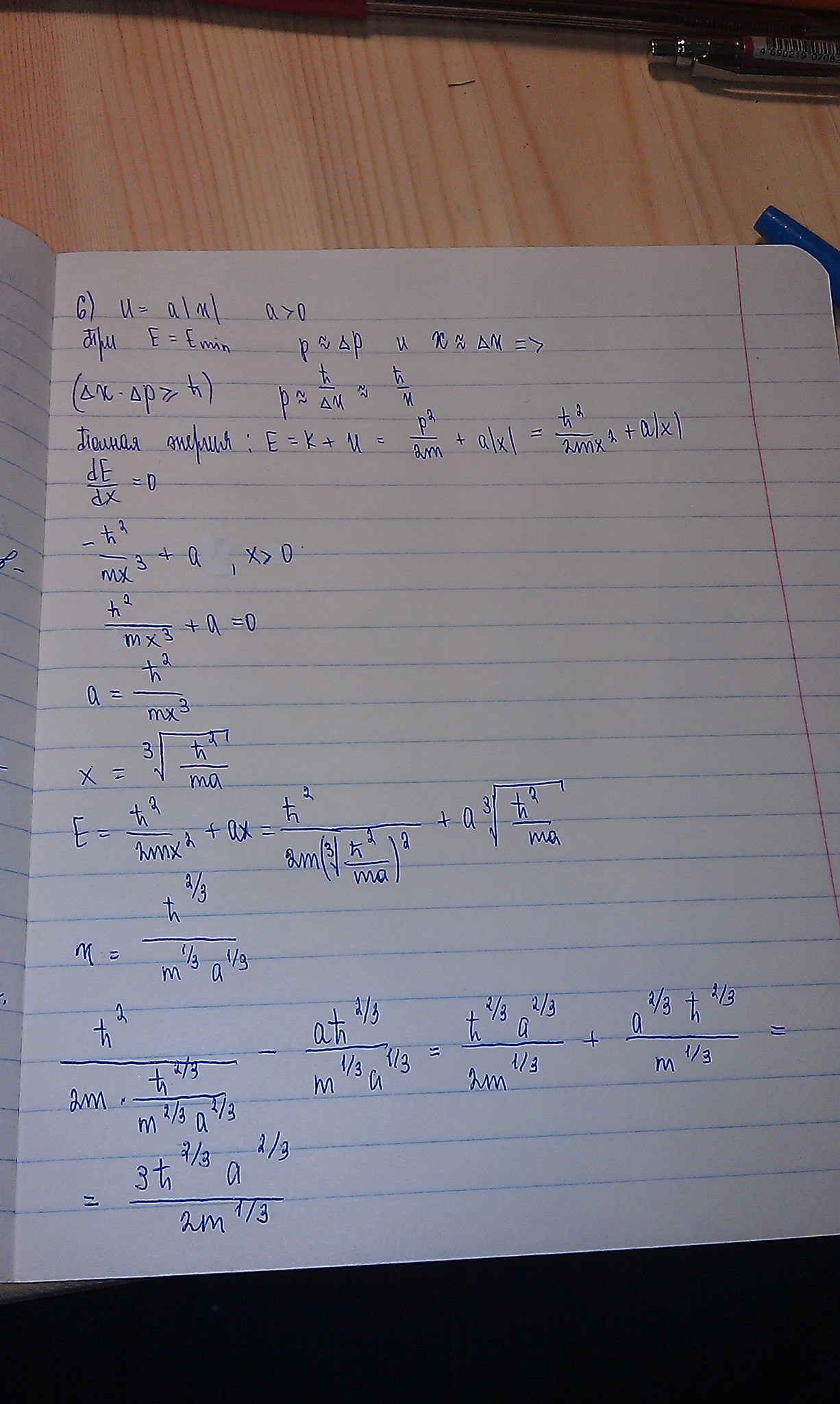
Задача7.
Найти собственное значение оператора 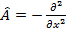 , принадлежащее волновой функции
, принадлежащее волновой функции 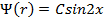 .
.
Ответ: A=4

Задача 8.
Найти наиболее вероятное расстояние электрона от ядра атома водорода в состоянии 2р.
Ответ: r0 = 4a0 ( 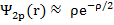 ,
, 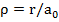 ,
, 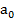 – первый боровский радиус)
– первый боровский радиус)
Задача9.
Определить энергию электрона атома водорода в стационарном состоянии:
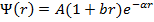 , где A, b и α – некоторые постоянные.
, где A, b и α – некоторые постоянные.
Решение.
Так как волновая функция зависит только от r, то уравнение Шредингера в сферической системе координат имеет вид
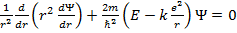 , (1.1)
, (1.1)
где 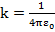 . Удобно представить волновую функцию в виде
. Удобно представить волновую функцию в виде
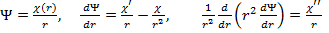 (1.2)
(1.2)
В результате получаем уравнение
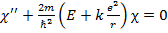 (1.3)
(1.3)
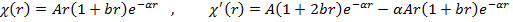
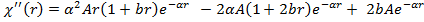
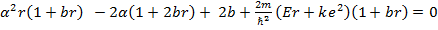 (1.4)
(1.4)
Приравнивая коэффициенты при степенях r, получаем:
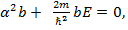 (1.5a)
(1.5a)
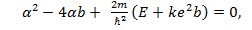 (1.5b)
(1.5b)
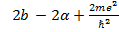 k = 0 (1.5c)
k = 0 (1.5c)
Из первого равенства следует, что
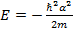 (1.6)
(1.6)
А) Если b=0, то из (1.5c) мы получаем энергию основного состояния
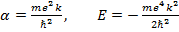 (= - 13.6 eV) (1.7)
(= - 13.6 eV) (1.7)
Б) Если b≠0, то
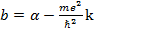 (1.8)
(1.8)
Значение 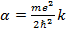 , отвечающее условию b≠0 находится из решения квадратного уравнения (1.5b). Постоянная
, отвечающее условию b≠0 находится из решения квадратного уравнения (1.5b). Постоянная 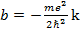 , а энергия (отвечающая значению n=2) в соответствии с (1.6) равна
, а энергия (отвечающая значению n=2) в соответствии с (1.6) равна
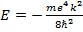 (1.9)
(1.9)
Задача 10.
Найти возможные значения энергии частицы массы m, находящейся в сферически-симметричной потенциальной яме (U(r)=0 при r < r0 и U(r) = ∞ при r > r0) для случая, когда волновая функция зависит только от r.
Ответ: 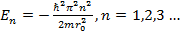 (Указание: воспользоваться подстановкой
(Указание: воспользоваться подстановкой 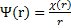 и учесть, что волновая функция должна оставаться конечной при
и учесть, что волновая функция должна оставаться конечной при 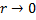 ).
).
1 решение: http://sanish1.narod.ru/kv_fiz/5.138.htm
2 решение:
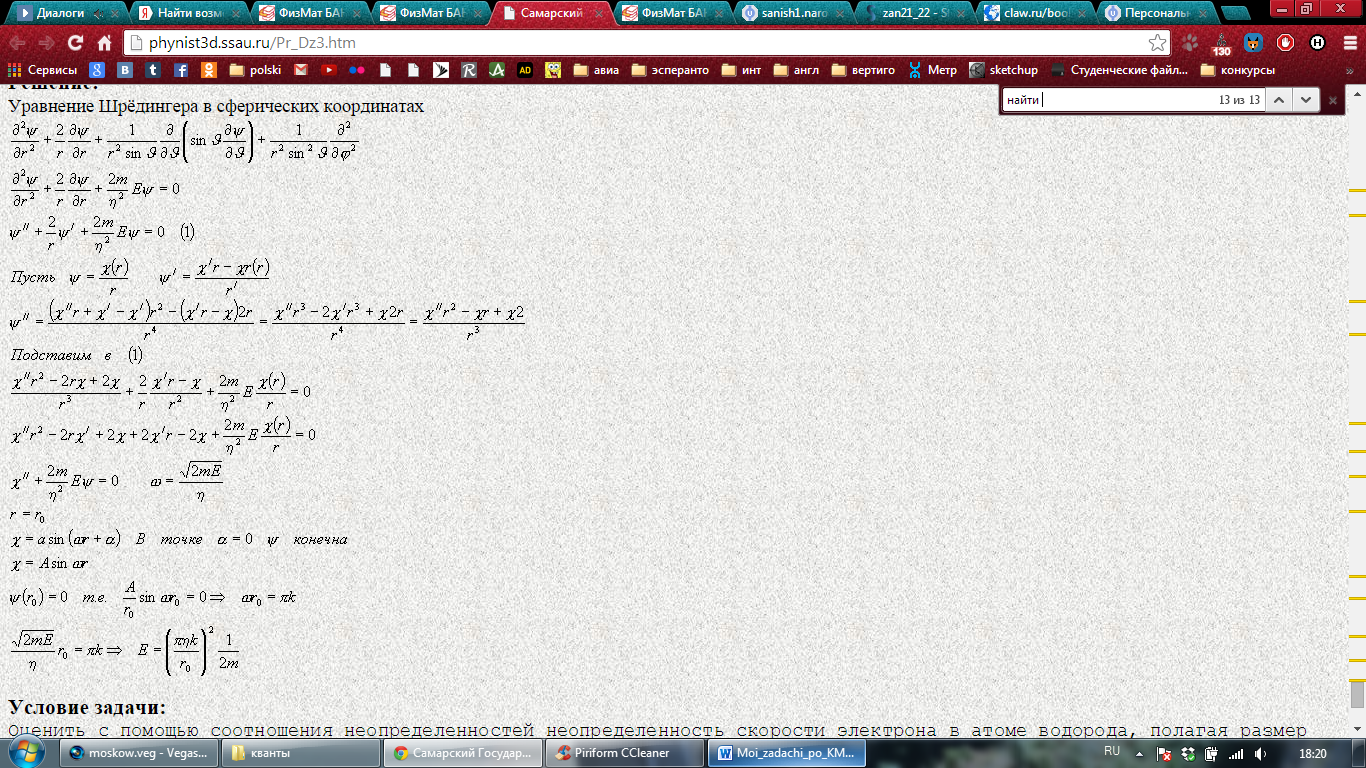
Задача 11.
Волновая функция частицы в сферически-симметричном центральном поле имеет вид 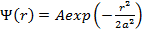 , где a - некоторая постоянная. Найти
, где a - некоторая постоянная. Найти 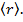
Ответ: 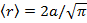
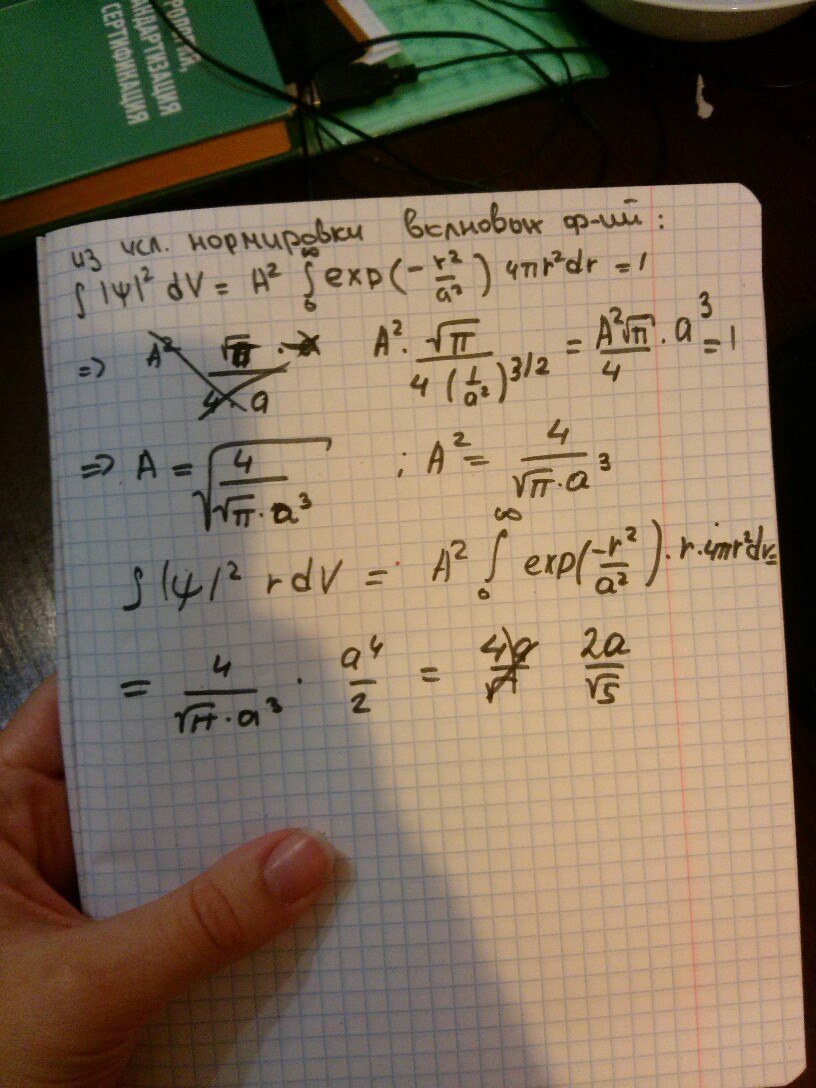
Задача 12.
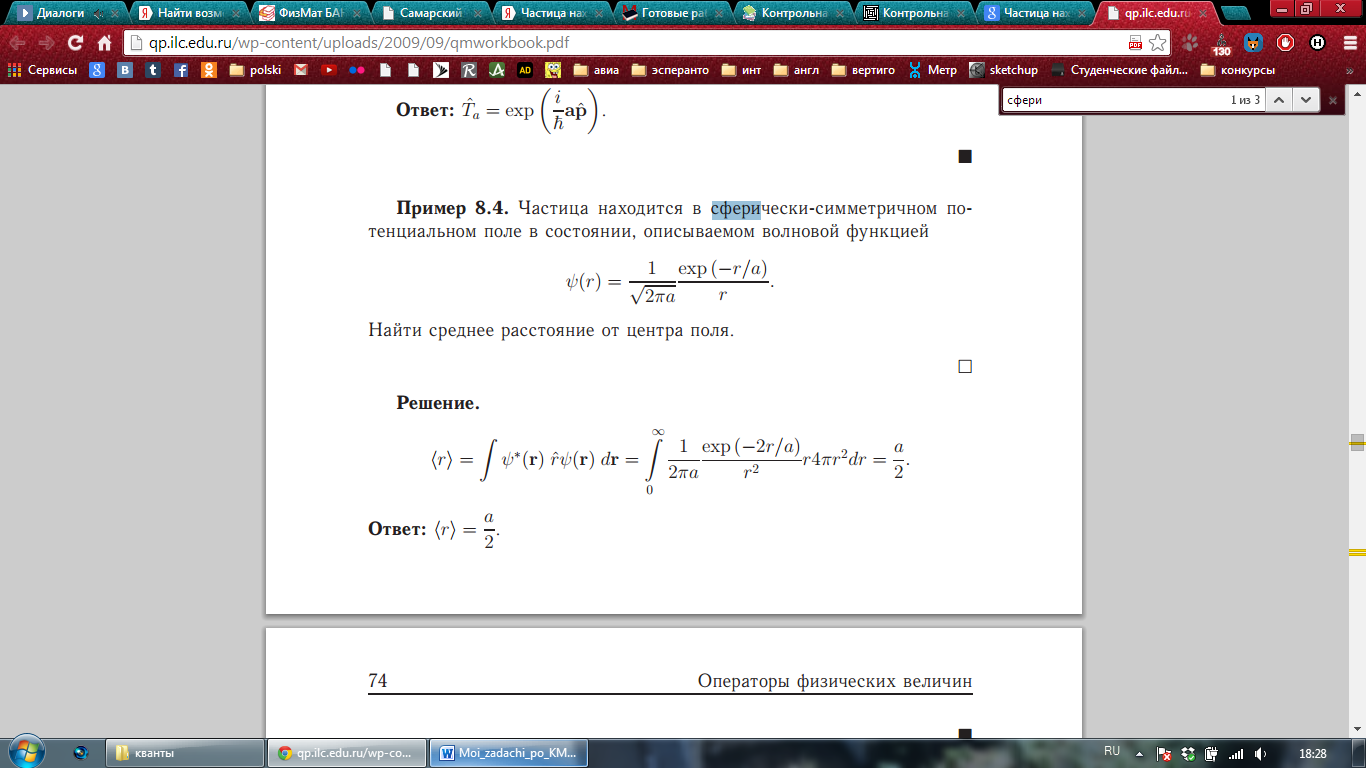
Частица находится в сферически-симметричном центральном поле в состоянии 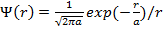 , где r – расстояние от центра, a- некоторая постоянная. Найти
, где r – расстояние от центра, a- некоторая постоянная. Найти 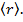
Ответ: 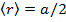
Решение:
Задача 13.
Частица в момент времениt=0 находится в состоянии 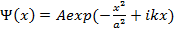 , где A и a- некоторые постоянные. Найти:
, где A и a- некоторые постоянные. Найти: 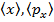 .
.
Ответ: 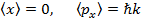 .
.
Решение:
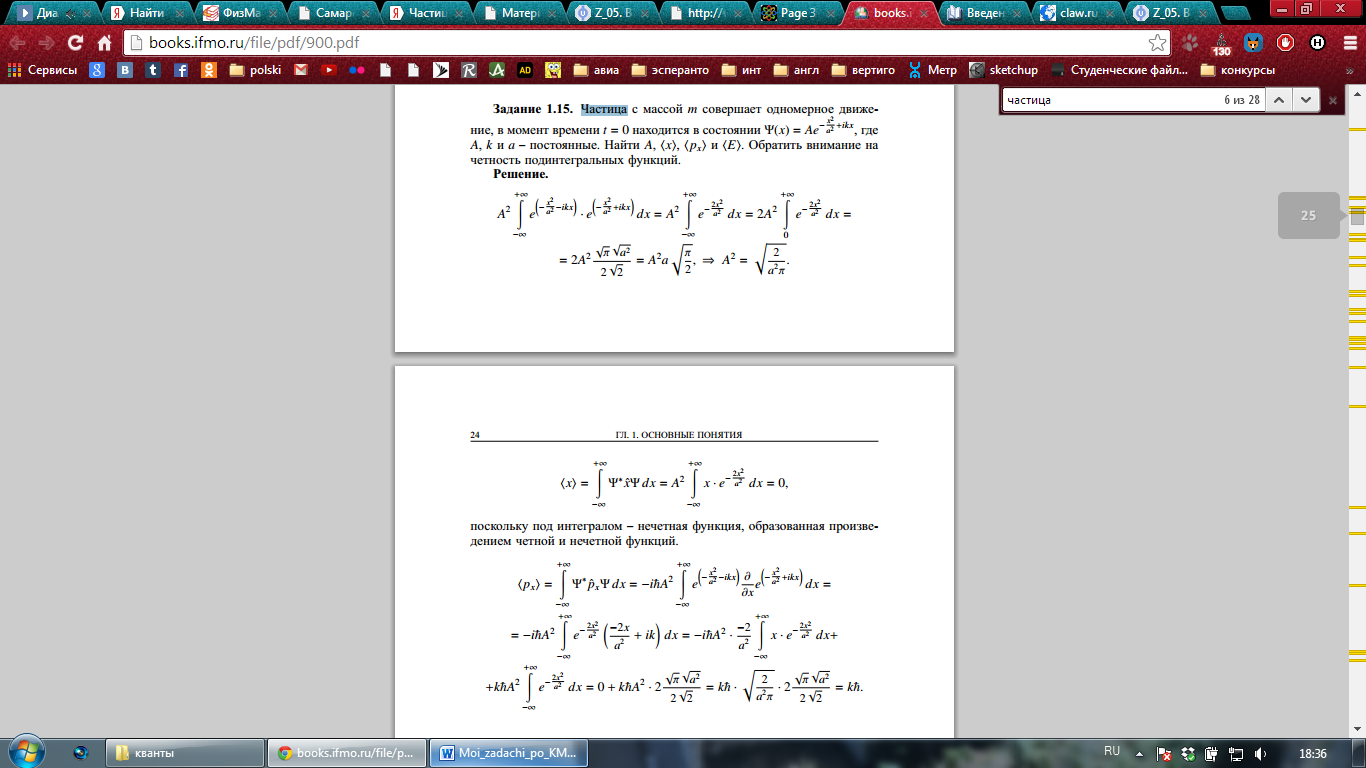
Задача 14.
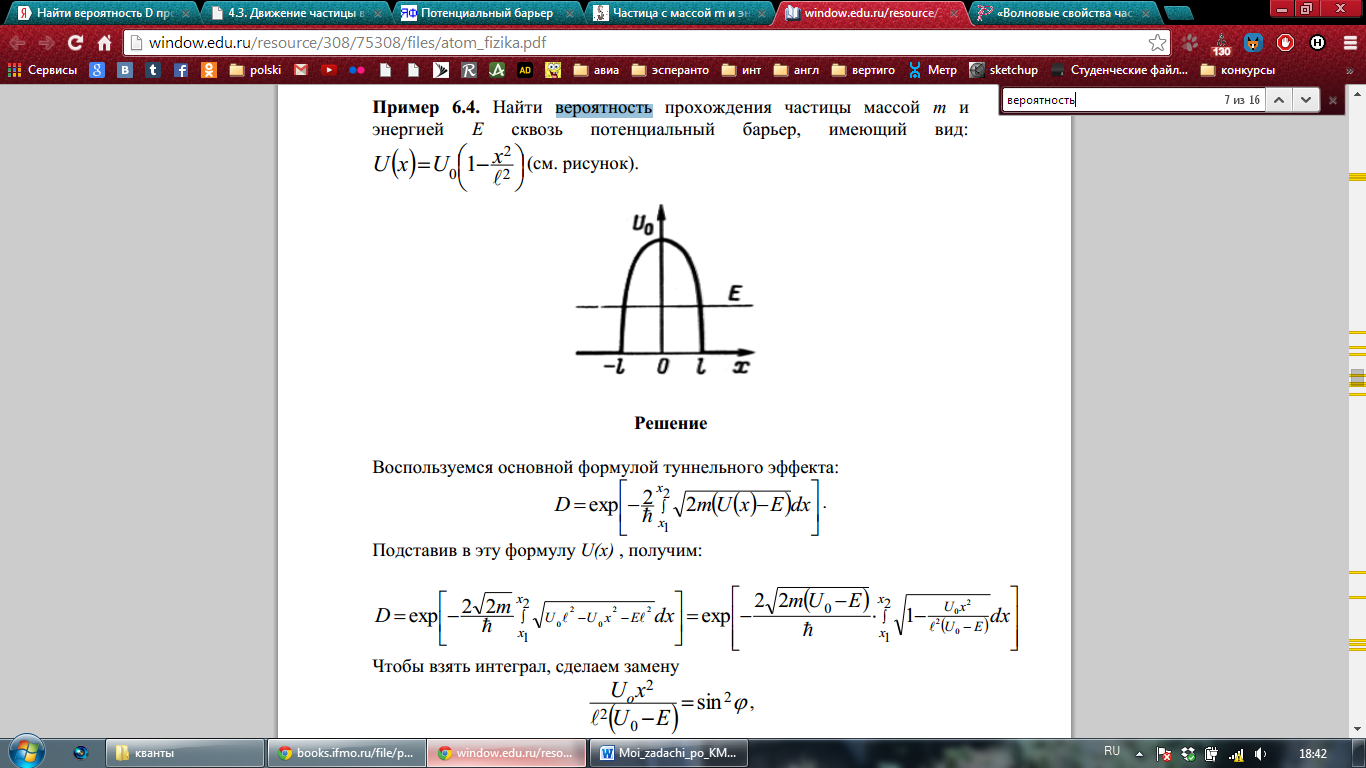
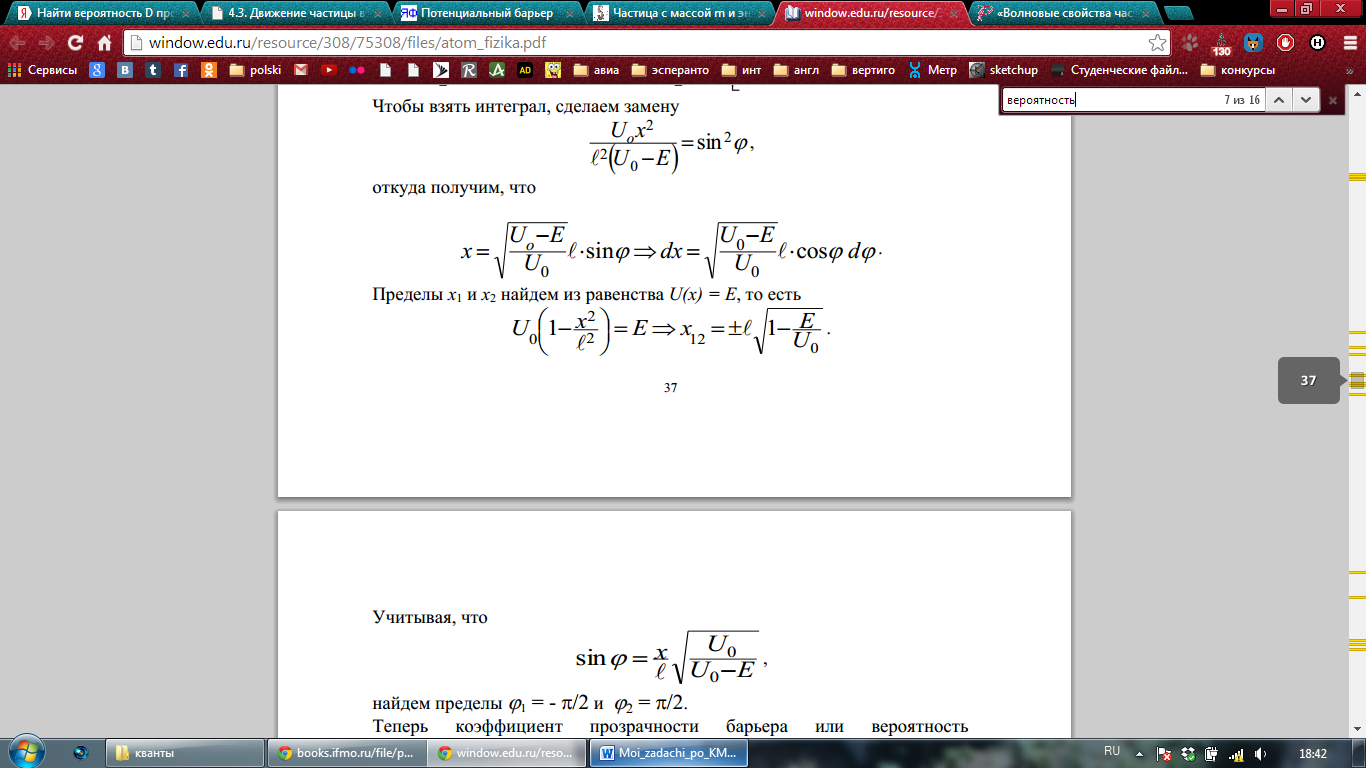
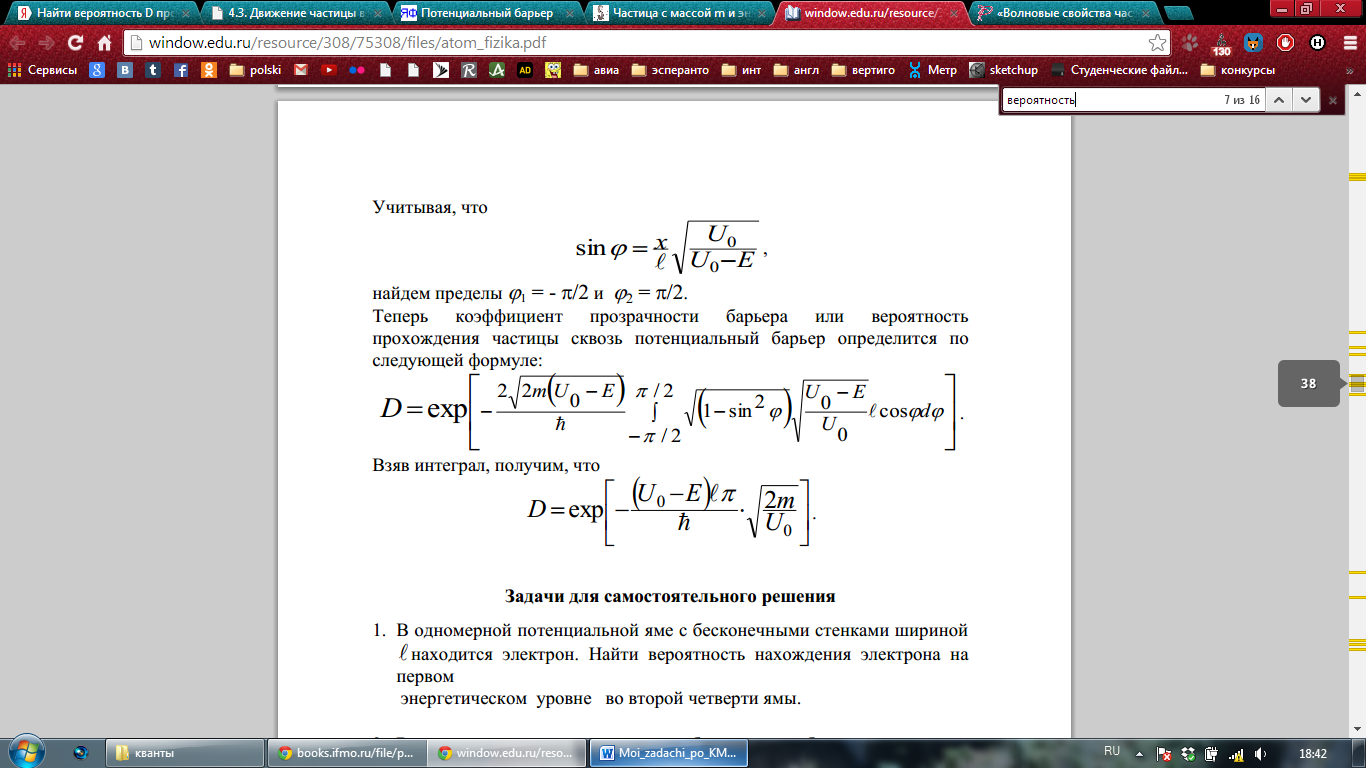
Найти вероятность D прохождения частицы с массой и энергией Е сквозь потенциальный барьер 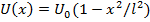 .
.
Ответ: 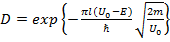
Решение:
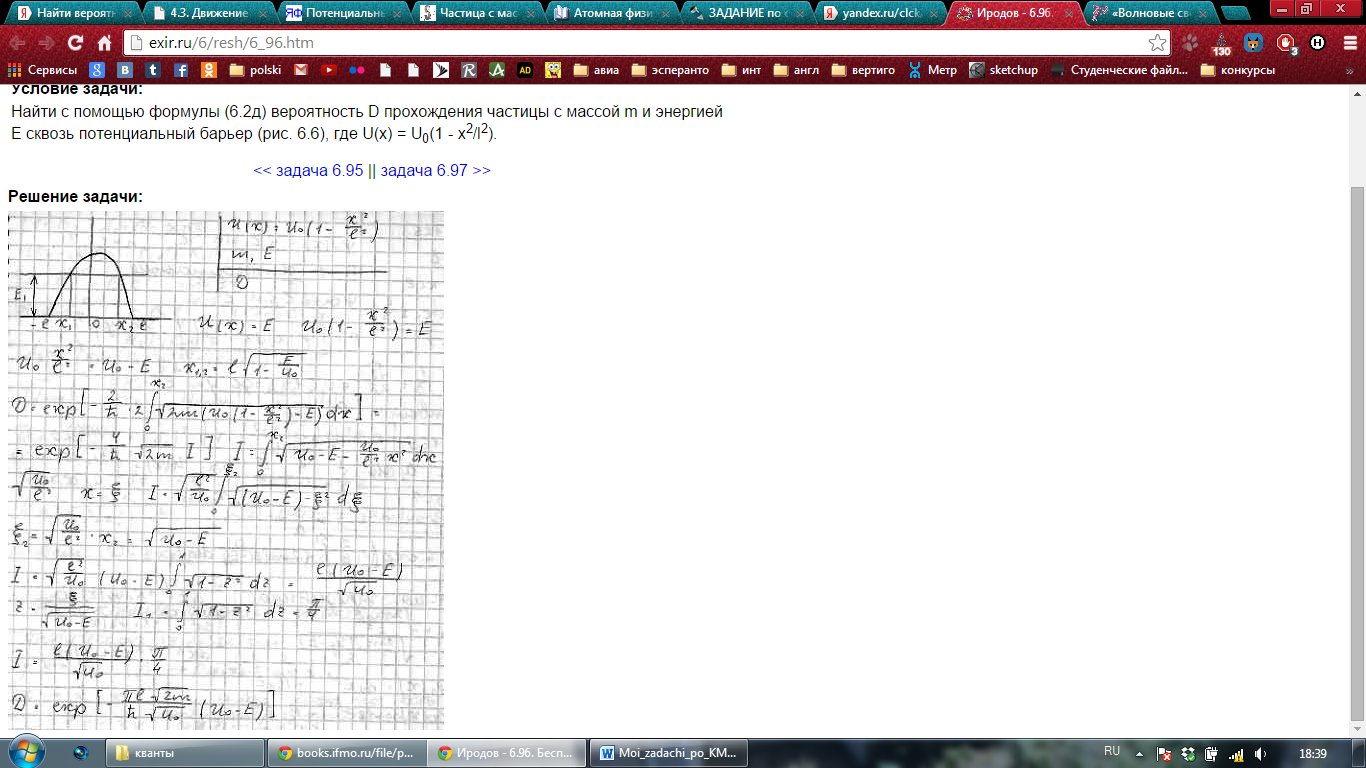
Решение 2:
Задача 15.
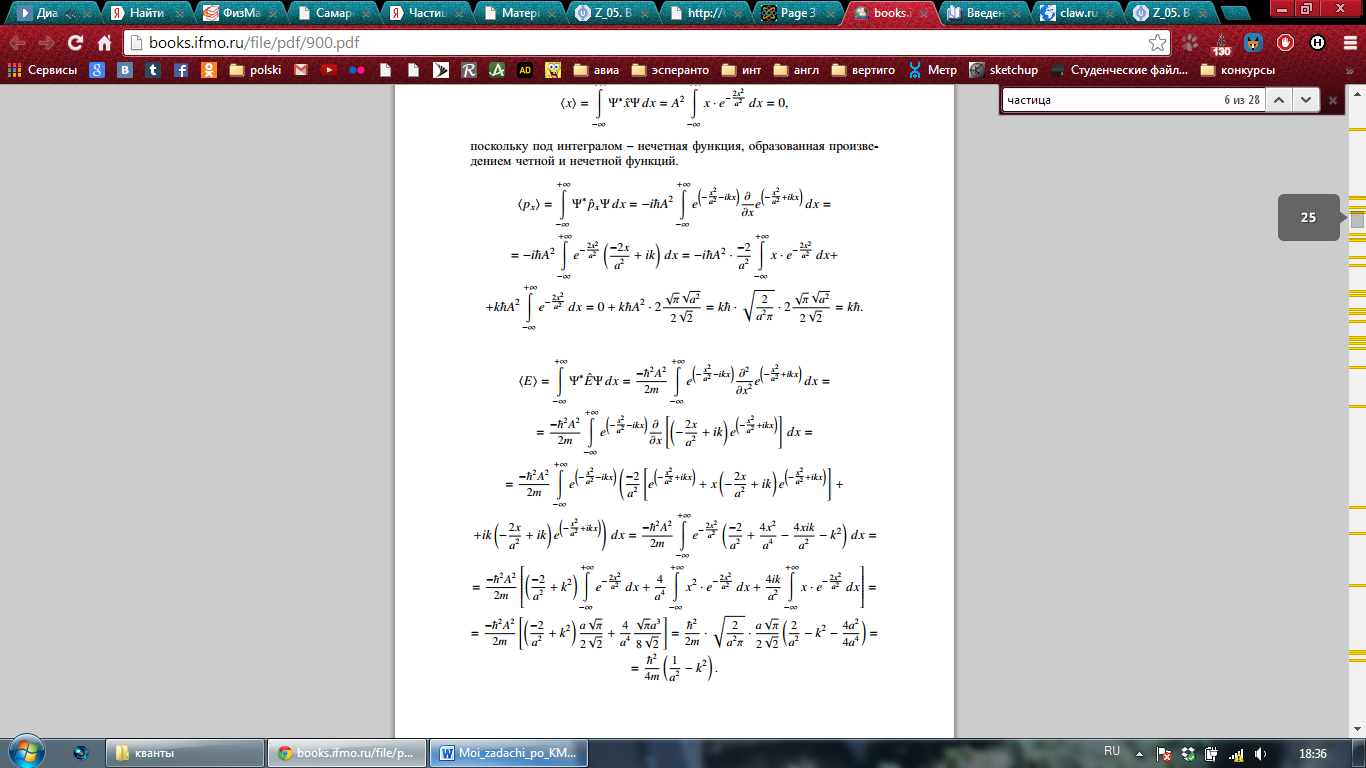
Определите среднее значение координаты электрона в одномерной яме шириной 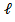 с бесконечно высокими “стенками”.
с бесконечно высокими “стенками”.
Ответ: 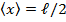
Может это решение:
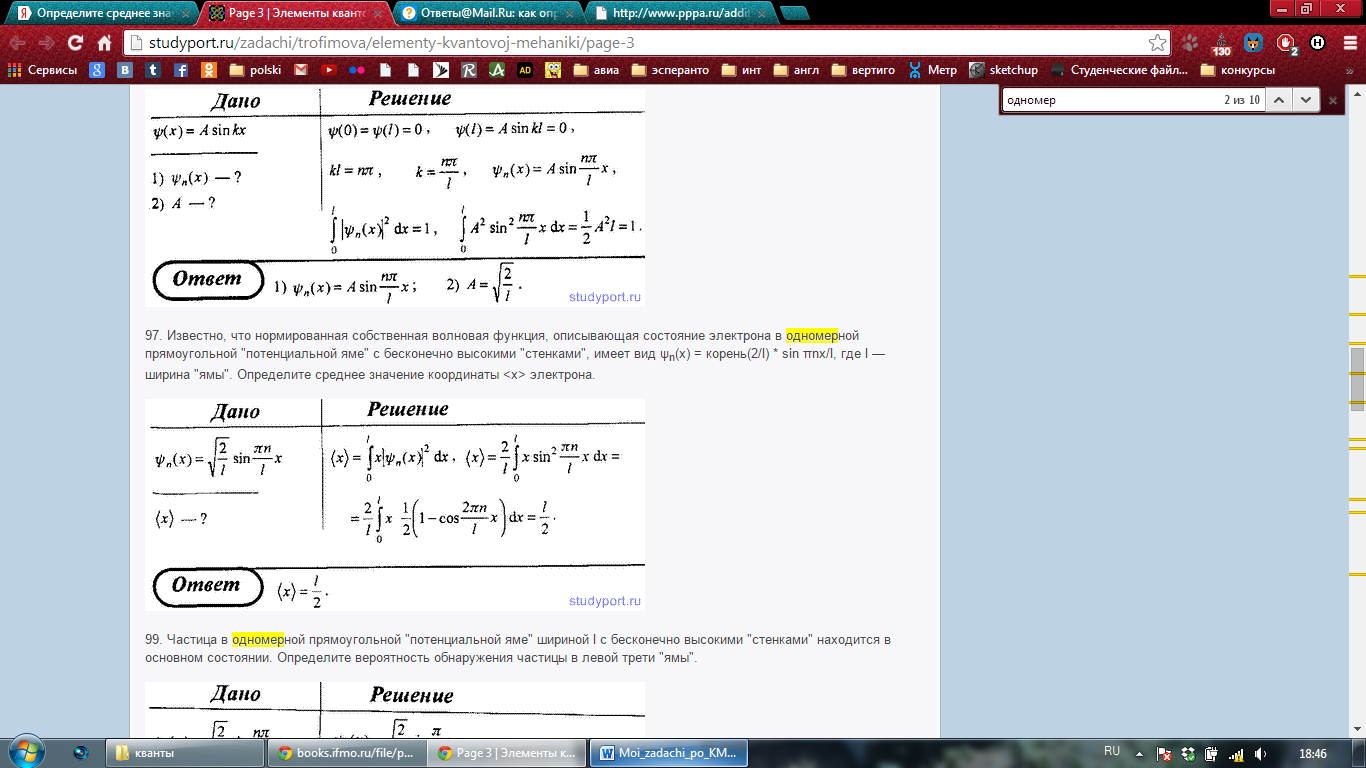
Задача 16.
Найти среднее значение кинетической энергии K электрона в одномерной яме шириной 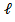 с бесконечно высокими “стенками”, если волновая функция имеет вид
с бесконечно высокими “стенками”, если волновая функция имеет вид
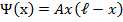 .
.
Ответ: 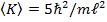
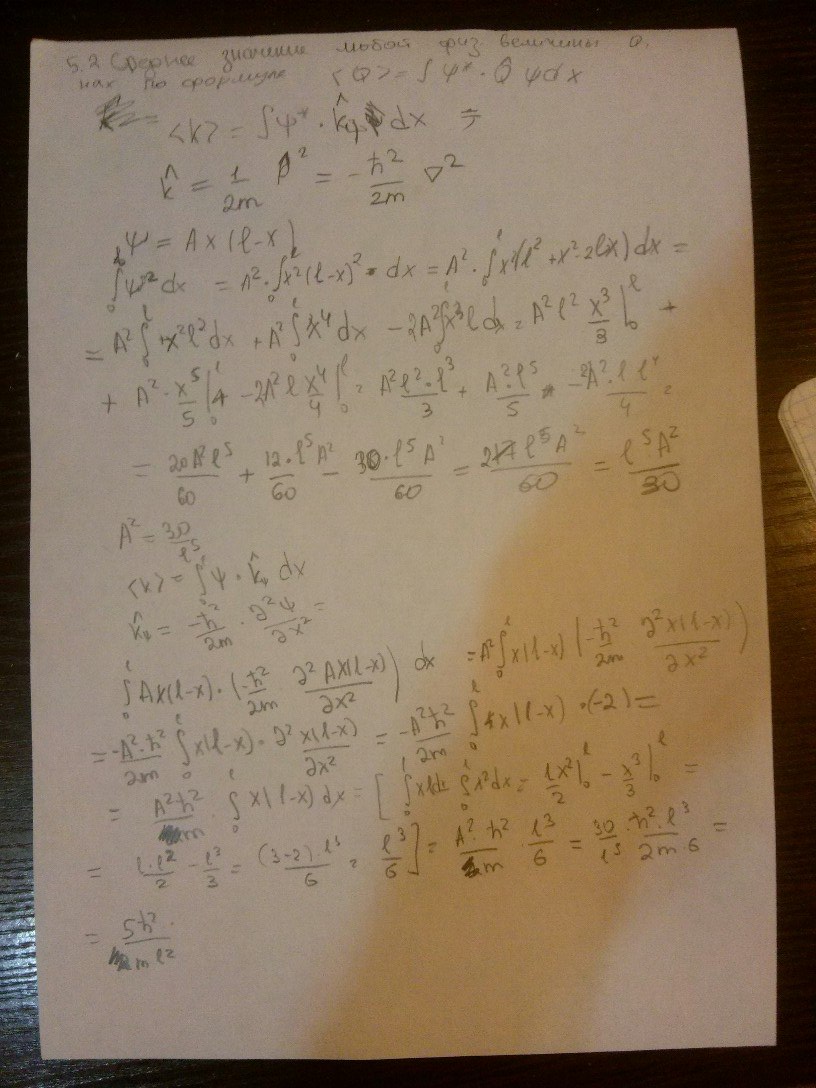
Задача 17.
Найти плотность состояний электрона 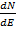 в двумерной яме с размерами
в двумерной яме с размерами 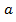 и b с бесконечно высокими “стенками”.
и b с бесконечно высокими “стенками”.
Ответ: 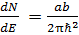

Задача 18.
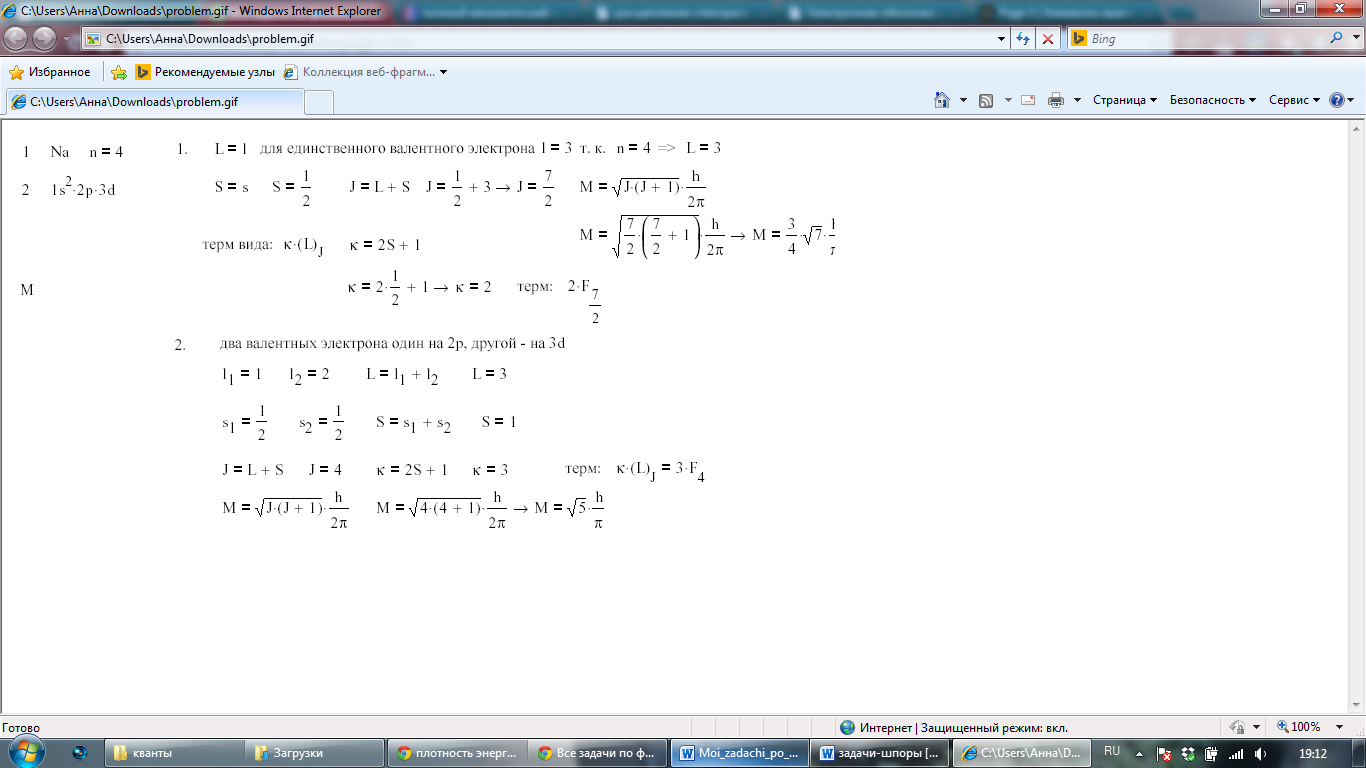
Найти максимально возможный полный механический момент и спектральный символ терма атома с электронной конфигурацией 1s22p3d
Ответ: 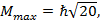 3F4
3F4
Решение:
Задача 19.
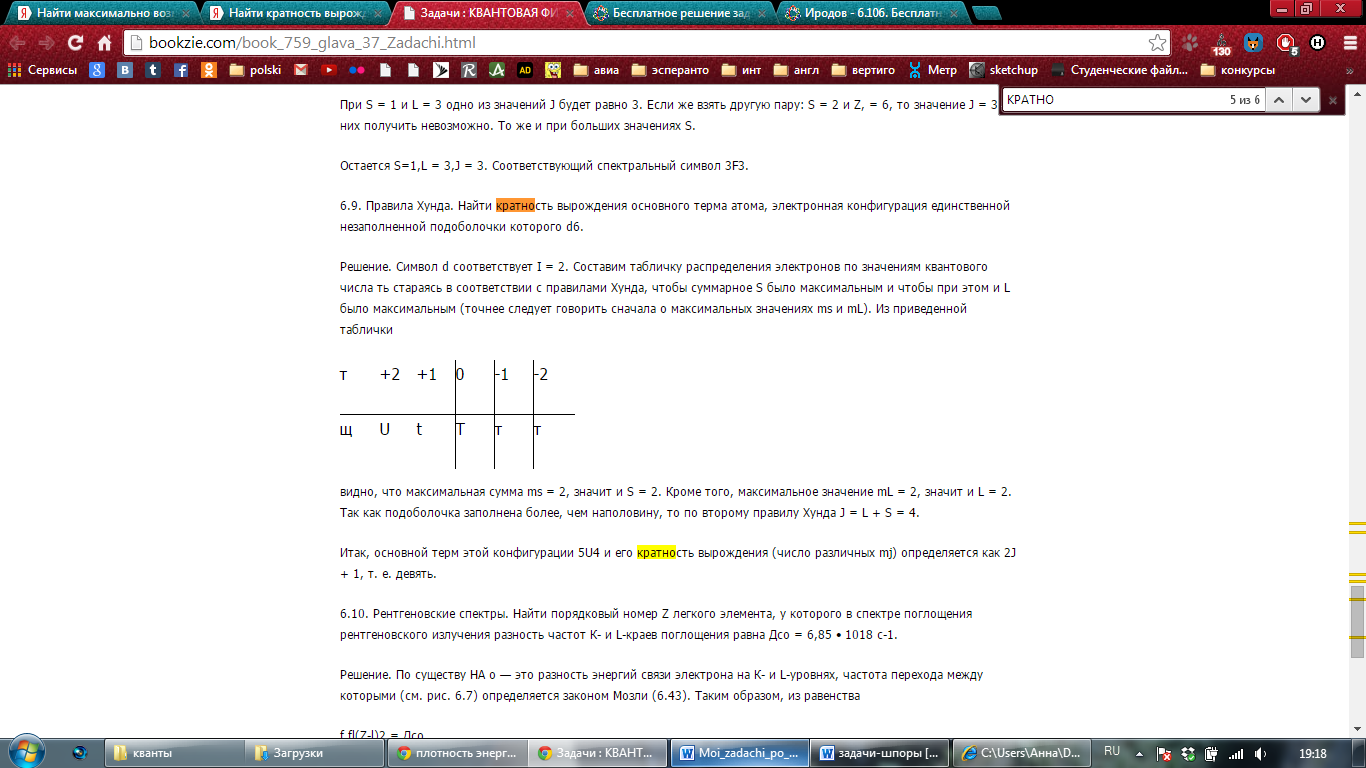
Найти кратность вырождения основного терма атома с единственной незаполненной подоболочкой d6 .
Ответ: J = 4, 2J+1 = 9
Решение:
Задача 20.
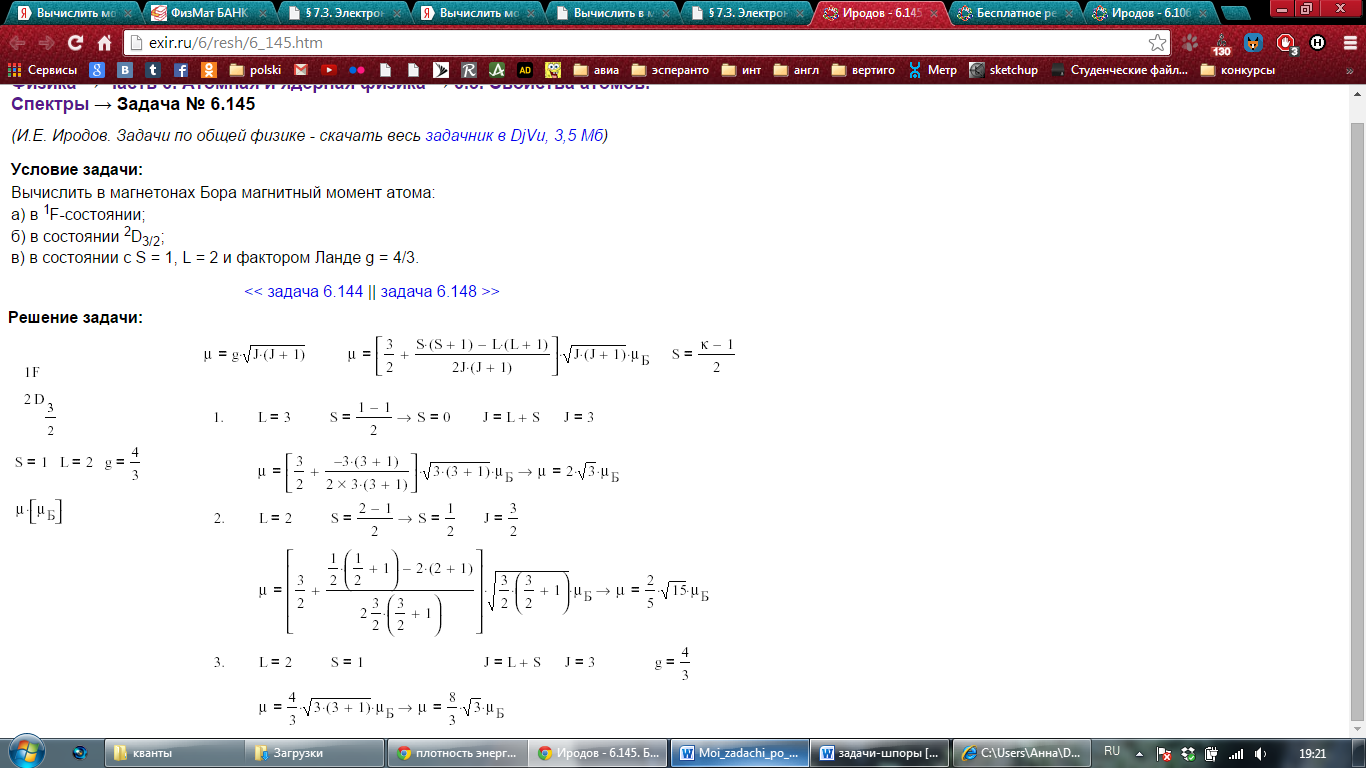
Вычислить модуль магнитного момента атома в состоянии с квантовыми числами
S=1, L=2 и фактором Ланде g =4/3.
Ответ: 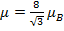
Решение:
Задача 21.
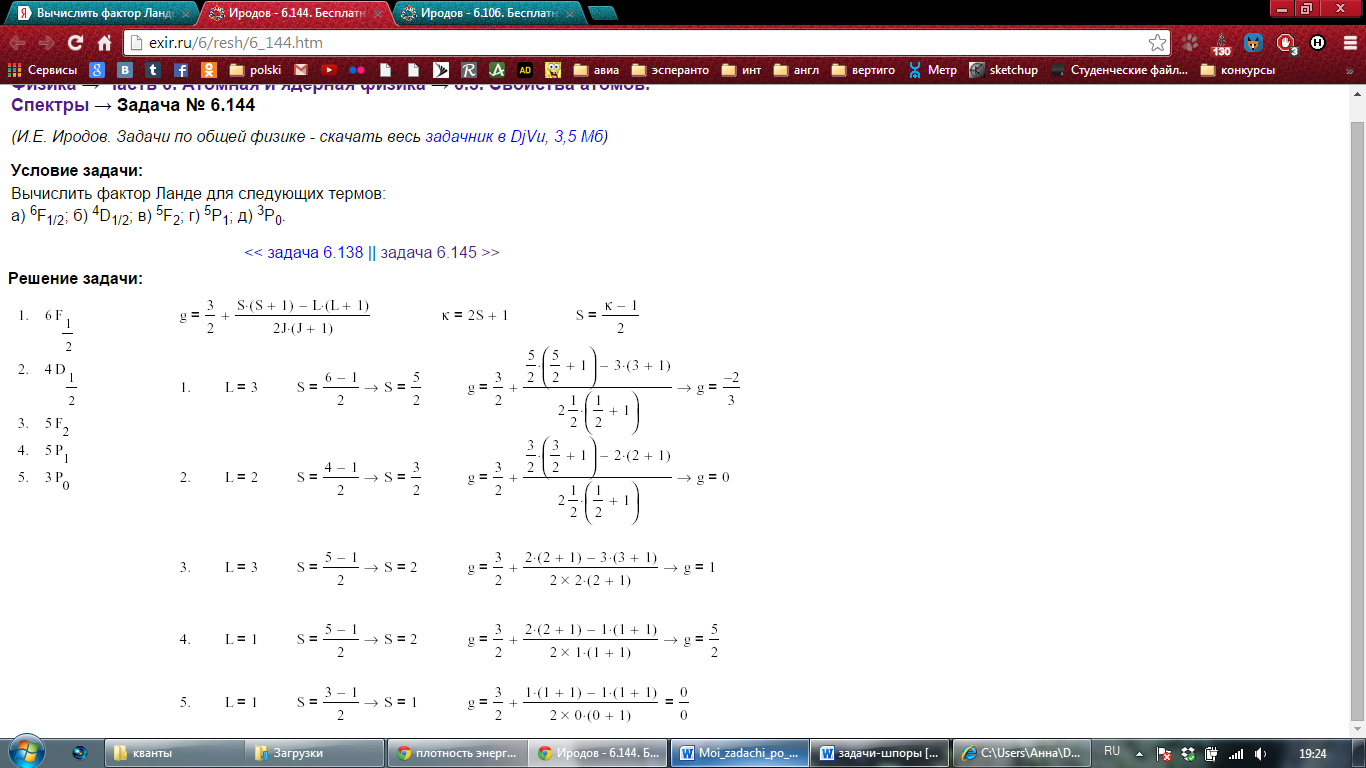
Вычислить фактор Ланде для термов: а) 3P0 ; б) 4D1/2 ; в) 6F1/2; г) 5P1.
Ответ: а) g = 0/0; б) g = 0; в) g = - 2/3; г) g = 5/2.
Элементы квантовой статистики
Задача 1
Покажите, что при очень малом параметре вырождения 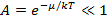 распределения Бозе - Эйнштейна и Ферми-Дирака переходят в распределение Максвелла-Больцмана.
распределения Бозе - Эйнштейна и Ферми-Дирака переходят в распределение Максвелла-Больцмана.
Решение:
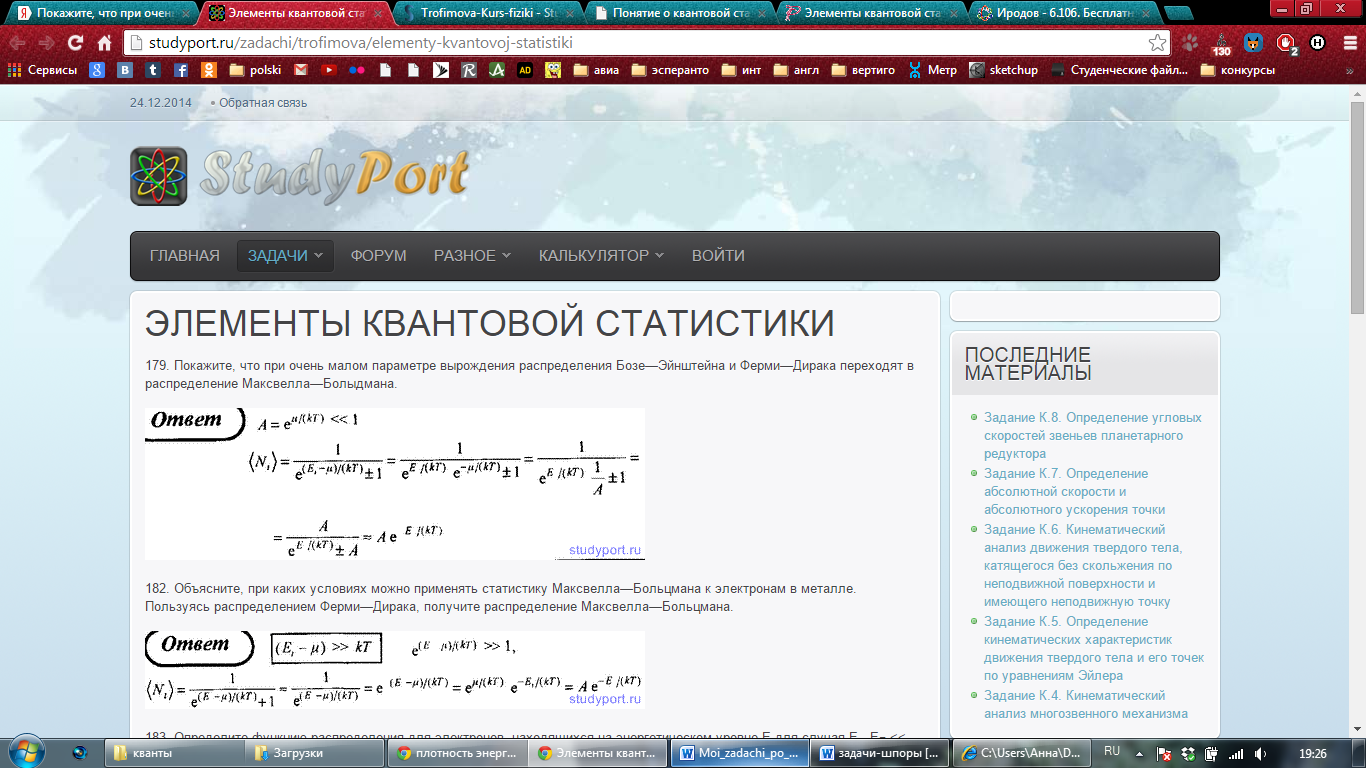
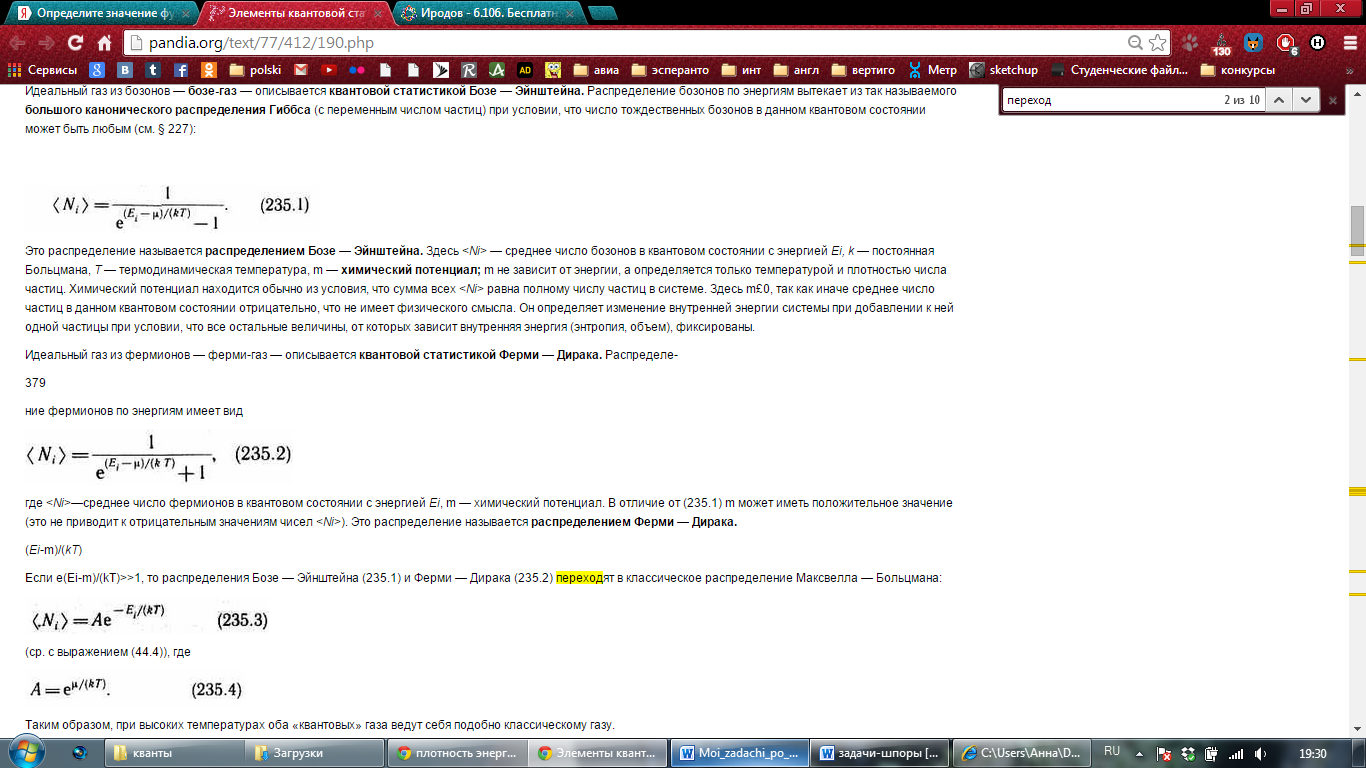
Немного из теории:
Задача 2
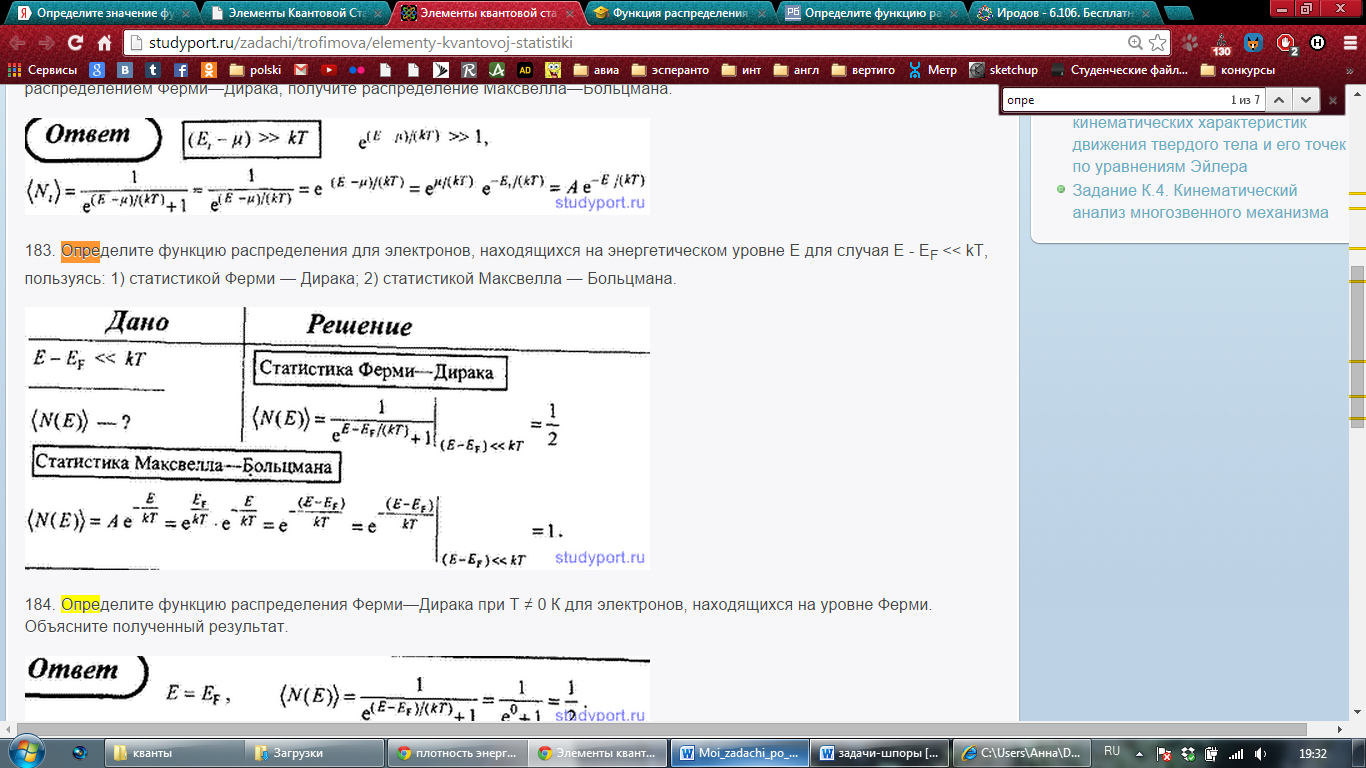
Определите значение функции распределения для электронов, находящихся на уровне Е для случая E - EF << kT, пользуясь: а) статистикой Ферми-Дирака; б) статистикой Максвелла-Больцмана.
Ответ: а) ½ ; б) 1.
|
из
5.00
|
Обсуждение в статье: Элементы квантовой статистики |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

