Четверти и октанты пространства

В § 4 было сказано, что плоскости 1 и 2 при пересечении образуют

четыре двугранных утла; их называют квадрантами или четвертями пространства.

На рис. 28 указан принятый порядок отсчета четвертей. Ось проекций делит

каждую из плоскостей 1 и 2 на "полы" (полуплоскости), условно обозначенные

1 и -- 1, 2 и -- 2. Если, например, точка расположена во второй

четверти, то горизонтальная проекция получается на -- 1, а фронтальная --

на 2.

В дальнейшем изложении за основу для построения чертежа точки в любой

из четырех четвертей мы будем брать рисунок по типу 13 (см. с. 16).

Считают, что зритель всегда находится в первой четверти (условно -- на

бесконечно большом расстоянии от 1 и от 2). Плоскости проекций считают

непрозрачными; поэтому видимы только точки, расположенные в первой четверти,

а также на полуплоскостях и 2.

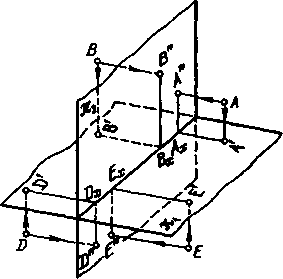
На рис. 13 дан чертеж для случая, когда точка расположена в первой

четверти (рис. 29). Если точка одинаково удалена от и 2, то А'АХ = А"АХ.

На рис. 30 показана точка В, расположенная во второй четверти, т. е.

над -- % и сзади 2 (рис. 29). Точка В ближе к 2, чем к -- ,: на чертеже

В'ВХ < В"ВЖ. Там же

 

III

 

Рис. 28 Рис. 29

 

показана точка С, одинаково удаленная от - ! и от 2: проекции С" и С'

совпадают между собой.

На рис. 31 дан чертеж для случая, когда точка D расположена в третьей

четверти. Горизонтальная проекция получается над осью проекций, фронтальная

проекция -- под осью проекций. Так как D'DX > D"DX, то точка D

расположена от -- 2 дальше, чем от -- .

На рис. 32 даны точки и F, расположенные в четвертой четверти. Точка

Е ближе к ,, чем к -- 2 (рис. 29): Е"ЕХ < Е'ЕХ. Точка F одинаково

удалена от -- 2 и от ..: F'FX = F"FX.

На рис. 33 в системе ,, 2 изображены точки А и В, расположенные

симметрично относительно пл. ,. На чертеже (рис. 33, справа) горизонтальные

проекции

 

 

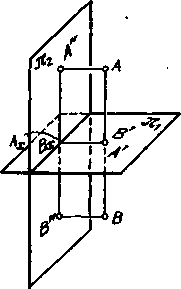
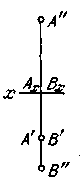
Рис. 31 Рис. 33

 

таких точек совпадают одна с другой, фронтальные же проекции находятся

на равных расстояниях от оси проекций: А"АХ = В"ВХ.

 

В практике черчения имеет место применение первой и третьей четвертей

пространства. Подробнее см. в § 41.

 

На рис. 27 было показано, что плоскости координат в своем пересечении

образуют восемь трехгранных углов -- восемь октантов. Нумерация октантов

указана на рис.27. Как видно из рис.28, четверти нумеруются как I--IV

октанты. Применяя для отсчета координат точки систему знаков, указанную на рис.

27, получим следующую таблицу:

	Знаки координат		Знаки координат
		У				У	z
I	+	+	+	V		+	+
	+	_	+	VI	--	--	+
III	+	_	_	VII	_	_	_
IV	+	+	-	VIII	-	+	-

 

 

Например, точка (--20; + 15; --18) находится в восьмом октанте.

Совмещение плоскостей производится согласно рис. 34, т. е. пл. 3 отводится

против часовой стрелки, если смотреть на пл. ! по направлению от +z к О.

 

Рис. 34

На рис. 34 даны также чертежи точек: А, расположенной в первом октанте,

и С, расположенной в седьмом октанте; проекции одной и той же точки не могут

наложиться одна на другую. Для остальных октантов две или все три (для

второго и восьмого октантов) проекции одной и той же точки могут оказаться

наложенными друг на друга.

5. Положение прямой относительно плоскостей проекций. Особые случаи положения прямой.

Прямая линия может занимать относительно плоскостей проекций особые

(иначе, частные) положения. Рассмотрим их по следующим двум признакам:

А. Прямая параллельна одной плоскости проекций.

Б. Прямая параллельна двум плоскостям проекций.

В первом случае одна проекция отрезка прямой равна самому отрезку. Во

втором случае две проекции отрезка равны ему1).

 

А. Прямая параллельна одной плоскости проекций

 

1. Прямая параллельна пл. , (рис. 50). В таком случае фронтальная

проекция прямой параллельна оси проекций и горизонтальная проекция отрезка

этой прямой равна самому отрезку: А'В'=АВ. Такая прямая называется

горизонтальной.

Если, например, проекция А"В" совпадает с осью проекций, то отрезок АВ

расположен в пл. , 2).

 

 

Рис. 50

 

Рис. 51

 

2. Прямая параллельна пл. 2 (рис. 51). В таком случае ее

горизонтальная проекция параллельна оси проекций и фронтальная проекция

отрезка этой прямой равна самому отрезку: C"D" = CD. Такая прямая называется

фронтальной.

Если, например, проекция C'D' совпадает с осью проекций, то это

соответствует положению отрезка CD в самой пл. 2.

 

') Все это, конечно, с учетом масштаба чертежа.

2) На рис. 50 справа дан чертеж без указания оси проекций.

То же сделано на рис. 51.

 

3. Прямая параллельна пл. 3 (рис. 52). В таком случае горизонтальная и

фронтальная проекции прямой располагаются на одном перпендикуляре к оси

проекций Ох и профильная проекция этой прямой равна самому отрезку: E"F" =

EF. Такая прямая называется профильной.

 

 

Рис. 52 Рис. 53

Можно ли считать, что на чертежах, подобных указанным на рис. 50 и 51,

изображены отрезки именно прямых линий? Да; доказательство такое же, как для

прямой общего положения (рис. 46).

Если же на чертеже в системе 5 2 обе проекции перпендикулярны к оси

проекций, то проецирующие плоскости, проведенные через E'F и E"F", сливаются

в одну и оригиналом может быть не только прямая линия, но и некоторая

плоская кривая (рис. 53).

 

Б. Прямая параллельна двум плоскостям проекций

 

 

1. Прямая параллельна плоскостям 1 и 2 (рис. 54), т. е.

перпендикулярна к пл. 3. Проекция на пл. 3 представит собой точку.

2. Прямая параллельна плоскостям , и 3 (рис. 55), т. е.

перпендикулярна к пл. 2. Проекция на пл. 3 представляет собой отрезок

прямой, равный CD'.

 

 

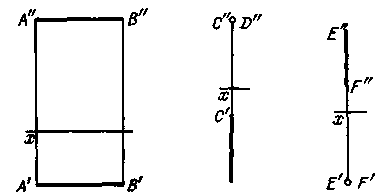
Рис. 54 Рис. 55 Рис. 56 Рис. 57

3. Прямая параллельна плоскостям 2 и 3 (рис. 56), т. е.

перпендикулярна к

пл. nt. Проекция на пл. 3 представит собой отрезок, параллельный и

равный E"F".

На рис. 57 дано наглядное изображение положения рассмотренных прямых').') Для этих прямых встречается название "проецирующие прямые".

 

 

Рис. 58 Рис. 59

Обычно строятся проекции отрезков прямой линии с указанием концевых

точек отрезка. Если же по каким-либо причинам показывают некоторую

неопределенную часть прямой линии, то практически тоже показывают отрезок

линии, но не обозначают концевых точек этого отрезка. При этом можно

пользоваться обозначением каждой проекции только одной буквой, относя ее к

какой-либо точке прямой (рис. 58): "прямая, проходящая через точку А".

Обратим внимание на чертеж слева на рис. 59. Относительно прямой,

изображенной на нем, можно сказать лишь то, что она проходит через точку L и

параллельна пл. jtj, но в остальном положение этой прямой не определяется.

Определенность была бы внесена горизонтальной проекцией, т. е. проекцией на

плоскости, по отношению к которой прямая параллельна.

Если же мы имеем дело с прямой, заданной двумя своими точками

(например, с отрезком прямой, заданным своими концами), то можно точно

определить положение этой прямой и в том случае, если не задана ее проекция

на плоскости, параллельной этой прямой. Так, например, если дан отрезок АВ

прямой (рис. 59, справа), то мы можем установить не только параллельность

этой прямой по отношению к пл. -, но и то, что точка A данной прямой более

удалена от пл. 2, чем точка В.

 

6. Взаимное положение прямых.

 

Прямые могут быть параллельными, пересекающимися и скрещивающимися.

У параллельных прямых проекции параллельны. Для способа проекций с числовыми отметками этого определения недостаточно, так как отсутствуют другие проекции, определяющие положение прямых. Две прямые в проекциях с числовыми отметками параллельны в том случае, если:

1) проекции их параллельны;

2)интервалы или уклоны равны;

3) отметки возрастают в одном направлении.

Параллельные прямые могут быть заданы проекциями двух точек, направлением (указано стрелкой) и уклоном, который должен быть одинаковым для обеих прямых.

Пересекающиеся прямые имеют общую точку, а следовательно, проекции прямых имеют общую точку с одинаковой отметкой. Определить, пересекаются ли прямые, можно следующим образом: проградуировать прямые, и если в точке пересечения они имеют одну и ту же отметку, то прямые пересекаются. В противном случае прямые скрещиваются.

7. Положение плоскости относительно плоскостей проекций. Следы плоскостей.

Любая, произвольно взятая в пространстве, плоскость может занимать общее или частное положение. Плоскостью общего положения называется плоскость, которая не перпендикулярна ни к одной из плоскостей проекций (см. рис. 5.2). Все остальные плоскости (кроме плоскостей проекций) относятся к плоскостям частного положения подразделяются на проецирующие плоскости и плоскости уровня. |Проецирующей называется плоскость, перпендикулярная к одной из плоскостей проекций. Например, горизонтально-проецирующая плоскость перпендикулярна к горизонтальной плоскости проекции П1 (рис. 5.3).

 

Конструирование зубчатых колес Конические зубчатые колеса. Теоретическая механика

Горизонтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с горизонтальным следом 1. Угол 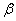, который образуется между плоскостями и П2, проецируется на П1 без искажения. Фронтальный след 2 перпендикулярен к оси x. Фронтально-проецирующая плоскость ( ) перпендикулярна к фронтальной плоскости П2 (рис. 5.4).

Фронтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с фронтальным следом плоскости 2. Угол , который образуется между заданной плоскостью и П1, проецируется на П2 без искажения. Горизонтальный след плоскости 1 перпендикулярен к оси x.

 

Профильно-проецирующая плоскость Т (T1, T2) перпендикулярна к профильной плоскости проекции П3 (рис. 5.5).

 

Профильные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с профильным

 

следом плоскости Т3. Углы и 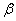, которые образуются между заданной плоскостью и плоскостями проекций П1 П2 ( = T^П1; = Т^П2), проецируются на плоскость П3 без искажений. Горизонтальный и фронтальный следы плоскости параллельны оси х.

Профильнопроецирующая плоскость может проходить через ось x: (рис. 5.6).

Следы этой плоскости 1 = 2 совпадают друг с другом и с осью x, поэтому не определяют положение плоскости. Необходимо кроме следов задать в плоскости точку (рис. 5.6). В частном случае эта плоскость может быть биссекторной плоскостью. Угол ° = °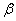, а точка А равноудалена от плоскостей проекций П1 П2.

Плоскостью уровня называется плоскость, перпендикулярная одновременно к двум плоскостям проекций и параллельная третьей. Таких плоскостей три разновидности (рис. 5.7):

горизонтальная плоскость уровня перпендикулярна к П2, П3 и параллельна П1 (рис. 5.7, а);

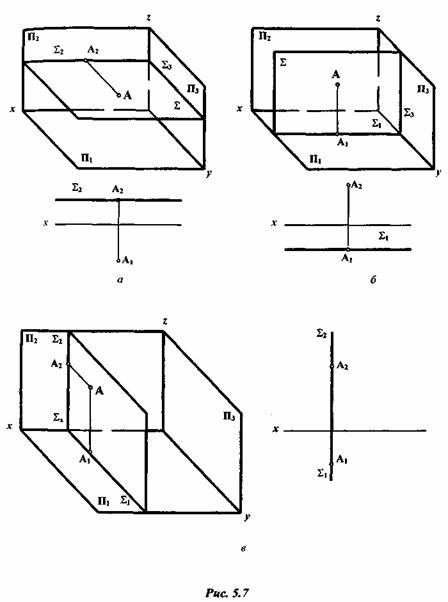фронтальная плоскость уровня перпендикулярна к П1 П3 и параллельна П2 (рис. 5.7, б);

профильная плоскость уровня перпендикулярна к П1 П2 и параллельна П3 (рис. 5.7 в).

 

Из определения плоскостей уровня следует, что одна из проекций точки, линии, фигуры, принадлежащих этим плоскостям, будет совпадать с одноименным следом плоскости уровня, а другая проекция будет натуральной величиной этих геометрических образов.

В техническом рисовании аксонометрические изображения начинают с нанесения аксонометрических осей, выполняя все операции от руки на глаз, без применения чертежных инструментов. Аксонометрические рисунки правильных треугольников и шестиугольников показаны на рис.. Длины соответствующих отрезков с ортогонального изображения многоугольника переносятся на аксонометрические оси.

 

8. Прямые особого положения в плоскости (главные линии плоскости).

К прямым, занимающим особое положение в плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций. Эти линии называют главными линиями плоскости.

Горизонталь— прямая, лежащая в плоскости и параллельная плоскости проекций Н. На рисунке 3.15 проекции горизонтали проведены через проекции с', с точки С и l', 1 точки 1 прямой АВплоскости, заданной проекциями точки С и прямой АВ. Фронтальная проекция с’, l' горизонтали параллельна оси х.

Фронталь — прямая, лежащая в плоскости и параллельная плоскости проекций V. На рисунке 3.16 проекции фронтали проведены через проекции l', 1 и 2’, 2 точек 1 и 2 проекций a'b', ab, c'd', cdпараллельных прямых АВ и СВ заданной

плоскости. Горизонтальная проекция 1—2 фронтали параллельна оси х.

Линиями наибольшего наклона плоскости к плоскостям Н, V и W называют прямые, лежащие в ней и перпендикулярные или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым. Соответственно определяется наклон плоскости к плоскостям Н, V или W.

Рассмотрим линию наибольшего наклона к плоскости Н, называемую линией ската.

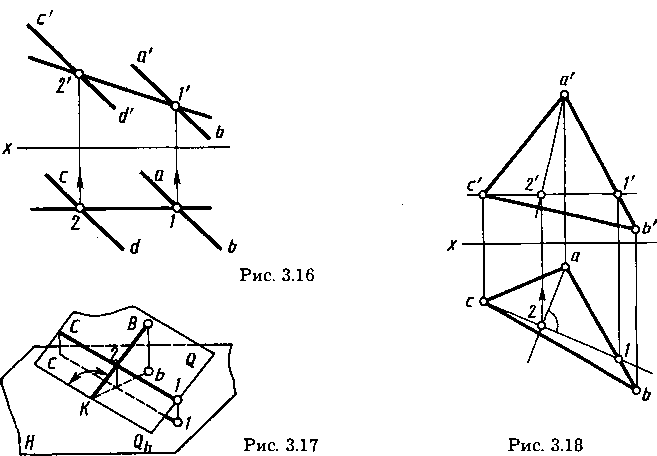Линия ската ВК плоскости Q и горизонталь С—1 показаны на рисунке 3.17: BK перпендикулярнаQ_h. Согласно правилам проецирования прямого угла (см. 1.3, 2.4, рис. 1.10, 2.16) bКперпендикулярна Q и с—1. Поэтому угол ВКb есть линейный угол двугранного угла, образованного плоскостями Q и Н. Следовательно, линия ската плоскости может служить для определения угла наклона этой плоскости к плоскости проекций Н. На рисунке 3.18 линия ската А— 2 в плоскости треугольника с проекциями а'b'с’, abc проведена перпендикулярно к горизонтали с проекциями с'l', с—1.

Вначале на горизонтальной проекции а проведен перпендикуляр а—2 к проекции с—1горизонтали, построена фронтальная проекция 2' точки 2 и через нее проведена фронтальная проекция а’2’ линии ската.

 

Угол между линией ската и ее горизонтальной проекцией является линейным углом между плоскостью, которой принадлежит линия ската, и плоскостью проекций Н.

9. Пересечение двух плоскостей.

Пересечение двух плоскостей, заданных треугольниками ABC и DEF.

Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии - точка M.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии - точка N.
Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.

Для определения видимости используем конкурирурющие точки:
на фронтальной плоскости проекций - 1"≡6"; 1`, 6` и 5"≡ 7"; 5`, 7` - будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций - 8`≡9`; 8", 9" и 10`≡ 11`; 10", 11" - будет видна вершина Cс прилегающими сторонами до линии пересечения.