 |
Главная |
Доказательство этой теоремы выходит за пределы курса
|
из
5.00
|
Лекция 2
12. Линейные подпространства.
Определение 12.1. Подмножество 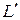 линейного пространства L называется линейным подпространством, если
линейного пространства L называется линейным подпространством, если
 ,
,  .
.
Справедливость аксиом линейного пространства для L  прямо вытекает из их справедливости в L. Таким образом, каждое линейное подпространство само является линейным пространством.
прямо вытекает из их справедливости в L. Таким образом, каждое линейное подпространство само является линейным пространством.
Пусть дано некоторое множество P векторов в линейном пространстве L. Совокупность всевозможных линейных комбинаций, каждая из которых составлена из конечного числа векторов, принадлежащих P, называется линейной оболочкой множества P. Покажем, что линейная оболочка L  множества P является линейным подпространством.
множества P является линейным подпространством.
В самом деле, если  , то
, то  ,
,  , где все
, где все  и
и 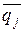 принадлежат P. Тогда
принадлежат P. Тогда 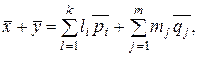
 , т.е. сумма векторов
, т.е. сумма векторов  и произведение вектора
и произведение вектора  на число
на число 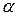 снова являются линейными комбинациями конечного числа векторов из P.
снова являются линейными комбинациями конечного числа векторов из P.
Приведем еще два примера линейных подпространств.
1. Сумма двух геометрических векторов в одной плоскости и произведение вектора на число лежат в той же плоскости. Следовательно, множество всех геометрических векторов в плоскости есть линейное подпространство множества всех геометрических векторов в пространстве.
2. Рассмотрим однородную систему линейных уравнений с n неизвестными. Каждое решение такой системы есть элемент пространства  . Так как сумма двух решений однородной системы и произведение решения на число являются решениями той же системы, то совокупность всех решений однородной системы линейных уравнений с n неизвестными есть линейное подпространство пространства
. Так как сумма двух решений однородной системы и произведение решения на число являются решениями той же системы, то совокупность всех решений однородной системы линейных уравнений с n неизвестными есть линейное подпространство пространства  .
.
13. Евклидово пространство.
Понятия длины вектора и угла между ними в линейном пространстве введем с помощью скалярного произведения, которое определим аксиоматически.
Определение 13.1. Числовая функция вида L×L→R, сопоставляющая каждой паре векторов  некоторое вещественное число, обозначаемое
некоторое вещественное число, обозначаемое  , называется скалярным произведением векторов
, называется скалярным произведением векторов 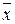 и
и 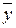 , если выполнены следующие четыре условия (аксиомы):
, если выполнены следующие четыре условия (аксиомы):
1)  ; 2)
; 2) 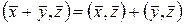 ;
;
3) 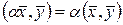 ; 4)
; 4) 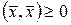 ,
,
причем  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Определение 13.2. Конечномерное линейное пространство с заданным скалярным произведением называется евклидовым и обозначается E.
Приведем примеры евклидовых пространств.
1) В пространстве  скалярное произведение векторов
скалярное произведение векторов 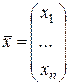 и
и 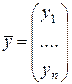
зададим формулой  . Нетрудно проверить, что так определенное скалярное произведение удовлетворяет всем перечисленным выше четырем аксиомам. Следовательно, пространство
. Нетрудно проверить, что так определенное скалярное произведение удовлетворяет всем перечисленным выше четырем аксиомам. Следовательно, пространство  превращается в n-мерное евклидово, которое называется n-мерным координатным евклидовым пространством и обозначается
превращается в n-мерное евклидово, которое называется n-мерным координатным евклидовым пространством и обозначается 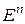 .
.
2) В линейном пространстве геометрических векторов на плоскости или в пространстве скалярное произведение задается формулой
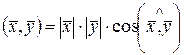 .
. 
В разделе «Векторная алгебра» показывается, что так определенное скалярное произведение удовлетворяет всем четырем аксиомам скалярного произведения.
Определение 13.3. Длиной вектора 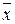 в евклидовом пространстве называется число
в евклидовом пространстве называется число 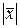 , определяемое формулой
, определяемое формулой
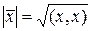 . (13.1)
. (13.1)
Углом между двумя ненулевыми векторами 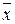 и
и 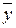 называется число
называется число 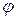 , удовлетворяющее условию
, удовлетворяющее условию
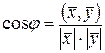 . (13.2)
. (13.2)
В силу четвертой аксиомы длина вектора есть вещественное неотрицательное число, равное нулю тогда и только тогда, когда вектор нулевой. Определение (13.2) будет корректным лишь в том случае, когда 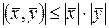 или
или
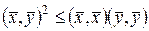 . (13.3)
. (13.3)
Неравенство (13.3) носит название неравенства Буняковского. Докажем его справедливость. При любых 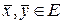 и любых
и любых  в силу аксиом скалярного произведения имеем:
в силу аксиом скалярного произведения имеем:
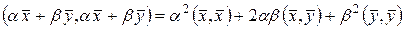 ,
,
так как  то
то
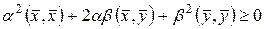 . (13.4)
. (13.4)
Полагая в (13.4) 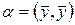 ,
, 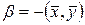 получим
получим 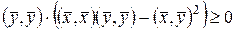 .
.
Отсюда при 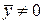 вытекает доказываемое неравенство. В случае
вытекает доказываемое неравенство. В случае 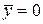 обе части неравенства (13.3) равны нулю.
обе части неравенства (13.3) равны нулю.
Определение 13.4. Векторы 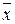 и
и 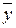 в евклидовом пространстве называются ортогональными, если
в евклидовом пространстве называются ортогональными, если 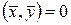 .
.
Нулевой вектор по определению считается ортогональным любому вектору. Заметим, что ортогональность геометрических векторов означает их перпендикулярность.
Определение 13.5. Система векторов 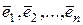 в евклидовом пространстве называется ортонормированной, если
в евклидовом пространстве называется ортонормированной, если
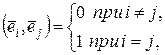
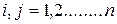 . (13.5)
. (13.5)
Теорема 13.1. Ортонормированная система векторов линейно независима.
Доказательство. Пусть 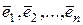 - ортонормированная система векторов. Рассмотрим равенство
- ортонормированная система векторов. Рассмотрим равенство 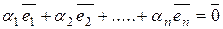 . Обе части этого равенства умножим скалярно на
. Обе части этого равенства умножим скалярно на 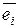 ,
,  . В силу (13.5) все слагаемые кроме i-го обратятся в нуль и мы получим
. В силу (13.5) все слагаемые кроме i-го обратятся в нуль и мы получим 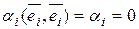 .
.
Таким образом, каждая равная нулю линейная комбинация векторов 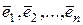 - тривиальная, т.е. система векторов
- тривиальная, т.е. система векторов 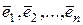 линейно независима.
линейно независима.
Определение 13.6. Ортонормированным базисом в n-мерном евклидовом пространстве  называется любая ортонормированная система n векторов.
называется любая ортонормированная система n векторов.
Пусть в n-мерном евклидовом пространстве  задан ортонормированный базис
задан ортонормированный базис  и пусть
и пусть 
 . Тогда в силу аксиом скалярного произведения
. Тогда в силу аксиом скалярного произведения 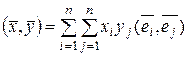 . Отсюда на основании (13.5)
. Отсюда на основании (13.5)
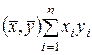 , (13.6)
, (13.6)
т.е. в ортонормированном базисе скалярное произведение двух векторов равно сумме по парных произведений их соответствующих координат. Из (13.6) непосредственно следует
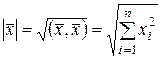 ,
,
т.е. в ортонормированном базисе длина вектора равна корню квадратному из суммы квадратов его координат.
Пусть в n-мерном евклидовом пространстве  задана линейно независимая система n векторов
задана линейно независимая система n векторов 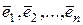 . Построим n векторов
. Построим n векторов  по формулам:
по формулам:  ,
,  , где
, где 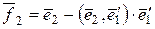 ,
,  , где
, где 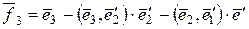 , …,
, …, 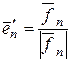 где
где 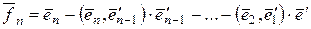 .
.
Доказывается, что система векторов  ортонормированная. Указанный метод построения ортонормированной системы векторов по заданной линейно независимой системе векторов называется ортогонализацией этой системы.
ортонормированная. Указанный метод построения ортонормированной системы векторов по заданной линейно независимой системе векторов называется ортогонализацией этой системы.
Рассмотрим в n-мерном евклидовом пространстве  два ортонормированных базиса
два ортонормированных базиса  и
и  . Пусть
. Пусть  - матрица перехода от базиса
- матрица перехода от базиса 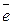 к базису
к базису  . Согласно (11.7)
. Согласно (11.7)
 ,
, 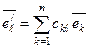
 . Отсюда в силу (13.5)
. Отсюда в силу (13.5)

или опять же в силу (13.5)
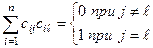 . (13.7)
. (13.7)
В матричных обозначениях равенства (13.7) переписывается в виде
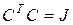 , (13.8)
, (13.8)
где 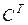 - транспонированная матрица С, а J - единичная матрица. По определению обратной матрицы равенство (13.8) равносильно
- транспонированная матрица С, а J - единичная матрица. По определению обратной матрицы равенство (13.8) равносильно
 .
.
Определение 13.7. Матрица С, удовлетворяющая условию (13.8), называется ортогональной.
Простейшим примером ортогональной матрицы является 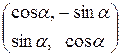 .
.
Итак, ортогональные матрицы и только они могут служить матрицами перехода от одного ортонормированного базиса к другому.
14. Линейные преобразования.
Рассмотрим линейное пространство L и преобразование Ā в этом пространстве, сопоставляющее каждому вектору 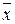 из L некоторый вектор
из L некоторый вектор  из того же пространства. Образ
из того же пространства. Образ  вектора
вектора 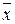 при преобразовании Ā будем обозначать
при преобразовании Ā будем обозначать  .
.
Определение 14.1. Преобразование Ā линейного пространства L называется линейным, если для любых векторов  и любого числа
и любого числа
 выполняются условия
выполняются условия
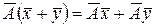 ,
, 
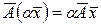 . (14.1)
. (14.1)
Нетрудно проверить, что при линейном преобразовании линейная комбинация векторов переходит в линейную комбинацию их образов с теми же коэффициентами. Преобразование вида 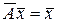 является линейным. Оно называется тождественным и обозначается
является линейным. Оно называется тождественным и обозначается 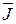 .
.
Приведем еще один пример линейного преобразования. Производная от многочлена есть многочлен меньший степени. Поэтому дифференцирование является преобразованием в линейном пространстве многочленов степени не выше заданного числа n. Это преобразование линейное, так как производная суммы равна сумме производных и постоянный множитель выносится за знак производной.
Выберем в n-мерном линейном пространстве  базис
базис  . Каждый вектор
. Каждый вектор  может быть разложен по этому базису, т.е. представлен в виде
может быть разложен по этому базису, т.е. представлен в виде 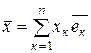 , где
, где 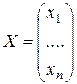 - координатный столбец вектора
- координатный столбец вектора 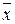 в базис
в базис  . По свойству (14.1) линейного преобразования
. По свойству (14.1) линейного преобразования
 . (14.2)
. (14.2)
Разлагая каждый из векторов  по базису
по базису  , получим
, получим
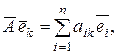
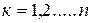 . (14.3)
. (14.3)
Подстановка (14.3) в (14.2) даст
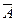
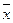
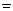

Отсюда по определению координат
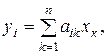
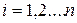 , (14.4)
, (14.4)
где 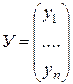 - координатный столбец вектора
- координатный столбец вектора 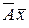 в базисе
в базисе  . Обозначим
. Обозначим
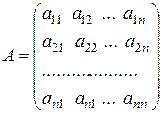 . (14.5)
. (14.5)
В матричной форме равенства (14.4) запишутся в виде
 . (14.6)
. (14.6)
Матрица А называется матрицей линейного преобразования  в базисе
в базисе 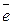 . Столбцы матрицы А есть координатные столбцы образов векторов
. Столбцы матрицы А есть координатные столбцы образов векторов 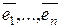 при преобразовании
при преобразовании  . Итак, в заданном базисе линейное преобразование
. Итак, в заданном базисе линейное преобразование  определяется своей матрицей (14.5). Само линейное преобразование задается формулами (14.4). В случае тождественного преобразования для каждого вектора
определяется своей матрицей (14.5). Само линейное преобразование задается формулами (14.4). В случае тождественного преобразования для каждого вектора 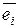 ,
, 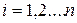 имеем
имеем  . Поэтому тождественное преобразование в каждом базисе определяется единичной матрицей J.
. Поэтому тождественное преобразование в каждом базисе определяется единичной матрицей J.
Результат последовательного выполнения двух линейных преобразований  и
и 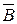 называется их произведением и обозначается
называется их произведением и обозначается 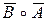 . Пусть в некотором базисе линейные преобразования
. Пусть в некотором базисе линейные преобразования  и
и 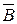 имеют соответственно матрицы А и В.
имеют соответственно матрицы А и В.
Теорема 14.1. Произведение 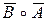 имеет матрицу
имеет матрицу 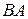 . Для доказательства обозначим через Х, У, Z соответственно координатные столбцы векторов
. Для доказательства обозначим через Х, У, Z соответственно координатные столбцы векторов 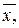
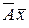 ,
, 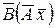 . Тогда по формуле (14.6)
. Тогда по формуле (14.6) 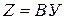 , или
, или  , или по свойству произведения матриц
, или по свойству произведения матриц 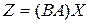 , т.е. произведение
, т.е. произведение 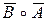 определяется матрицей
определяется матрицей 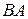 .
.
Определение 14.2. Линейное преобразование  в евклидовом пространстве E называется ортогональным, если
в евклидовом пространстве E называется ортогональным, если 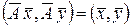 для любых
для любых  .
.
Таким образом, ортогональное преобразование сохраняет скалярное произведение, а, следовательно, длины векторов и углы между ними. Можно показать, что в любом ортонормированном базисе ортогональное преобразование имеет ортогональную матрицу. Примером ортогонального преобразования в 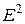 является
является
 ,
,
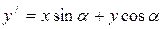 .
.
15. Собственные векторы и собственные значения линейного преобразования.
Определение 15.1. Ненулевой вектор 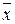 называется собственным вектором линейного преобразования
называется собственным вектором линейного преобразования  , если существует такое число
, если существует такое число 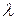 , что
, что
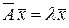 . (15.1)
. (15.1)
При этом число 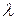 называется собственным значением линейного преобразования
называется собственным значением линейного преобразования  .
.
Зададим в пространстве  какой-либо базис
какой-либо базис  . Пусть в этом базисе линейное преобразование
. Пусть в этом базисе линейное преобразование  имеет матрицу
имеет матрицу
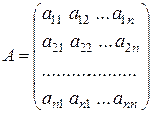 , (15.2)
, (15.2)
а вектор 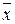 - координатный столбец
- координатный столбец 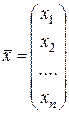 . В силу (14.4) равенство (15.1) равносильно соотношениям
. В силу (14.4) равенство (15.1) равносильно соотношениям 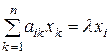 ,
, 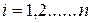 или в развернутом виде
или в развернутом виде
 . (15.3)
. (15.3)
Таким образом, координаты собственного вектора являются ненулевым решением однородной системы линейных уравнений (15.3). Эта система имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы (15.3) равен нулю, т.е.
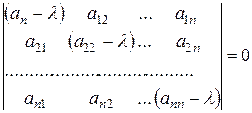 . (15.4)
. (15.4)
Доказывается, что уравнение (15.4) не зависит от выбора базиса. Оно называется характеристическим уравнением линейного преобразования  .
.
Раскрыв определитель в левой части (15.4), получим уравнение n-ой степени относительно 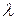 . Оно имеет ровно n корней. Собственные значения линейного преобразования
. Оно имеет ровно n корней. Собственные значения линейного преобразования  совпадают с корнями уравнения (15.4). Каждому собственному значению
совпадают с корнями уравнения (15.4). Каждому собственному значению 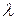 соответствует бесконечное множество собственных векторов. Все они находятся из системы (15.3).
соответствует бесконечное множество собственных векторов. Все они находятся из системы (15.3).
Матрица вида 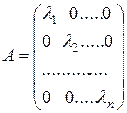 , где
, где 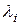 - некоторые числа, называется диагональной.
- некоторые числа, называется диагональной.
Теорема 15.1. Матрица линейного преобразования  в базисе
в базисе  имеет диагональный вид с собственными значениями на главной диагонали тогда и только тогда, когда все векторы базиса есть собственные вектора преобразования
имеет диагональный вид с собственными значениями на главной диагонали тогда и только тогда, когда все векторы базиса есть собственные вектора преобразования  .
.
Доказательство. i-ый столбец матрицы линейного преобразования  есть координатный столбец вектора
есть координатный столбец вектора  . В этом столбце i-ый элемент равен
. В этом столбце i-ый элемент равен 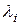 , а остальные элементы равны нулю тогда и только тогда, когда
, а остальные элементы равны нулю тогда и только тогда, когда 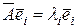 ? т.е. вектор
? т.е. вектор 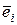 - собственный для линейного преобразования
- собственный для линейного преобразования 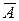 .
.
Определение 15.2. Линейное преобразование 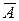 евклидова пространства E называется симметрическим, если для любых векторов
евклидова пространства E называется симметрическим, если для любых векторов  выполняется условие.
выполняется условие.
 . (15.5)
. (15.5) 
Зададим в n-мерном евклидовом пространстве  ортонормированный базис. Пусть в этом базисе линейное преобразование
ортонормированный базис. Пусть в этом базисе линейное преобразование  имеет матрицу (15.2), а векторы
имеет матрицу (15.2), а векторы 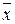 и
и 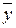 - координатные столбцы
- координатные столбцы 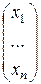 и
и 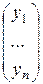 соответственно. В силу (14.4) координатными столбцами векторов
соответственно. В силу (14.4) координатными столбцами векторов 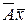 и
и  будут
будут
 и
и 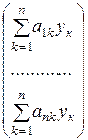
соответственно. Отсюда по формуле (13.6)
 ,
,  . (15.6)
. (15.6)
Подстановка выражений (15.6) в условие (15.5) дает
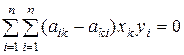 .
.
В силу произвольности 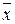 и
и 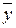 отсюда следует
отсюда следует
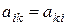 ,
, 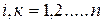 . (15.7)
. (15.7)
Условие (15.7) равносильно
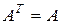 . (15.8)
. (15.8)
Определение 15.2. Матрица  , удовлетворяющая условию (15.8), называется симметрической.
, удовлетворяющая условию (15.8), называется симметрической.
Таким образом, доказано, что матрица симметрического преобразования в любом ортонормированном базисе является симметрической.
Собственные значения и собственные векторы симметрического преобразования обладают рядом важных и интересных свойств, к изложению которых мы и перейдем.
Теорема 15.2. Все собственные значения симметрического преобразования вещественные.
Доказательство этой теоремы выходит за пределы курса.
Теорема 15.3. Собственные векторы симметрического преобразования  , соответствующие разным собственным значениям, ортогональны.
, соответствующие разным собственным значениям, ортогональны.
Доказательство. Пусть 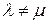 и
и  ,
, 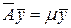 . Тогда
. Тогда
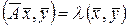 ,
,  . (15.9)
. (15.9)
Из (15.5) в силу (15.9) следует 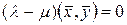 , отсюда
, отсюда 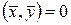 , что и требовалось доказать.
, что и требовалось доказать.
Доказывается, что в n-мерном евклидовом пространстве  существует ортонормированный базис из собственных векторов симметрического преобразования
существует ортонормированный базис из собственных векторов симметрического преобразования  . Для нахождения указанного базиса следует вычислить собственные значения преобразования А и для каждого значения найти соответствующий собственный вектор. В случае простого корня характеристического уравнения собственный вектор остается только нормировать, т.е. разделить на его длину. Для корня кратности r надо найти r линейно независимых собственных вектора, соответствующих фундаментальной системе из r решений однородной системы линейных уравнений (15.3). Эти векторы следует ортогонализировать и нормировать.
. Для нахождения указанного базиса следует вычислить собственные значения преобразования А и для каждого значения найти соответствующий собственный вектор. В случае простого корня характеристического уравнения собственный вектор остается только нормировать, т.е. разделить на его длину. Для корня кратности r надо найти r линейно независимых собственных вектора, соответствующих фундаментальной системе из r решений однородной системы линейных уравнений (15.3). Эти векторы следует ортогонализировать и нормировать.
16. Квадратичные формы.
Рассмотрим в линейном пространстве L числовую функцию 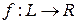 , сопоставляющую каждому вектору
, сопоставляющую каждому вектору  некоторое вещественное число
некоторое вещественное число  . Числовая функция
. Числовая функция 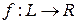 называется линейной формой, если для любых
называется линейной формой, если для любых  и любого
и любого 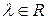 выполняются следующие условия
выполняются следующие условия
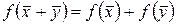 ,
, 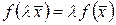 .
.
Далее, рассмотрим числовую функцию  , сопоставляющую каждой паре векторов
, сопоставляющую каждой паре векторов  некоторое действительное число
некоторое действительное число 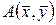 . Числовая функция
. Числовая функция  называется билинейной формой, если при фиксированном
называется билинейной формой, если при фиксированном 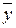 она является линейной формой по
она является линейной формой по 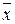 , а при фиксированном
, а при фиксированном 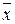 - линейной формой по
- линейной формой по 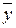 . Билинейная форма
. Билинейная форма 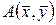 называется симметрической, если
называется симметрической, если 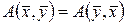 при любых
при любых  . Простейшим примером билинейной формы является скалярное произведение векторов.
. Простейшим примером билинейной формы является скалярное произведение векторов.
Пусть 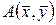 - симметрическая билинейная форма в линейном пространстве L.
- симметрическая билинейная форма в линейном пространстве L.
Определение 16.1. Числовая функция 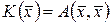 , полученная из
, полученная из 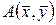 при
при 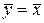 , называется квадратичной формой в пространстве L.
, называется квадратичной формой в пространстве L.
Пусть в пространстве  задан базис
задан базис  и пусть
и пусть 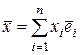 ,
, 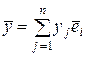 . В силу свойств билинейной формы
. В силу свойств билинейной формы

или
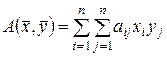 , (16.1)
, (16.1)
где  . При этом в силу симметричности билинейной формы
. При этом в силу симметричности билинейной формы 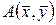
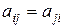 . (16.2)
. (16.2)
Полагая в (16.1) 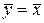 получим следующее представление квадратичной формы
получим следующее представление квадратичной формы 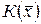 в базисе
в базисе 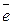 :
:
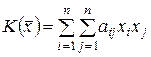 . (16.3)
. (16.3)
Матрица
 (16.4)
(16.4)
называется матрицей квадратичной формы 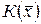 в заданном базисе
в заданном базисе 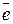 . Согласно (16.2) матрица (16.4) является симметрической. Итак, в заданном базисе каждой квадратичной форме
. Согласно (16.2) матрица (16.4) является симметрической. Итак, в заданном базисе каждой квадратичной форме 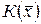 соответствует симметрическая матрица (16.4) и, обратно, каждой симметрической матрице (16.4) соответствует квадратичная форма
соответствует симметрическая матрица (16.4) и, обратно, каждой симметрической матрице (16.4) соответствует квадратичная форма 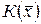 , представление которой в заданном базисе
, представление которой в заданном базисе 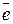 имеет вид (16.3).
имеет вид (16.3).
Определение 16.2. Квадратичная форма 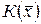 называется положительно (отрицательно) определенной, если
называется положительно (отрицательно) определенной, если 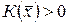
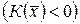 для всех
для всех 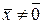 , и знакопеременной, если существуют такие
, и знакопеременной, если существуют такие  , что
, что 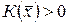 ,
, 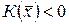 .
.
Ниже будет указан критерий, то которому можно судить о принадлежности квадратичной формы к одному из указанных типов
Определители
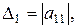
 …………
………… 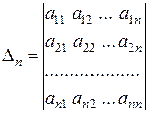
называются угловыми минорами матрицы (16.4).
Теорема 16.1. (Критерий Сильвестра) Для того чтобы, квадратичная форма 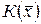 была положительно (отрицательно) определенной необходимо и достаточно, чтобы все угловые миноры ее матрицы были положительны (знаки угловых миноров чередовались, причем
была положительно (отрицательно) определенной необходимо и достаточно, чтобы все угловые миноры ее матрицы были положительны (знаки угловых миноров чередовались, причем 
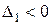 ).
).
Пусть в некотором базисе  квадратичная форма
квадратичная форма 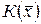 имеет вид
имеет вид
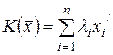 . (16.5)
. (16.5)
Выражение (16.5) называется каноническим видом квадратичной формы. Далее, будем рассматривать квадратичные формы в евклидовом пространстве. Линейное преобразование  , матрица которого в любом ортонормированном базисе совпадает с матрицей квадратичной формы
, матрица которого в любом ортонормированном базисе совпадает с матрицей квадратичной формы 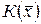 , называется присоединенным к
, называется присоединенным к 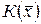 .
.
В силу симметрическости матрицы 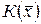 присоединенное к
присоединенное к 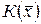 преобразование
преобразование  будет симметрическим. Согласно результатам §15 в евклидовом пространстве
будет симметрическим. Согласно результатам §15 в евклидовом пространстве  существует ортонормированный базис
существует ортонормированный базис  из собственных векторов преобразования
из собственных векторов преобразования  , в котором матрица этого преобразования имеет диагональный вид с собственными значениями
, в котором матрица этого преобразования имеет диагональный вид с собственными значениями  на главной диагонали. Если
на главной диагонали. Если 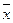
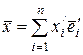 , то в базисе
, то в базисе  квадратичная форма
квадратичная форма 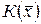 приводится к сумме квадратов (16.5). При этом в силу (11.9) соответствующее преобразование координат определяется формулой
приводится к сумме квадратов (16.5). При этом в силу (11.9) соответствующее преобразование координат определяется формулой
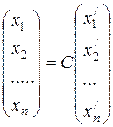 , (16.6)
, (16.6)
где столбцами матрицы С являются координатные столбцы векторов  в исходном базисе
в исходном базисе  . Так как переход от одного ортонормированного базиса к другому осуществляется с помощью ортогональной матрицы, то преобразование (16.6) в пространстве
. Так как переход от одного ортонормированного базиса к другому осуществляется с помощью ортогональной матрицы, то преобразование (16.6) в пространстве  - ортогональное.
- ортогональное.
Пример. Квадратичную форму  в евклидовом пространстве привести к каноническому виду.
в евклидовом пространстве привести к каноническому виду.
Решение. Матрица квадратичной формы есть
 .
.
Составляем характеристическое уравнение
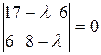 .
.
Его корни  ,
, 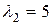 . Соответствующие
. Соответствующие 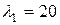 и
и 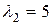 собственные векторы, присоединенные к
собственные векторы, присоединенные к 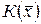 линейного преобразования
линейного преобразования  , находятся из уравнений
, находятся из уравнений 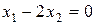 и
и  соответственно. Это векторы
соответственно. Это векторы  и
и  , где
, где 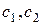 - любые числа. После нормировки, т.е. деления этих векторов на их длины, получаем ортонормированный базис из векторов
- любые числа. После нормировки, т.е. деления этих векторов на их длины, получаем ортонормированный базис из векторов 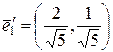 ,
,  . В этом базисе квадратичная форма
. В этом базисе квадратичная форма 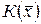 имеет канонический вид
имеет канонический вид  . Соответствующее преобразование координат есть
. Соответствующее преобразование координат есть  или
или  ,
, 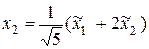 .
.
|
из
5.00
|
Обсуждение в статье: Доказательство этой теоремы выходит за пределы курса |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

