 |
Главная |
Урок №37. Системы линейных уравнений с параметром. Тест №6
|
из
5.00
|
Рассмотрим систему из двух линейных уравнений с двумя неизвестными:  . Напомним, что каждое линейное уравнение задает на плоскости прямую. Система имеет единственное решение, если эти прямые пересекаются, бесконечно много решений, если они совпадают, и не имеет решений, если они параллельны. Если коэффициенты системы — известные числа, то очень просто решить систему, либо показать, что она не имеет решений. Но, если коэффициенты системы содержат параметр, возникают некоторые сложности. Мы сформулируем условия, которым должны удовлетворять коэффициенты системы, чтобы система 1)
. Напомним, что каждое линейное уравнение задает на плоскости прямую. Система имеет единственное решение, если эти прямые пересекаются, бесконечно много решений, если они совпадают, и не имеет решений, если они параллельны. Если коэффициенты системы — известные числа, то очень просто решить систему, либо показать, что она не имеет решений. Но, если коэффициенты системы содержат параметр, возникают некоторые сложности. Мы сформулируем условия, которым должны удовлетворять коэффициенты системы, чтобы система 1)  имела единственное решение; 2) имела бесконечно много решений; 3)
имела единственное решение; 2) имела бесконечно много решений; 3)  не имела решений.
не имела решений.
Чтобы система  имела единственное решение, необходимо и достаточно, чтобы выполнялось условие
имела единственное решение, необходимо и достаточно, чтобы выполнялось условие  . Чтобы понять происхождение этого условия, попытаемся решить систему. Умножим первое уравнение на
. Чтобы понять происхождение этого условия, попытаемся решить систему. Умножим первое уравнение на 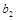 , а второе на
, а второе на 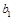 и вычтем из первого второе. Получим уравнение
и вычтем из первого второе. Получим уравнение  . Если
. Если  , то, поделив обе части на это выражение, мы находим единственное значение
, то, поделив обе части на это выражение, мы находим единственное значение 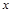 . Если
. Если  , а
, а  , то, очевидно, решений нет. В случае, когда
, то, очевидно, решений нет. В случае, когда  и
и  , то возможно и отсутствие решений (например, система
, то возможно и отсутствие решений (например, система  ), и бесконечно много решений (например, система
), и бесконечно много решений (например, система  ). Данные условия можно истолковать геометрически следующим образом. Если
). Данные условия можно истолковать геометрически следующим образом. Если  , то
, то  , т. е. коэффициенты прямых
, т. е. коэффициенты прямых  и
и  при переменных не пропорциональны, прямые имеют разный наклон и пересекаются. Если же
при переменных не пропорциональны, прямые имеют разный наклон и пересекаются. Если же 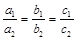 (это выполняется при условии
(это выполняется при условии  ,
,  ,
,  ), то уравнения
), то уравнения  и
и  задают одну прямую, поскольку одно получается из другого умножением на число, например,
задают одну прямую, поскольку одно получается из другого умножением на число, например,  и
и  . При
. При  прямые имеют одинаковый наклон, но не совпадают, т. е. параллельны.
прямые имеют одинаковый наклон, но не совпадают, т. е. параллельны.
1. Найти, при каких  система
система 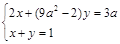 не имеет решений. Решение. Должно выполняться условие
не имеет решений. Решение. Должно выполняться условие 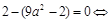

 . Внимание! Полученные значения нужно проверить. Подставим в систему
. Внимание! Полученные значения нужно проверить. Подставим в систему  и получим систему
и получим систему  . Но эта система имеет бесконечно много решений. Подставим в систему
. Но эта система имеет бесконечно много решений. Подставим в систему 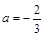 и получим систему
и получим систему  . Эта система действительно не имеет решений. Ответ:
. Эта система действительно не имеет решений. Ответ:  .
.
2. Найти, при каких  система
система  имеет бесконечно много решений. Решение. Должно выполняться условие
имеет бесконечно много решений. Решение. Должно выполняться условие 
 . Полученные значения нужно проверить. Подставим в систему
. Полученные значения нужно проверить. Подставим в систему  и получим систему
и получим систему 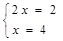 . Но эта система не имеет решений. Подставим в систему
. Но эта система не имеет решений. Подставим в систему  и получим систему
и получим систему  . Эта система действительно имеет бесконечно много решений. Ответ: 4.
. Эта система действительно имеет бесконечно много решений. Ответ: 4.
3. Изобразить на плоскости множество всех точек  таких, что при данных значениях
таких, что при данных значениях  система
система  имеет ненулевое решение. Решение. Поскольку решение (0; 0) эта система имеет, то по условию она должна иметь бесконечно много решений. Значит, должно выполняться условие
имеет ненулевое решение. Решение. Поскольку решение (0; 0) эта система имеет, то по условию она должна иметь бесконечно много решений. Значит, должно выполняться условие 
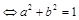 . Причем при любых таких значениях
. Причем при любых таких значениях  система имеет бесконечно много решений (не иметь решений она не может). Итак, данное множество — это окружность единичного радиуса с центром в точке (0; 0).
система имеет бесконечно много решений (не иметь решений она не может). Итак, данное множество — это окружность единичного радиуса с центром в точке (0; 0).
4. Найти числа  такие, что система
такие, что система  имеет бесконечно много решений, причем
имеет бесконечно много решений, причем  — одно их них. Решение. Подставим значения
— одно их них. Решение. Подставим значения  в систему и добавим условие
в систему и добавим условие  :
:  . Преобразуя систему, получаем
. Преобразуя систему, получаем  . Решения этой системы
. Решения этой системы 
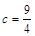 и
и 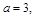
 . Производим проверку и убеждаемся, что оба ответа подходят. Ответ:
. Производим проверку и убеждаемся, что оба ответа подходят. Ответ: 
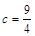 ;
;  .
.
5. При каких  системы
системы  и
и  равносильны? Решение. Первая система при
равносильны? Решение. Первая система при  не имеет решений. Найдем, при каких значениях
не имеет решений. Найдем, при каких значениях  вторая система не имеет решений. Рассмотрим равенство
вторая система не имеет решений. Рассмотрим равенство  , в данном случае
, в данном случае  . Проверкой убеждаемся, что при
. Проверкой убеждаемся, что при  вторая система решений не имеет, значит, системы равносильны. При
вторая система решений не имеет, значит, системы равносильны. При  вторая система имеет вид
вторая система имеет вид  и имеет бесконечно много решений (а первая решений не имеет). При
и имеет бесконечно много решений (а первая решений не имеет). При 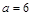 первая система имеет бесконечно много решений, а вторая — одно решение, значит, они не равносильны. Ответ: –2.
первая система имеет бесконечно много решений, а вторая — одно решение, значит, они не равносильны. Ответ: –2.
6. При каких значениях  все решения
все решения 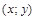 системы
системы  удовлетворяют условию
удовлетворяют условию  ? Решение. Выразим
? Решение. Выразим 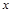 из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:  ,
, 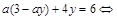
 . Прежде, чем выражать из этого уравнения
. Прежде, чем выражать из этого уравнения  , нужно рассмотреть случай, когда
, нужно рассмотреть случай, когда 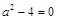 . Если
. Если  , то получаем
, то получаем  , здесь решений нет. Если
, здесь решений нет. Если  , то получаем
, то получаем  . Это означает, что
. Это означает, что  можно взять произвольным. Таким образом, при
можно взять произвольным. Таким образом, при  решением системы является любая пара чисел вида
решением системы является любая пара чисел вида  . Но неверно, что все они удовлетворяют условию
. Но неверно, что все они удовлетворяют условию  , значит,
, значит,  в ответ не войдет. Пусть теперь
в ответ не войдет. Пусть теперь  , тогда можно уравнение
, тогда можно уравнение 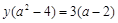 сократить на
сократить на  выразить
выразить 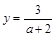 . Затем находим
. Затем находим 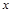 :
: 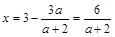 . Запишем условия
. Запишем условия 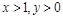 в виде системы:
в виде системы: 

 . Учитывая, что
. Учитывая, что  , получаем
, получаем  . Ответ:
. Ответ:  .
.
Домашнее задание
7. При каких значениях  система
система 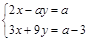 имеет бесконечно много решений? Ответ: –6.
имеет бесконечно много решений? Ответ: –6.
8. При каких значениях  система
система  имеет бесконечно много решений? Ответ: 3.
имеет бесконечно много решений? Ответ: 3.
9. При каких значениях параметра  система
система  имеет а) единственное решение; б) бесконечно много решений; в) не имеет решений? Ответ: а)
имеет а) единственное решение; б) бесконечно много решений; в) не имеет решений? Ответ: а)  ; б)
; б)  ; в)
; в)  .
.
10. При каких значениях  система
система 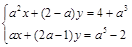 не имеет решений? Ответ: 1.
не имеет решений? Ответ: 1.
11. При каких значениях  система
система  не имеет решений? Ответ: –4.
не имеет решений? Ответ: –4.
12. Числа  таковы, что система
таковы, что система  имеет единственное решение,
имеет единственное решение,  . Найти эти числа. Ответ:
. Найти эти числа. Ответ: 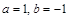
13. При каких значениях  системы
системы 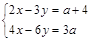 и
и  равносильны? Ответ: –3; 3.
равносильны? Ответ: –3; 3.
Тест №6
1. Результат упрощения выражения 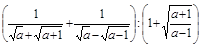 , где
, где  , равен 1)
, равен 1)  ; 2)
; 2) 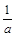 ; 3)
; 3)  ; 4)
; 4)  .
.
2. Число 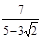 является корнем квадратного уравнения
является корнем квадратного уравнения  ; 2)
; 2)  ; 3)
; 3) 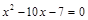 ;
;  .
.
3. Среднее арифметическое корней уравнения  равно 1)
равно 1)  ; 2)
; 2)  ; 3) 1; 4) 0.
; 3) 1; 4) 0.
4. Сумма всех целых решений неравенства  равна 1) –4; 2) –5; 3) –2; 4) таких решений бесконечно много.
равна 1) –4; 2) –5; 3) –2; 4) таких решений бесконечно много.
5. Число различных корней уравнения  равно 1) 2; 2) 1; 3) 3; 4) 4.
равно 1) 2; 2) 1; 3) 3; 4) 4.
6. Прямые  и
и 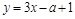 пересекаются в точке, лежащей на оси Oy, если a равно 1)
пересекаются в точке, лежащей на оси Oy, если a равно 1) 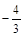 ; 2)
; 2)  ; 3) 1; 4)
; 3) 1; 4)  .
.
7. Сумма корней уравнения  равна
равна  1) 4; 2)
1) 4; 2)  5; 3) –2; 4) 6.
5; 3) –2; 4) 6.
8. Система неравенств 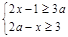 имеет единственное решение при значении a, равном 1) 7; 2) –3; 3)
имеет единственное решение при значении a, равном 1) 7; 2) –3; 3) 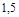 ; 4) 6.
; 4) 6.
9. Множество значений функции  не пересекается с областью определения функции
не пересекается с областью определения функции 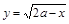 , если 1)
, если 1)  ; 2)
; 2)  ;
; 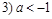 ; 4) всегда не пересекается.
; 4) всегда не пересекается.
10. Число целочисленных решений системы  равно 1) 0; 2) 2; 3) 8; 4) 10.
равно 1) 0; 2) 2; 3) 8; 4) 10.
11.
|
 равно: 1)
равно: 1) 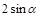 ; 2)
; 2) 
 ;
;  ; 4)
; 4)  .
.
12. Уравнение 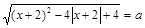 имеет четыре корня при
имеет четыре корня при 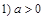 ; 2) a Î (0; 2); 3) a Î (2; 4); 4) a Î (2; +¥).
; 2) a Î (0; 2); 3) a Î (2; 4); 4) a Î (2; +¥).
13. Корни уравнения 

 образуют множество 1)
образуют множество 1)  ;
;  ; 3)
; 3)  ; 4)
; 4) 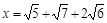 .
.
14. Выбрать число, ближайшее к одному из корней уравнения 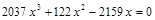 : 1) 0,5; 2) 2; 3) –0,5; 4) –1.
: 1) 0,5; 2) 2; 3) –0,5; 4) –1.
15. Параболы на рисунке заданы уравнениями (1)  ,
,  . При этом выполняются неравенства:
. При этом выполняются неравенства: 


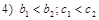 .
. 
|
из
5.00
|
Обсуждение в статье: Урок №37. Системы линейных уравнений с параметром. Тест №6 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


