 |
Главная |
Молекулярно-кинетическая теория идеальных газов
|
из
5.00
|
Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К практическим занятиям
По курсу общей физики
Уфа 2005
Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К практическим занятиям
По курсу общей физики
Уфа 2005
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям
по курсу общей физики
Уфа 2005
Составители С.А. Шатохин, Э.В. Сагитова
УДК [539.19+536](07)
ББК [22.36+22.317](Я7)
Основы молекулярной физики и термодинамики: Методические указания к практическим занятиям по курсу общей физики. / Уфимск. гос. авиац. техн. ун-т; Сост.: С.А. Шатохин, Э.В. Сагитова -Уфа, 2005. - 32 c.
Приведены примеры решения различных типов задач по темам практических занятий раздела «Основы молекулярной физики и термодинамики». Предназначены для студентов 1 и 2 курсов.
Библиогр.: 5 назв.
Рецензенты: А.С. Краузе
Э.З. Якупов
© Уфимский государственный
авиационный
 |
технический университет, 2005
Содержание
Введение........................................................................................................... 4
Основные формулы........................................................................................ 5
Примеры решения задач................................................................................ 9
1. Молекулярно-кинетическая теория идеальных газов ........................ 9
2. Основы термодинамики.......................................................................... 15
Список литературы....................................................................................... 32
Введение
Практические занятия являются одной из важнейших компонент учебного процесса по физике. Они способствуют приобщению студентов к самостоятельной работе, учат анализировать изучаемые физические явления, использовать на практике полученные теоретические знания.
Предназначены для студентов, изучающих раздел курса общей физики «Основы молекулярной физики и термодинамики». В методических указаниях представлены примеры решения типичных задач разной степени трудности. Решения сопровождаются необходимыми примерами и комментариями. Задачи систематизированы по основным темам раздела. Приведены основные формулы, облегчающие усвоение алгоритмов решения задач.
Основы молекулярной физики и термодинамики
Основные формулы
Количество вещества 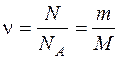 ,
,
где
N – число молекул,
NA – постоянная Авогадро,
m – масса вещества,
M – молярная масса.
Уравнение Менделеева- Клайперона
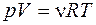 ,
,
где
р – давление газа,
V – его объем,
R – молярная газовая постоянная,
T – термодинамическая температура.
Уравнение молекулярно – кинетической теории газов
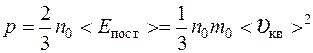 ,
,
где
n0 – концентрация молекул,
<Eпост> – средняя кинетическая энергия поступательного движения молекул,
m0 – масса молекулы,
<υкв> – средняя квадратичная скорость.
Средняя кинетическая энергия молекулы
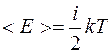 ,
,
где
i – число степеней свободы,
k – постоянная Больцмана.
Внутренняя энергия идеального газа
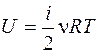 .
.
Скорости молекул:
средняя квадратичная 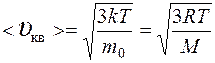 ,
,
средняя арифметическая 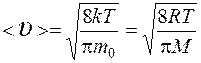 ,
,
наиболее вероятная 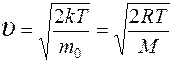 .
.
Средняя длина свободного пробега молекулы
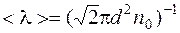 ,
,
где d – эффективный диаметр молекулы.
Среднее число столкновений молекулы в единицу времени
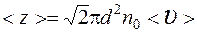 .
.
Уравнение диффузии
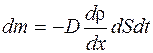 ,
,
где
D – коэффициент диффузии,
Ρ – плотность,
dS – элементарная площадка, перпендикулярная к оси Х.
Уравнение теплопроводности
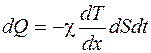 ,
,
где χ – коэффициент теплопроводности.
Сила внутреннего трения 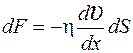 ,
,
гдеη – динамическая вязкость.
Коэффициент диффузии 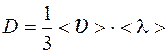 .
.
Вязкость (динамическая) 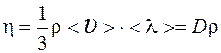 .
.
Теплопроводность 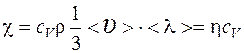 ,
,
где сV - удельная изохорная теплоемкость.
Молярная теплоемкость идеального газа:
Изохорная 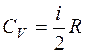 ,
,
Изобарная 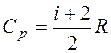 .
.
Первое начало термодинамики
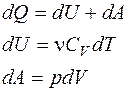
Работа расширения газа при процессе:
Изобарном 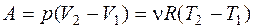 ,
,
Изотермическом 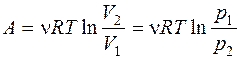 ,
,
адиабатном
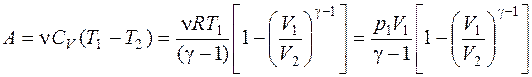 ,
,
где 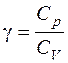 .
.
Уравнение Пуассона (уравнение адиабатного процесса)
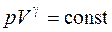 ,
, 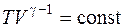 ,
, 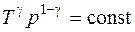 .
.
Коэффициент полезного действия цикла Карно
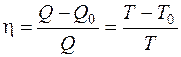 ,
,
где
Q и T – количество теплоты, полученное от нагревателя, и его температура,
Q0 и T0 – количество теплоты, переданное холодильнику, и его температура.
Изменение энтропии при переходе из состояния 1 в состояние 2
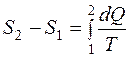
Уравнение Ван - дер - Ваальса:
для 1 моль газа 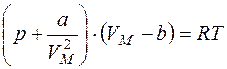 ,
,
для ν моль газа 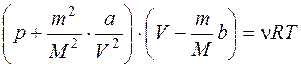 ,
,
где a и b – постоянные Ван - дер - Ваальса,
VM – объем 1 литра газа.
Критические параметры 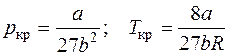 .
.
Собственный объем молекулы 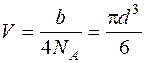 .
.
Высота поднятия жидкости в капилляре радиусом r
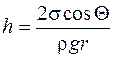 .
.
Примеры решения задач
Молекулярно-кинетическая теория идеальных газов
Задача 1. Определить, сколько киломолей и молекул водорода содержится в объеме 50 м3 под давлением 767 мм рт. ст. при температуре 18°С. Какова плотность и удельный объем газа?
| Дано: V = 50 м3 Ρ = 767 мм. рт. ст. @ 767·133 Па Т = 291 К М = 2 кг/моль | Решение:
На основании уравнения Менделеева – Клайперона:
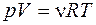 устанавливаем число киломолей ν, содержащихся в заданном объеме V. Зная р - давление, V – объем, Т – температуру газа, R – молярную газовую постоянную устанавливаем число киломолей ν, содержащихся в заданном объеме V. Зная р - давление, V – объем, Т – температуру газа, R – молярную газовую постоянную
|
| ν – ? N – ? ρ – ? d – ? |
можно определить ν:
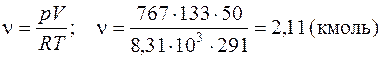
Число молекул N, содержащихся в данном объеме, находим, используя число Авогадро NА (которое определяет какое количество молекул содержится в одном киломоле). Общее количество молекул, находящихся в массе m данного газа, может быть установлено, так как известно число молей ν.
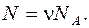
Подставляя в формулу число киломолей, устанавливаем число молекул, содержащихся в объеме V: 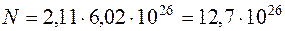 .
.
Плотность газа ρ = m/V определяем из уравнения Менделеева - Клайперона:
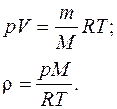
Подставляя числовые значения в единицах СИ в формулу, определим плотность газа:
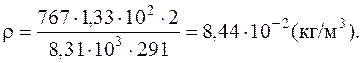
Удельный объем газа d определяем из уравнения Менделеева - Клайперона:
|
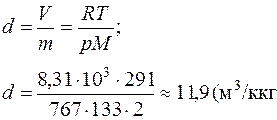
Ответ: 11,9 м3/кг.
Задача 2. В сосуде объемом 2 м3 находится смесь 4 кг гелия и 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
| Дано: V = 2 м3 m1= 4 кг М1= 4·10-3 кг/кмоль m2= 2 кг М2= 2·10-3 кг/кмоль Т1= 300 К | Решение:
Воспользуемся уравнением Менделеева - Клайперона, применив его к гелию и водороду:
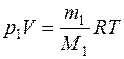 (1) (1)
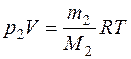 (2)
где р1 – парциальное давление гелия; m1– масса гелия; (2)
где р1 – парциальное давление гелия; m1– масса гелия;
|
| р - ? М - ? |
М1 – егомолярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль·К) –молярная газовая постоянная; р2– парциальное давление водорода; m2– масса водорода; М2 – его молярная масса.
По закону Дальтона: 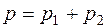 (3)
(3)
Из уравнений (1) и (2) выразим р1и р2и подставим в уравнение (3):
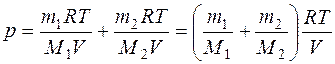 (4)
(4)
С другой стороны, уравнение Менделеева - Клайперона для смеси газов имеет вид:
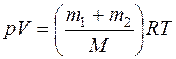 (5)
(5)
Сравнивая (4) и (5) найдем молярную массу смеси газов по формуле:
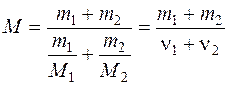 , (6)
, (6)
где ν1 и ν2 – число молей гелия и водорода соответственно.
|
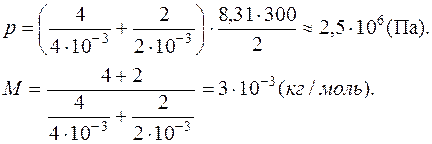
Ответ: 3·10-3 кг/моль.
Задача 3. При каком давлении средняя длина свободного пробега молекул водорода <λ> = 2,5 см при температуре 68°С? Диаметр молекул водорода принять равным d = 2,3·10 –10 м.
| Дано: <λ>= 2,5·10-2 м Т= 341 К d= 2,3·10-10 м NA = 6,02·1026 кмоль-1 | Решение: Давление водорода при температуре Т можно найти по уравнению Менделеева- Клайперона, в котором удобно ввести число молекул n0 в 1 м3. |
| р – ? |
Это проводится следующим образом:
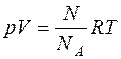 ;
; 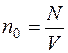 ;
; 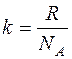 ;
;
где NA – число Авогадро и k – постоянная Больцмана.
Следовательно, 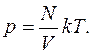 Так как
Так как 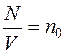 , имеем
, имеем 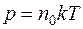 .
.
Число молекул в 1 м3 выразим через среднюю длину свободного пробега. Из формулы 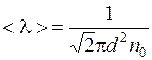 , находим
, находим 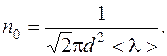 Таким образом:
Таким образом:
|
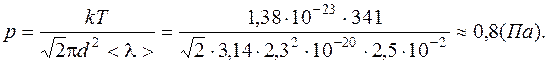
Ответ: 0,8 Па.
Задача 4. Определить плотность разреженного азота, если средняя длина свободного пробега молекул 10 см. Какова концентрация молекул?
| Дано: < λ > = 10 см = 0,1 м | Решение: Средняя длина пробега молекулы определяется формулой: |
| р - ? n0 - ? |
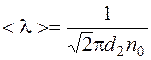 , (1)
, (1)
где d – эффективный диаметр молекул (для азота d = 0,31·10 –9 м).
Концентрацию молекул найдем из равенства:
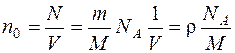 , (2)
, (2)
где NA – число Авогадро; М = 28·10 –3 кг/моль – молярная масса азота.
Решая совместно уравнения (1) и (2), находим: 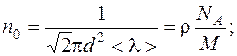
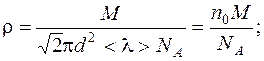
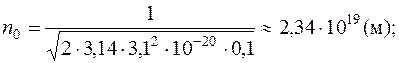
|
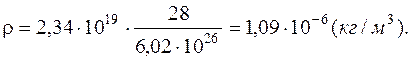
Ответ: 1,09·10-6 кг/м3.
Задача 5. Вычислить коэффициент внутреннего трения и коэффициент диффузии кислорода, находящегося при давлении 0,2 МПа и температуре 280 К.
| Дано: p = 2·105 Па d = 2,9·10-10 м М = 32·10-3 кг/моль Т = 280 К | Решение: На основании представлений молекулярно – кинетической теории газов коэффициент внутреннего трения идеального газа (динамическая вязкость) и коэффициент диффузии определяются по формулам: |
| η - ? D - ? |
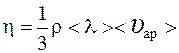 (1);
(1); 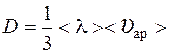 (2),
(2),
где ρ– плотность газа; < λ > – средняя длина свободного пробега молекул; <υар> – средняя арифметическая скорость молекул.
Из (1) и (2) следует 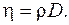 (3)
(3)
Среднюю арифметическую скорость и среднюю длину свободного пробега молекул находим по формулам:
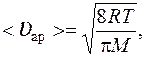 (4)
(4) 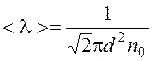 , (5)
, (5)
где R = 8,31 Дж/(моль·К) – молярная газовая постоянная; Т – термодинамическая температура; d = 2,9·10 –10 м – эффективный диаметр молекулы кислорода; n0 – число молекул в 1 м3 (концентрация).
Из уравнения Менделеева - Клайперона определяем n0
(см. задачу 3): 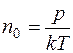 (6)
(6)
где р – давление; k = 1,38·10 –23 Дж/К – постоянная Больцмана.
Подставляя (6) в уравнение (5), получаем: 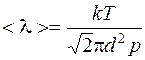 . (7)
. (7)
Окончательный вид расчетной формулы для коэффициента диффузии найдем, подставляя выражения (4) и (7) в уравнение (2):
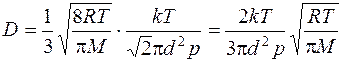 . (8)
. (8)
Плотность кислорода определяется по формуле: 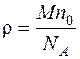 . С учетом (6) имеем:
. С учетом (6) имеем: 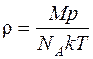 . (9)
. (9)
Подставляя (9) и (8) в (3), получаем расчетную формулу для коэффициента внутреннего трения: 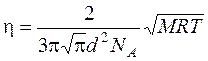 .
.
Вычисляем: 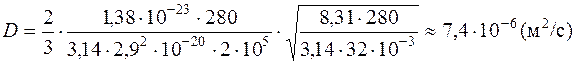
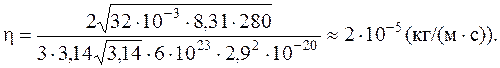
Ответ: 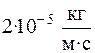 .
.
Задача 6. Наружная поверхность кирпичной стены площадью 25 м2 и толщиной 37 см имеет температуру 259 К, а внутренняя поверхность–293 К. Помещение отапливается электроплитой. Определить ее мощность, если температура в помещении поддерживается постоянной. Теплопроводность кирпича 0,4 Вт/(м·К).
| Дано: S = 25 м2 D = 37 см = 0,37 м T1 = 259 K T2 = 293R χ = 0,4 Вт/(м·К) | Решение:
Количество теплоты, прошедшее через наружную стену, определим по закону Фурье:
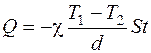 (1)
где t – время протекания теплоты. (1)
где t – время протекания теплоты.
|
| N - ? |
За время t – электроплита должна выделить такое же количество теплоты: 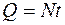 (2)
(2)
Приравнивая правые части уравнений (1) и (2), получаем:
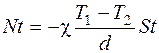 ,
,
откуда 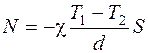 ,
, 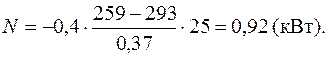
Ответ: 0,92 кВт.
2. Основы термодинамики
Задача 7. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К.
| Дано: т = 2 кг Т = 400 К М = 2·10 –3 кг/моль | Решение: Считаем водород идеальным газом. Молекула водорода – двухатомная. Связь между атомами считаем жесткой, тогда |
| <Eпост> - ? <Eвр> - ? |
число степенейсвободы молекулы водорода равно 5. В среднем на одну степень свободы приходится энергия: 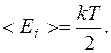 Поступательному движению приписывается три (i = 3), а вращательному две (i= 2) степени свободы. Тогда энергия одной молекулы:
Поступательному движению приписывается три (i = 3), а вращательному две (i= 2) степени свободы. Тогда энергия одной молекулы:
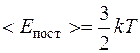 ,
, 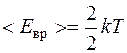 .
.
Число молекул, содержащихся в массе газа m: 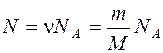 , где ν – число молей, NA – число Авогадро. Тогда средняя кинетическая энергия поступательного движения молекул водорода будет:
, где ν – число молей, NA – число Авогадро. Тогда средняя кинетическая энергия поступательного движения молекул водорода будет: 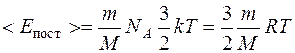 , (1)
, (1)
где R = kNA – молярная газовая постоянная.
Средняя кинетическая энергия вращательного движения молекул водорода: 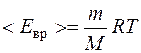 . (2)
. (2)
Подставляя числовые значения и формулы (1) и (2), имеем:
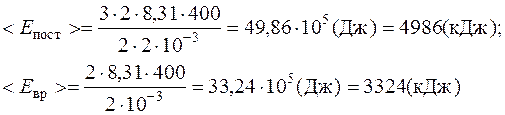
Ответ: 4986 кДж, 3324 кДж.
Задача 8. При адиабатическом сжатии давление воздуха было увеличено от Р1 = 100 кПа до Р2 = 1 МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление Р3 газа в конце процесса.
 Дано:
Р1 =100 кПа=1·105 Па
Р2 = 1 МПа =1·106 Па
V2 = const
g = 1,4
Р3 – ? Дано:
Р1 =100 кПа=1·105 Па
Р2 = 1 МПа =1·106 Па
V2 = const
g = 1,4
Р3 – ?
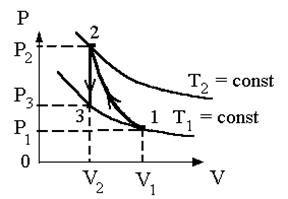
| Решение:
На PV диаграмме представлен график, соответствующий процессу, указанному в условии задачи.
|
Процесс адиабатического сжатия 1-2 совершается без теплообмена и согласно уравнению Пуассона:
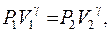
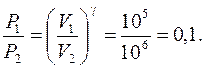 (1)
(1)
Макроскопические параметры P, V, T воздуха в состоянии 1, 2, 3 связаны соотношением:
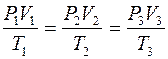 ,
,
откуда P1V1 = P3V3.
По условию задачи V2 = V3.Используя уравнение (1) можно записать
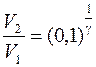 .
.
Тогда 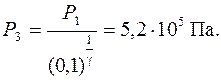
Ответ: 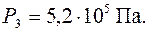
Задача 9. Вычислить массу столба воздуха высотой 1 км и сечением 1 м2, если плотность воздуха у поверхности Земли 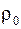
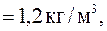 а давление Р0 = 1,013 ∙ 105 Па. Температуру воздуха считать одинаковой.
а давление Р0 = 1,013 ∙ 105 Па. Температуру воздуха считать одинаковой.
Дано:
h = 1 км = 1000 м
S = 1 м2
Т = const
Р0=1,013 ∙ 105 Па
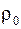 = 1,2 кг/м 3 = 1,2 кг/м 3
| Решение:
Атмосферное давление меняется с высотой, плотность воздуха также является функцией высоты 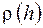 . Массу воздуха в элементе объема dV представим в виде:
dm = . Массу воздуха в элементе объема dV представим в виде:
dm = 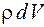 .
Найдем изменение плотности воздуха с высотой. .
Найдем изменение плотности воздуха с высотой.
|
| m – ? | Согласно уравнению состояния идеального газа |
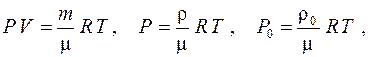
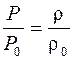 . (1)
. (1)
Продифференцировав (1), получим 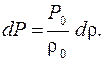 (2)
(2)
С другой стороны убыль давления dP при переходе от высоты h0 к высоте h0 + dh
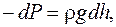 (3)
(3)
где 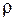 – плотность воздуха на высоте h.
– плотность воздуха на высоте h.
Используя уравнения (2) и (3) получим:
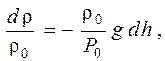
или
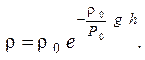
Вычислим массу столба воздуха
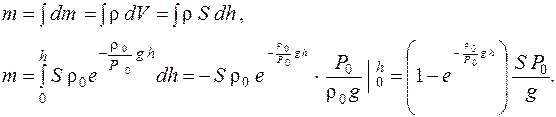
Подставив данные, приведенные в условии задачи получим:
m = 1,13 · 103 кг.
Ответ: m = 1,13 · 103 кг.
Задача 10. Определить скорость вылета поршня массой 4 кг из цилиндра при адиабатном расширении кислорода в 40 раз, если начальное давление воздуха 107 Па, а объем 0,3 л.
| Дано: Т = 4 кг V2/V1 = 40 p1 = 10 7Па V1 = 0,3 л = 3·10-4 м3 | Решение: Работа А, совершаемая адиабатически расширяющимся воздухом, в данном случае идет на увеличение кинетической энергии поршня, т. е |
| υ - ? |
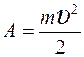 ,
,
где т и υ – масса и скорость поршня.
Для подсчета работы адиабатически расширяющегося газа воспользуемся формулой: 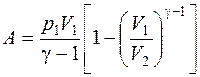 , где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме (для кислорода γ =1,4).
, где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме (для кислорода γ =1,4).
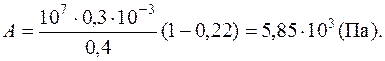 Так как
Так как 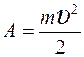 , то
, то 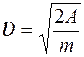 ,
, 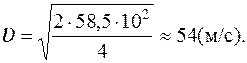
Ответ: 54 м/с.
Задача 11. Молекулярный пучок кислорода ударяется о неподвижную стенку. После соударения молекулы отражаются от стенки с той же по модулю скоростью. Определить давление пучка на стенку, если скорость молекул 500 м/с и концентрация молекул в пучке 5·10 24 м -3.
| Дано: υ = 500 м/с n0= 5·10 24 м –3 | Решение:
Давление определяется по формуле: 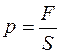 , (1) , (1)
|
| р - ? |
где F – сила давления, S – площадь.
Силу давления найдем из второго закона Ньютона:
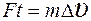 , (2)
, (2)
где m – масса кислорода, ударившегося о стенку за время t, Δυ – изменение скорости молекул при ударе.
Массу одной молекулы кислорода найдем из закона Авогадро: 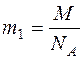 , где М = 32·1023 кг/моль – молярная масса кислорода; NA =
, где М = 32·1023 кг/моль – молярная масса кислорода; NA = 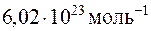 – постоянная Авогадро.
– постоянная Авогадро.
За время t о стенку ударяются молекулы, находящиеся в объеме: 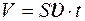 , масса которых:
, масса которых: 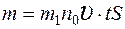 . (3)
. (3)
Изменение скорости при соударении: 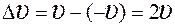 . (4)
. (4)
Подставляя выражения (3), (4) в (2), находим: 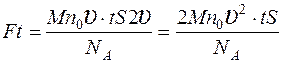 , откуда
, откуда 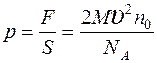 ,
, 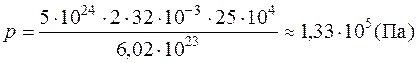 .
.
Ответ: 1,33·105 Па.
Задача 12. Определить удельные теплоемкости ср, сv, для смеси 1 кг азота и 1 кг гелия.
| Дано: m1= 1 кг М1= 28 кг/кмоль i1 = 5 m2 = 1 кг М2= 4 кг/кмоль газа. i2 = 3 | Решение: Удельной теплоемкостью какого – либо газа называется величина, равная количеству теплоты, которое нужно сообщить единице массы тела, чтобы повысить его температуру на 1 градус. При этом величина теплоемкости зависит от условий, при которых |
| ср - ? сv - ? |
происходит нагревание. Если нагревание происходит при постоянном объеме, то: 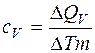 , где
, где 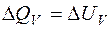 , т.е. все сообщаемое количество теплоты идет на изменение внутренней энергии системы. Изменение внутренней энергии смеси газа определяется формулой:
, т.е. все сообщаемое количество теплоты идет на изменение внутренней энергии системы. Изменение внутренней энергии смеси газа определяется формулой: 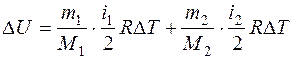 , где i1 и i2 – число степеней свободы первого и второго газов.
, где i1 и i2 – число степеней свободы первого и второго газов.
Окончательно получим: 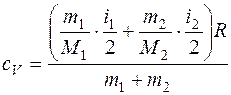 . (1)
. (1)
Если нагревание происходит при постоянном давлении, то
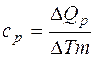 , (2)
, (2)
где 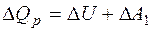 , т.е. сообщаемое газу количество теплоты идет не только на изменение внутренней энергии, но и на работу по расширению газа. Работа при изобарическом расширении для каждого газа равна:
, т.е. сообщаемое газу количество теплоты идет не только на изменение внутренней энергии, но и на работу по расширению газа. Работа при изобарическом расширении для каждого газа равна: 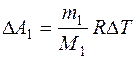 ;
; 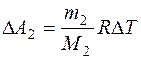 , поэтому:
, поэтому:
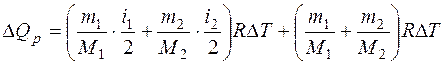 .
.
Подставляя это значение в уравнение (2), получим:
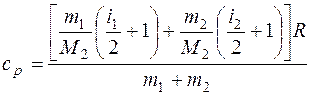 .
.
Произведем вычисления:
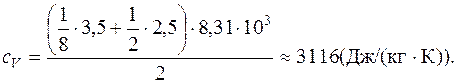
Ответ: 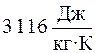 .
.
Задача 13. В цилиндре под поршнем находится водород, который имеет массу 0,02 кг и начальную температуру 27°С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и работу, совершаемую газом. Изобразить процесс графически.
Дано:
m = 0,02 кг
Т1 = 27°С = 300 К
М = 2 кг/кмоль
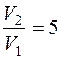 i = 5
i = 5
| Решение:
При адиабатном процессе температура и объем газа связаны
соотношением: 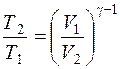 , где , где 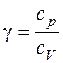 – отношение теплоемкостей газа при – отношение теплоемкостей газа при
|
| T2 - ? А - ? |
постоянном давлении и постоянном объеме. Для водорода γ = 1,4.
Отсюда выражение для конечной температуры Т2 будет:
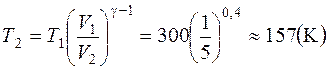 .
.
Работа А1 газа при адиабатическом расширении равна изменению внутренней энергии:
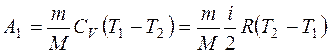 .
.
|
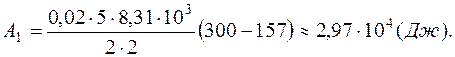
Работа А2 газа при изотермическом процессе может быть выражена в виде: 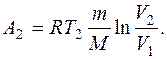
|
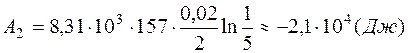 .
.
Знак «минус» показывает, что при сжатии газа работа совершается над газом внешними силами. Полная работа, совершенная газом при описанных процессах, равна:
|
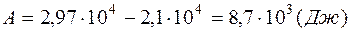 .
.
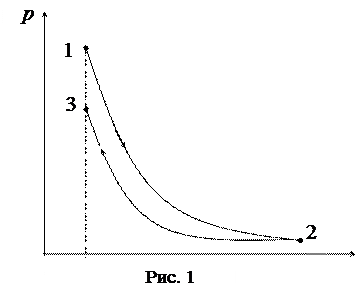
График процесса приведен на рисунке 1.
 |
Ответ: 8,7 · 103 Дж.
Задача 14. Кислород массой m = 2 кг занимает объем V1= 1 м3 и находится под давлением р1= 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2= 3 м3, а затем при постоянном объеме до давления р3= 0,5 МПа. Найти изменение ΔU внутренней энергии газа, совершенную им работу А и количество теплоты Q, переданное газу. Построить график процесса.
| Дано: m = 2 кг М = 32 кг/моль V1= 1 м3 р1 = р2 = 2·105 Мпа V2= 3 м3 р3 = 5·105 Мпа R = 8,31·10 –3 Дж/(кмоль·К) | Решение:
Изменение внутренней энергии газа выражается формулой:
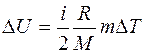 , (1)
где i – число степеней свободы молекул газа для двухатомных молекул кислорода (i = 5); М – молярная масса; R – молярная газовая постоянная. , (1)
где i – число степеней свободы молекул газа для двухатомных молекул кислорода (i = 5); М – молярная масса; R – молярная газовая постоянная.
|
| ΔU - ? А - ? Q - ? |
Начальную и конечную температуры найдем, используя уравнение Менделеева - Клайперона:
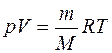 . (2)
. (2)
Решая его относительно Т, получим: 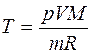 (3)
(3)
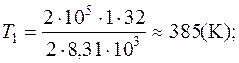
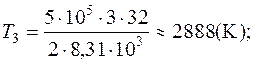
Подставляя в выражение (1) числовые значения входящих в него
величин, находим: 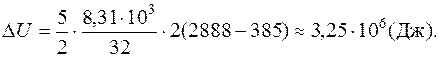
Работа расширения газа при постоянномдавлении выражается формулой: 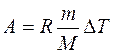 . Подставив числовые значения, получим:
. Подставив числовые значения, получим:
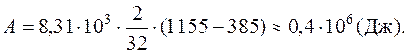
Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. А2 = 0. Следовательно, полная работа, совершенная газом, равна: 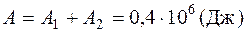 . Согласно первому началу термодинамики количество теплоты Q, переданное газу, равно сумме изменения внутренней энергии ΔU и работы А:
. Согласно первому началу термодинамики количество теплоты Q, переданное газу, равно сумме изменения внутренней энергии ΔU и работы А: 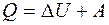 , следовательно:
, следовательно: 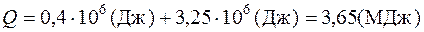 .
.
График процесса приведен на рисунке 2.
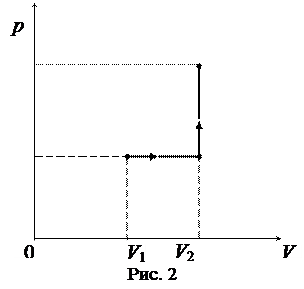 |
Ответ: 3,65 МДж.
Задача 15. Идеальный двухатомный газ, содержащий количество вещества n = 1 моль и находящийся под давлением Р1 = 0,1 МПа при температуре Т1 = 300 К, нагревают при постоянном объеме до давления Р2 = 0,2 МПа. После этого газ изотермически расширялся до начального давления и затем изобарно был сжат до начального объема V1. Построить график цикла. Определить температуру Т газа для характерных точек цикла и его термический КПД h.
Дано:
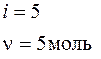 Р1= 0,1 Мпа = 1·105 Па
Т1= 300 К
Р2= 0,2 Мпа = 2·105 Па
Р1= 0,1 Мпа = 1·105 Па
Т1= 300 К
Р2= 0,2 Мпа = 2·105 Па
| Решение:
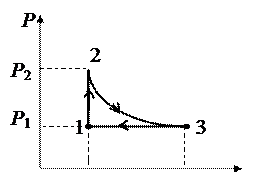 В координатах Р, V график цикла имеет следующий вид В координатах Р, V график цикла имеет следующий вид

|
| T2 – ? Т3 – ? h – ? |
V1 V2 V 
|
Переход газа на участке 1-2 происходит изохорически при V1 = const. Давления и температуры газов в состояниях 1 и 2 связаны между собой соотношением:
 =
= 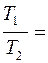
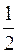 .
. 
Отсюда T2 = 2Т1 = 600 K.
Так как переход газа 2-3 изотермический, то Т2 = Т3.
Термический КПД цикла определяется выражением 
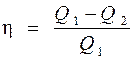 , (1)
, (1)
где Q1 – количество теплоты, полученное от нагревателя за цикл, Q2 – количество теплоты, отданное холодильнику за цикл.
Газ получает количество теплоты на участках 1-2 и 2-3
Q 1= Q 1-2 + Q 2-3,
где Q 1-2 = C v v (T 2 - T 1) – количество теплоты, полученное при изохорическом нагревании,
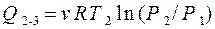 – количество теплоты, полученное при изотермическом расширении.
– количество теплоты, полученное при изотермическом расширении.
Газ отдает количество теплоты на участке 3-1 при изобарическом сжатии:
Q 3-1 = Q 2 = Cр 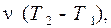

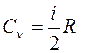 – молярная теплоемкость газа при V = const, C р
– молярная теплоемкость газа при V = const, C р 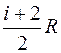 – молярная теплоемкость газа при P = const.
– молярная теплоемкость газа при P = const. 
Подставив значения Q 1 и Q 2, С v и С р  в формулу (1) получим:
в формулу (1) получим:
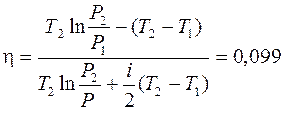 ,
, 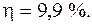
Ответ: T 2 = T 3 = 600 K, η = 9,9 %.
Задача16. Кислород массой 1 кг совершает цикл Карно. При изотермическом расширении газа его объём увеличивается в 2 раза, а при последующем адиабатическом расширении совершается работа 3000 Дж. Определить работу, совершенную за цикл.
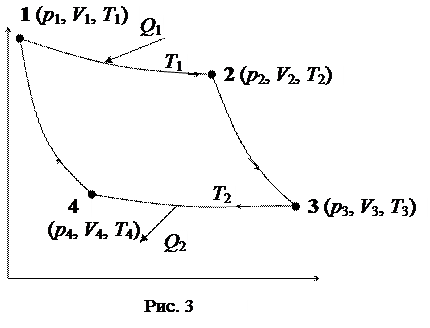
| Дано: V2 = 2V1 A2-3 = 3000 Дж i = 5 | Решение: Идеальный цикл Карно состоит из двух изотерм и двух адиабат (рис. 3). |
| А - ? |
На рисунке 3 участок 1-2 соответствует изотермическому расширению газа (Т1 = Т2), участок 2-3 – адиабатическому расширению газа, участок 3-4 – изотермическому сжатию (Т3 = Т4) и участок 4-1 – адиабатическому сжатию.
При изотермическом расширении внутренняя энергия идеального газа остается постоянной, следовательно, все подводимое тепло Q1 идет на работу по расширению газа на участке 1-2, т.е.
 |
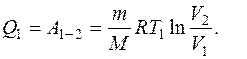 (1)
(1)
При изотермическом сжатии на участке 3-4 Q2 тепло отдается холодиль
|
из
5.00
|
Обсуждение в статье: Молекулярно-кинетическая теория идеальных газов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

