Классический метод расчета переходных процессов

Министерство образования и науки РФ

ФГБОУ ВПО «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра электротехники и электрических машин

 

 

УТВЕРЖДАЮ

 

И.о. зав. кафедрой ЭТиЭМ

 

к.т.н., доцент

Я.М. Кашин

___ августа 2013 г.

 

 

Лекция № 10

По дисциплине «Электротехника»

для студентов направления подготовки: 131000 - «Нефтегазовое дело»

Квалификация выпускника - Бакалавр

 

Тема 5. Переходные процессы в линейных электрических цепях

 

Разработал:

доц.каф.ЭТиЭМ Копелевич Л.Е.

доц.каф.ЭТиЭМ Квон А.М.

 

Обсуждено на заседании каф. ЭТиЭМ

27 августа 2013 г. (протокол № 1)

Секретарь кафедры

доц. С.А. Попов

 

 

2013 г.

Цели: 1. Формирование следующих компетенций:

1. ОК-9: способности к целенаправленному применению базовых знаний в области математических, естественных, гуманитарных и экономических наук в профессиональной деятельности.

2. Формирование уровня обученности:

1. Знать: основные законы электротехники.

Материальное обеспечение:

Проектор, ПК, комплект слайдов «ЭиЭ, тема 5».

Учебные вопросы

Вводная часть.

Основная часть:

1. Основные понятия и принципы анализа переходных процессов.

2. Законы коммутации.

3. Классический метод расчета переходных процессов.

4. Переходный процесс при подключении катушки индуктивности в цепи с источником постоянной ЭДС.

5. Переходные процессы заряда и разряда емкостного элемента в цепи с источником постоянной ЭДС.

Заключение.

Литература

1. Касаткин А.С. Курс электротехники: Учеб. для вузов/ А.С. Касаткин, М.В. Немцов. ­- 10-е изд., стер. - М.: Высш. школа, 2009. – 542 с. (с. 132 - 158).

Основные понятия и принципы анализа переходных процессов.

Определение переходных процессов.

Под переходными про­цессами понимают процессы перехода от одного режима работы электрической цепи (обычно периодического) к другому (обычно также периодическому), чем-либо отличающемуся от предыдуще­го, например амплитудой, фазой, формой или частотой, действую­щей в схеме ЭДС, значениями параметров схемы, а также вследст­вие изменения конфигурации цепи.

Периодическими являются режимы синусоидального и посто­янного тока, а также режим отсутствия тока в ветвях цепи.

Переходные процессы вызываются коммутацией в цепи. Ком­мутация — это процесс замыкания (рис. 1, а) или размыкания (рис. 1, б) выключателей.

Физически переходные процессы представляют собой процессы перехода от энергетического состояния, соответствующего докоммутационному режиму, к энергетическому состоянию, соответству­ющему послекоммутационному режиму.

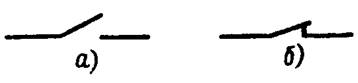
Рис. 1

 

Переходные процессы обычно являются быстро протекающи­ми; длительность их составляет десятые, сотые, а иногда даже мил­лиардные доли секунды; сравнительно редко длительность пере­ходных процессов достигает секунд и десятков секунд. Тем не менее, изучение переходных процессов важно, так как оно дает возмож­ность установить, как деформируются по форме и амплитуде сиг­налы при прохождении их через усилители и другие устройства, позволяет выявить превышения напряжения на отдельных участ­ках цепи, которые могут оказаться опасными для изоляции уста­новки, увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока установившегося периодического про­цесса (и вызвать недопустимые механические усилия), а также оп­ределить продолжительность переходного процесса.

Приведение задачи о переходном процессе к решению линейного дифференциального уравнения с постоянными коэффи­циентами. Запишем уравнение по второму закону Кирхгофа для схемы рис. 2 при замкнутом ключе. Сумма падений напряжений на элементах L и R равна ЭДС Е:

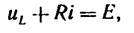
или

 

Рис. 2

 

Как известно из курса математики, уравнение, содержащее не­известную функцию (в нашем случае i) и ее производные (в нашем случае Ldi/dt), называют дифференциальным уравнением.

Таким образом, определение тока как функции времени, по сути дела, есть решение дифференциального уравнения.

Известно, что решение дифференциального уравнения — это отыскание функции, удовлетворяющей ему. Подстановка этой фун­кции и ее производных превращает дифференциальное уравнение в тождество.

Решение линейных дифференциальных уравнений будем прово­дить в основном четырьмя методами: классическим, операторным, методом интеграла Дюамеля и методом пространства состояний.

 

Законы коммутации.

Обоснование невозможности скачка тока через индуктив­ную катушку и скачка напряжения на конденсаторе.

Доказатель­ство того, что ток через индуктивную катушку не может изменяться скачком, проведем на примере схемы рис.2. По второму закону Кирхгофа

(1)

Ток i и ЭДС Е могут принимать конечные (не бесконечно боль­шие) значения.

Допустим, что ток i может измениться скачком. Скачок тока означает, что за бесконечно малый интервал времени Dt®0 ток изменится на конечное значение Di. При этом Di/Dt®¥. Если вме­сто Ldi/dt в уравнение (1) подставить ¥, то его левая часть не будет равна правой части и не будет выполнен второй закон Кирхгофа.

Следовательно, допущение о возможности скачкообразного из­менения тока через индуктивную катушку противоречит второму закону Кирхгофа.

Ток через L не может изменяться скачком, но напряжение на L, равное Ldi/dt, скачком измениться может. Это не противоречит второму закону Кирхгофа.

Доказательство того, что напряжение на конденсаторе не может изменяться скачком, проводится аналогично.

Обратимся к простейшей цепи с конденсатором (рис. 3, a). Составим для нее уравнение по второму закону Кирхгофа:

где Е — ЭДС источника, конечная величина; u_C — напряжение на конденсаторе.

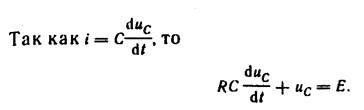(2)

Рис. 3

Если допустить, что напряжение u_C может измениться скачком, то Du_C/Dt » du_C/dt®¥ и левая часть (2) не будет равна правой части. Отсюда следует, что допущение о возможности скачкообразного изменения напряжения на конденсаторе противоречит второму закону Кирхгофа. Однако ток через конденсатор, равный Cdu_C/dt, может изменяться скачком; это не противоречит второму закону Кирхгофа.

Из указанных двух основных положений следуют два закона (правила) коммутации.

Первый закон (правило) коммутации. Ток через индуктив­ный элемент L непосредственно до коммутации L(0_-) равен току через этот же индуктивный элемент непосредственно после комму­тации L(0₊):

(3)

Время t=0_- представляет собой время непосредственно до коммутации, t=0₊ — после коммутации (рис. 3, б). Равенство (3) выражает собой первый закон коммутации.

Второй закон (правило) коммутации. Обозначим напря­жение на конденсаторе непосредственно до коммутации u_C(0_-), а напряжение на нем непосредственно после коммутации u_C(0₊).

В соответствии с невозможностью скачка напряжения на кон­денсаторе

(4)

Равенство (4) выражает собой второй закон коммутации.

 

 

Классический метод расчета переходных процессов.

 

Общая характеристика методов анализа переходных процессов в линейных электрических цепях.

Расчет переходных про­цессов в любой линейной электрической цепи состоит из следующих основных операций:

1) выбора положительных направлений токов в ветвях цепи;

2) определения значений токов и напряжений непосредственно до коммутации;

3) составления характеристического уравнения и нахождения его корней;

4) получения выражения для искомых токов и напряжений как функции времени.

Широко распространенными методами расчета переходных процессов являются:

1) метод, называемый в литературе классическим;

2)операторный метод;

3) метод расчета с помощью интеграла Дюамеля. Для всех этих методов перечисленные операции (этапы расчета) являются обязательными. Для всех методов первые три операции

совершают одинаково и их нужно рассматривать как общую для всех методов часть расчета. Различие между методами имеет место на четвертом, наиболее трудоемком этапе расчета.

Чаще используют классический и операторный методы, реже — метод расчета с применением интеграла Дюамеля. В дальнейшем будут даны сравнительная оценка и рекомендуемая область при­менения каждого из них.

В радиотехнике, вычислительной и импульсной технике, элект­ронике, автоматике и в технике, связанной с теорией информации, кроме этих трех методов применяют метод анализа переходных процессов, основывающийся на интеграле Фурье. Для исследования характера переходного процес­са, описываемого уравнениями высоких порядков, используют мо­делирующие установки, а также метод пространства состояний.

Классический метод расчета переходных процессов.

Классическим методом расчета переходных процессов называют метод, в котором решение дифференциального уравне­ния представляет собой сумму принужденной и свободной состав­ляющих. Определение постоянных интегрирования, входящих в вы­ражение для свободного тока (напряжения), производят путем совместного решения системы линейных алгебраических уравне­ний по известным значениям корней характеристического уравне­ния, а также по известным значениям свободной составляющей тока (напряжения) и ее производных, взятых при t=0₊.

Определение постоянных интегрирования в классическом методе. Как известно из предыдущего, любой свободный ток (на­пряжение) можно представить в виде суммы экспоненциальных слагаемых. Число членов суммы равно числу корнем характеристи­ческого уравнения.

При двух действительных неравных корнях

при трех действительных неравных корнях

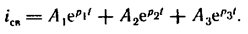
Для любой схемы с помощью уравнений Кирхгофа и законов ком­мутации можно найти:

1) числовое значение искомого свободного тока при t=0₊, обозначим его i_св(0₊);

2) числовое значение первой, а если понадобится, то и высших производных от свободного тока, взятых при t=0₊. Числовое значение первой производной от свободного тока при t=0₊ обозначим i_св^’(0₊); второй — i_св^¢(0₊) и т.д.

Рассмотрим методику определения постоянных интегрирования А₁, А₂,..., полагая известными i_св(0₊), i_св^¢(0₊), i_св^¢¢(0₊) и значения корней p₁, p₂, … .

Если характеристическое уравнение цепи представляет собой уравнение первой степени, то i_св=Ae^pt_. Постоянную интегрирова­ния А определяют по значению свободного тока i_св(0₊):

Если дано характеристическое уравнение второй степени и его корни действительны и не равны, то

(5)

Продифференцируем это уравнение по времени:

(5a)

Запишем уравнения (5) и (5а) при t = 0 (учтем, что при t = 0 e^p1t = e^p2t = 1). В результате получим

(6)

(6а)

В этой системе уравнений известными являются i_св(0₊), i_св^¢(0₊), p₁ и p₂; неизвестными — А₁ и А₂.