Теплопроводность в стержне (ребре) постоянного поперечного сечения

 

а) Дифференциальное уравнение и его решение

Ребра в поперечном сечении могут иметь профиль самой различной геометрической конфигурации (прямоугольник, круг, треугольник и другие фигуры, в том числе и неправильной геометрической формы). Рассмотрим рас­пространение тепла в прямом стержне с по­стоянным по длине поперечным сечением. Обозначим площадь поперечного сечения стержня через f и периметр через и. Стер­жень находится в среде с постоянной тем­пературой tж, коэффициент теплоотдачи от поверхности стержня к окружающей среде будем считать постоянным для всей поверх­ности. Будем полагать также, что коэффи­циент теплопроводности материала стерж­ня λ достаточно велик, а поперечное сече­ние очень мало по сравнению с его длиной. Последнее дает основание пренебречь изме­нением температуры в поперечном сечении и считать, что она изменяется только вдоль оси стержня. Для удобства дальнейших выкладок отсчет температуры будем вести от t_ж=const. Отсчитанную таким образом избыточную тем­пературу стержня обозначим через υ. Очевидно, если задана температура основания стержня t1, , то избыточная температура основания стержня (рис. 2.3) будет: υ₁ =t₁—t_ж.

	t     υ1 d υ t1 υ     tж x   x dx   Qx Qx+dx     dQ

 

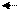Рис. 2.3. Теплопередача через стержень.

где t_ж — температура среды, окружающей стержень;

t — текущая температура стержня.

 

На расстоянии х от основания стержня выделим элемент стержня длиной dx. Уравнение теплового баланса для рассматриваемого эле­мента стержня можно записать:

Q_x—Q_x+dx = dQ, (a)

. где Qx — количество тепла, входящее в левую грань элемента за еди­ницу времени;

Qx+dx — количество тепла, которое выходит из противоположной грани элемента за то же время;

dQ —количество тепла, отдаваемого за единицу времени наружной

поверхностью элемента окружающей его среде. Согласно закону Фурье

и

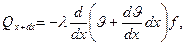
откуда

.

Следовательно,

С другой стороны, согласно закону Ньютона—Рихмана

(в)

Приравнивая (б) и (в), получим следующее дифференциальное уравнение, описывающее изменение температуры стержня:

(2.22)

где

(г)

Из выражения (г) видно, что для заданного ребра при условии постоянства коэффициента теплоотдачи α_р по всей поверхности и по­стоянства λ в рассматриваемом интервале температур величина m=const. Тогда общий интеграл для уравнения (2.22) будет:

(2.23)

Значения постоянных С₁ и С₂ определяются из граничных условий. Граничные условия могут быть заданы по-разному в зависимости от длины стержня и других факторов.

б) Стержень бесконечной длины

В начальном сечении стержня температура поддерживается посто-
янной, т. е. при х=0 = 1. Если длина стержня l=∞, то все тепло, подводимое к стержню, будет отдано им в окружающую среду и при х= ∞ =0.

Подстановка граничных условий в уравнение (2.23) дает:

при х=0 ₁ = C₁+C₂;

при х = ∞ C₁e ^∞ =Q.

Последнее равенство возможно только при C₁ = 0. Таким образом C₂= ₁. Подставляя значения постоянных C₁ и С₂ в уравнение (2.23), получаем

l

= 1е-^{mx o}C (2.24)

m1

x

m3

m2

Рис. 2.4. Изменение температуры по длине стержня.

 

Последнее равенство можно записать в следующем виде

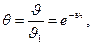(2.25)

 

где θ — безразмерная температура, выраженная в долях температу­ры 1 начального сечения стержня.

На рис. 2.4 представлена зависимость безразмерной температуры θ от длины стержня при различных значениях параметра m(m1 <m2<m3).

Из рассмотрения рис. 2.4 следует, что безразмерная температура убывает тем сильнее, чем больше множитель m. При х → ∞ все кривые асимптотически приближаются к θ = 0.

Из уравнения следует, что m пропорционально теплоотдаче с боковой поверхности и обратно пропорционально —фактору, определяющему передачу тепла теплопроводностью вдоль стержня. Отсюда следует, что при оребрении нужно выбирать материал для ребер с большим коэффициентом теплопроводности. Последнее приводит к умень­шению m и сохранению больших избыточных температур вдоль стержня.

При = const m возрастает с возрастанием , что указывает на более эффективную работу ребер с профилями, имеющими меньшее отношение при том же поперечном сечении.

Количество тепла, передаваемого стержнем в окружающую среду, очевидно будет равняться количеству тепла, проходящему через его осно­вание.

Через основание стержня проходит тепловой поток

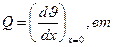
Из уравнения (2.24) находим:

Подставляя значение градиента температуры при х = 0 в предыдущее уравнение для теплового «потока, получим формулу, определяющую количество тепла (тепловой поток), отданного (или воспринятого) стержнем в окружающую среду:

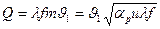(2.26)

в) Стержень конечной длины

Для стержня конечной длины дифференциальное уравнение (2.22) и его решение (2.23) сохраняют силу, но граничные условия будут другими:

При х=0 = ₁;

при x=l (2.27)

или

где — температура на конце стержня; 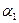— коэффициент теплоотдачи с торца стержня.

При х =l имеет место равенство количества тепла, подведенного к торцу стержня за счет теплопроводности и количества тепла, сдавае­мого поверхностью торца в окружающую среду за счет теплоотдачи.

Если теплоотдачей с конца стержня можно пренебречь, то гранич­ные условия (2.27) можно записать в следующем виде:

при х = 0 = ₁;

при x=l (2.28)

= _l

Для определения постоянных С₁ и С₂ граничные условия (2.28) под­ставляем в уравнение (2.23):

при х = 0 ₁=C₁+C₂;
при х=l

Из полученных уравнений определяем постоянные С₁ и С₂:

Подставляя полученные значения Cx и С2 в уравнение (2.23) получаем

: (2.29)

 

Умножим и разделим правую часть уравнения (2.29) на e^-ml, тогда

Напомним, что

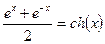и сh(x)

Тогда уравнение (2.29) может быть записано в следующем виде:

, град. (2.30)

По формуле (2.30) можно вычислить температуру в любом сече­нии стержня. В предельном случае, когда х=l, формула (2.30) при­нимает вид:

, град.

Для случая, когда теплоотдачей с торца нельзя пренебрегать, гра­ничные условия выражаются равенством (2.27). Определив постоянные С₁ и С₂ из указанных граничных условий, получим:

град. (2.31)

Из уравнения (2.31) следует, что (2.30) есть частный случай общего за­кона распределения температуры в стержне, выраженного уравнением (2.31). Действительно, если пренебречь теплоотдачей с торца стержня

и принять = 0, то уравнение (2.31) переходит в уравнение (2.30).

Количество тепла, отдаваемое поверхностью ребра в окружающую среду, будет равно количеству тепла, подводимому к основанию ребра

 

 

Из уравнения (2.30) находим:

Тогда

, вт (2.32)

 

Подставив в (2.32), получим

(2.32a)

Если длина стержня очень велика, то ch(ml)→∞, a th(ml) 1. Тогда

и формула (2.32а) превращается в (2.26).