Описание численных методов решения нелинейных уравнений

Это описание приведено для решения некоторых задач.

Решение нелинейных уравнений вида

F(x)=0 (1)

Заключается в отыскании одного или всех корней на отрезке [a, b] изменения х. Обычно стараются локализовать каждый корень на своем отрезке[a, b]. Тогда нахождение всех корней сводится к локализации каждого корня с последующим сужением отрезка одним из описанных ниже методов.

 

Метод простых итераций

Метод основан на представлении уравнения (1) в виде

x=f(x) (2)

и многократном применении итерационной формулы x_n+1= f(x_n) до тех пор, пока соблюдается условие

(3)

где e - заданная погрешность вычисления корня х.

 

Метод Ньютона (касательных)

Метод основан на замене F(x) в точке начального приближения x=x₀ касательной, пересечение которой с осью х дает первое приближение х₁ и т.д. Таким образом, итерационный процесс схождения к корню реализуется формулой

x_n+1=x_n-F(x_n)/F'(x_n),

до тех пор, пока соблюдается условие (3)

 

Метод деления отрезка

Метод деления отрезка пополам реализуется следующим алгоритмом (а и b – это концы отрезка, на котором ищется корень):

 

Для F(a)>0

1. Вычисляется x=(a+b)/2

2. Вычисляется F(x)

3. Если F(x)>0 ,задаем a=х, иначе b=x

4. Проверяется условие b-a>e; если оно выполняется, следует перейти к п.1, если не выполняется, вычисления заканчиваются.

 

Если F(a)<0, то алгоритм следующий:

1. Вычисляется x=(a+b)/2

2. Вычисляется F(x)

3. Если F(x)>0 ,задаем b=х, иначе a=x

4. Проверяется условие b-a>e; если оно выполняется, следует перейти к п.1, если не выполняется, вычисления заканчиваются.

 

Возврат на содержание

Пример решения задачи

Условие задачи: сумму восьмеричных чисел 17+1700+170000+17000000 представить в шестнадцатеричной системе счисления. Найти в записи полученного числа пятую цифру слева.

 

Таблица используемых переменных:

 

Идентификатор переменной или функции	Назначение в программе	Тип
а	Число, равное сумме восьмеричных чисел	Длинный целый
i, j	Параметры циклов	Целые
х	Ссылка на переменную i для изменения ее значения функцией
rez [10]	Число в 16 с/с в виде массива из цифр и букв	Символьный
к	Номер цифры в записи числа в 16 с/с	Целый
step	Функция возведения натурального числа в натуральную степень	Длинный целый
x	Формальная переменная функции step, основание степени	Целый
y	Формальная переменная функции step, показатель степени	Целый
i	Локальная переменная функции step, счетчик цикла	Целый
pr	Локальная переменная функции step, произведение натуральных чисел	Длинный целый
per8_10	Функция перевода числа из 8 с/с в 10 с/с	Длинный целый
b	Формальная переменная функции per8_10, число в 8 с/с	Длинный целый
k	Локальная переменная функции per8_10, остаток деления числа на 10	Длинный целый
nov	Локальная переменная функции per8_10, новое число в 10 с/с	Длинный целый
i	Локальная переменная функции per8_10, параметр цикла	Целый
per10_16	Функция перевода числа из 10 с/с в 16 с/с	Пустой
а	Формальная переменная функции per10_16, число в 10 с/с
v [10 ]	Формальный параметр функции per10_16, массив из цифр и букв в 16 с/с	Символьный
&i	Ссылка на переменную i, значение которой изменяется в функции per10_16 и передается в главную функцию
ost	Локальная переменная функции per10_16, остаток деления числа на 16	Целый

 

Текст программы:

 

# include <iostream.h>

/* функция возведения натурального числа в натуральную степень */

long step(long x, int y)

{

int i; long pr;

pr = 1;

if (y= =0) return pr;

else

for (i=1; i<=y; i++) pr*=x;

return pr;

/* функция перевода числа из 8 с/с в 10 с/с */

long per8_10(long b)

{

long k, nov; int i;

nov = 0; i = 0;

while (b>0) do

{

k = b % 10;

b /= 10;

nov += k*step(8, i);

i++;

}

return nov;

}

/* функция перевода числа из 10 с/с в 16 с/с */

void per10_16(long a, char v[10], int &i)

{

int ost;

i = 1;

do

{

ost = a % 16;

a /= 16;

switch (ost) {

case 0: v[ i ] = ‘0’; case 8 : v[ i ] = ‘8’;

case 1 : v[ i ] = ‘1’; case 9 : v[ i ] = ‘9’;

case 2 : v[ i ] = ‘2’; case 10 : v[ i ] = ‘A’;

case 3 : v[ i ] = ‘3’; case 11 : v[ i ] = ‘B’;

case 4 : v[ i ] = ‘4’; case 12 : v[ i ] = ‘C’;

case 5 : v[ i ] = ‘5’; case 13 : v[ i ] = ‘D’;

case 6 : v[ i ] = ‘6’; case 14 : v[ i ] = ‘E’;

case 7 : v[ i ] = ‘7’; case 15 : v[ i ] = ‘F’;

}

i++;

}

while (a<1);

}

 

void main (void)

{

int i = 1, j, k, &x = i; long a;

char rez, v[10];

a = per8_10(17)+per8_10(1700)+per8_10(170000)+per8_10(17000000);

per10_16(a, v, x);

/* a – число в 10 с/с, равное сумме исходных восьмеричных чисел,

v – символьный массив из цифр числа в 16 с/с,

x – ссылка на переменную i – количество цифр числа в 16 с/с*/

k = 1;

cout << “ в результате получено следующее число в 16 с/с:” ;

for ( j = i – 1; j > 0; j – –)

{

rez[ k ] = v[ j ]; cout << rez[ k ]; k++;

}

cout << “\nпятая цифра слева в записи этого числа:”<< rez[5];

}

 

 

Блок – схема данного алгоритма:

 

 

 

 

 

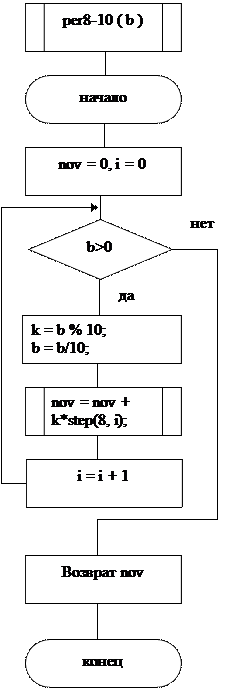
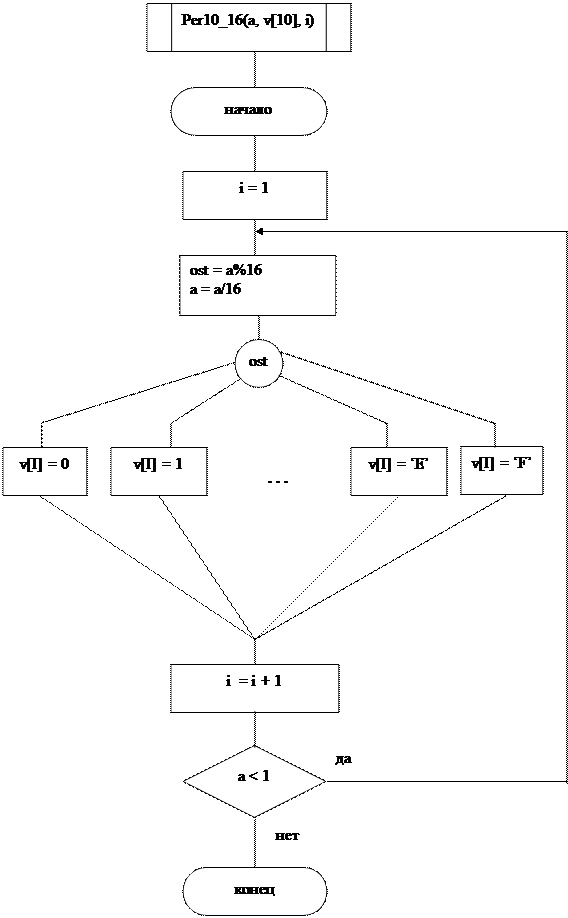
Возврат на содержание

Варианты заданий

 

Варианты заданий см. в папке “ЗАДАНИЯ НА ЛАБОРАТОРНЫЕ И КУРСОВУЮ РАБОТЫ” (в папке с именем группы)

 

Список литературы:

 

1. Березин Б. И., Березин С. Б. Начальный курс С и С++. – М.: Диалог – Мифи, 1996. – 288 с.

2. Крис Джамса Учимся программировать на языке С++. – Пер. с англ. – М.: Мир, 1997. – 320 с.

3. Страуструп Б. Язык программирования Си++. – Пер. с англ. – М.:Радио и связь, 1991. – 352 с.

4. Бруно Бабэ Просто и ясно о Borland C++. – Пер. с англ. – М.: Бином, 1996, - 416 с.

5. Ален И. Голуб С и С++. Правила программирования. – Пер. с англ. – М.: Бином, 1996. – 272 с.

6. Симонович С.В. и др. Информатика. Базовый курс. – СПб: Питер, 2000. – 640 с.

7. Абрамов С. А., Гнездилова Г. Г., Капустина Е. Н., Селюн М. И. Задачи по программированию. – М.: Наука, 1988. – 224 с.