 |
Главная |
Параболическая регрессия
|
из
5.00
|
Рассмотрим построение уравнения регрессии вида 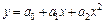 .
.
Составление системы нормальных уравнений для нахождения коэффициентов параболической регрессии осуществляется аналогично составлению нормальных уравнений линейной регрессии.

После преобразований получаем:
 .
.
Решая систему нормальных уравнений, получают коэффициенты уравнения регрессии.
Далее рассчитывают остаточную дисперсию  .
.
 ,
,
где  , а
, а  .
.
Уравнение второй степени значимо лучше описывает экспериментальные данные, чем уравнение первой степени, если уменьшение дисперсии  по сравнению с дисперсией линейной регрессии
по сравнению с дисперсией линейной регрессии  является значимым (неслучайным). Значимость различия между
является значимым (неслучайным). Значимость различия между  и
и  оценивается критерием Фишера:
оценивается критерием Фишера:
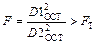 ,
,
где число  берется по справочным статистическим таблицам (приложение 1) соответственно степеням свободы
берется по справочным статистическим таблицам (приложение 1) соответственно степеням свободы  и выбранного уровня значимости
и выбранного уровня значимости  .
.
Порядок выполнения расчетной работы:
1. Ознакомиться с теоретическим материалом, изложенным в методических указаниях либо в дополнительной литературе.
2. Рассчитать коэффициенты линейного уравнения регрессии 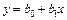 . Для этого необходимо вычислить суммы
. Для этого необходимо вычислить суммы  . Удобно сразу вычислить суммы
. Удобно сразу вычислить суммы 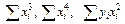 , которые пригодятся для расчета коэффициентов параболического уравнения.
, которые пригодятся для расчета коэффициентов параболического уравнения.
3. Вычислить расчетные значения выходного параметра по уравнению  .
.
4. Вычислить общую и остаточную дисперсии 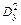 ,
,  , а также критерий Фишера
, а также критерий Фишера  .
.
5. Рассчитать коэффициенты параболического уравнения регрессии 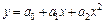 . Учитывая сложность решения системы нормальных уравнений, рекомендуется записать систему нормальных уравнений в матричной форме:
. Учитывая сложность решения системы нормальных уравнений, рекомендуется записать систему нормальных уравнений в матричной форме:
 ,
,
где  – матрица, элементами которой являются коэффициенты системы нормальных уравнений;
– матрица, элементами которой являются коэффициенты системы нормальных уравнений;
 – вектор, элементами которого являются неизвестные коэффициенты;
– вектор, элементами которого являются неизвестные коэффициенты;
 – матрица правых частей системы уравнений.
– матрица правых частей системы уравнений.
6. Далее решить эту систему линейных уравнений в среде MathCad. Для этого воспользоваться стандартной функцией для решения системы линейных уравнений  .
.
7. Вычислить расчетные значения выходного параметра по уравнению  .
.
8. Вычислить остаточную дисперсию  , а также критерий Фишера
, а также критерий Фишера  .
.
9. Сделать выводы.
10. Построить графики уравнений регрессии и исходных данных.
11. Оформить расчетную работу.
Пример расчета.
По экспериментальным данным зависимости плотности водяного пара от температуры  получить уравнения регрессии вида
получить уравнения регрессии вида  и
и  . Провести статистический анализ и сделать вывод о лучшей эмпирической зависимости.
. Провести статистический анализ и сделать вывод о лучшей эмпирической зависимости.

| ||||||||

| 0,0512 | 0,0687 | 0,081 | 0,1546 | 0,2516 | 0,3943 | 0,5977 | 0,8795 |
Обработка экспериментальных данных проведена в соответствии с рекомендациями к работе. Расчеты для определения параметров линейного уравнения приведены в таблице 1.
Таблица 1 – Нахождение параметров линейной зависимости вида

| ||||||||
Плотность водяного пара на линии насыщения 
| ||||||||
| № | ti,°C |  , ом , ом
| ti2 | 
|  расч. расч.
| 
| 
| 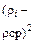
|
| 0,0512 | 2,05 | -0,0403 | -0,0915 | 0,0084 | 0,0669 | |||
| 0,0687 | 3,16 | 0,0248 | -0,0439 | 0,0019 | 0,0582 | |||
| 0,0811 | 4,22 | 0,0899 | 0,0089 | 0,0001 | 0,0523 | |||
| 0,1546 | 9,9 | 0,2202 | 0,06565 | 0,0043 | 0,0241 | |||
| 0,2516 | 19,12 | 0,3505 | 0,09894 | 0,0098 | 0,0034 | |||
| 0,3943 | 34,70 | 0,4808 | 0,08654 | 0,0075 | 0,0071 | |||
| 0,5977 | 59,77 | 0,6111 | 0,01344 | 0,0002 | 0,0829 | |||
| 0,8795 | 98,50 | 0,7414 | -0,13807 | 0,0191 | 0,3245 | |||
| сумма | 2,4786 | 231,41 | 0,0512 | 0,6194 | ||||
| среднее | 72,25 | 0,3098 | 5822,5 | 28,93 | ||||
| b0= | -0,4747 | D1ост2= | 0,0085 | |||||
| b1= | 0,0109 | Dy2= | 0,0885 | |||||
| F= | 10,368 | |||||||
 FT=3,87 F>FT модель адекватна FT=3,87 F>FT модель адекватна
|

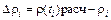


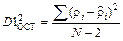
 .
.
Для определения параметров параболической регрессии  вначале были определены элементы матрицы коэффициентов и матрицы правых частей системы нормальных уравнений. Затем расчет коэффициентов выполнен в среде MathCad:
вначале были определены элементы матрицы коэффициентов и матрицы правых частей системы нормальных уравнений. Затем расчет коэффициентов выполнен в среде MathCad:

Данные расчетов приведены в таблице 2.
Обозначения в таблице 2:

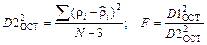 .
.
Выводы
Параболическое уравнение значимо лучше описывает экспериментальные данные зависимости плотности пара от температуры, так как расчетное значение критерия Фишера  значительно превышает табличное равное 4,39. Следовательно, включение квадратичного члена в полиномиальное уравнение имеет смысл.
значительно превышает табличное равное 4,39. Следовательно, включение квадратичного члена в полиномиальное уравнение имеет смысл.
Полученные результаты представлены в графическом виде (рис.3).

Рисунок 3 – Графическая интерпретация результатов расчета.
Пунктирная линия – уравнение линейной регрессии; сплошная линия – параболической регрессии, точки на графике – экспериментальные значения.
| Таблица 2. – Нахождение параметров зависимости вида y(t)=a0+a1∙x+a2∙x2 | Плотность водяного пара на линии насыщения ρ= a0+a1∙t+a2∙t2 | (ρi–ρср)2 | 0,0669 | 0,0582 | 0,0523 | 0,0241 | 0,0034 | 0,0071 | 0,0829 | 0,03245 | 0,6194 | |||||
| (Δρ)2 | 0,0001 | 0,0000 | 0,0000 | 0,0002 | 0,0000 | 0,0002 | 0,0002 | 0,0002 | 0,0010 | 0,0085 | 0,0002 | 0,0885 | 42,5 | |||
| ∆ρi=ρ(ti)расч–ρi | 0,01194 | –0,00446 | –0,00377 | –0,01524 | –0,00235 | 0,01270 | 0,011489 | –0,01348 | D12ост= | D22ост= | D12y= | F= | ||||
| ρ(ti)расч. | 0,0631 | 0,0642 | 0,0773 | 0,1394- | 0,2493 | 0,4070 | 0,6126 | 0,8660 | 2,4788 | |||||||
| ti2ρi | 81,84 | 145,33 | 219,21 | 633,24 | 1453,2 | 3053,4 | 5977,00 | 11032,45 | 22595,77 | |||||||
| ti4 | ||||||||||||||||
| ti 3 | ||||||||||||||||
| tiρi | 2,05 | 3,16 | 4,22 | 9,89 | 19,12 | 34,70 | 59,77 | 98,50 | 231,41 | |||||||
| ti2 | ||||||||||||||||
| ρ, ом | 0,0512 | 0,0687 | 0,0811 | 0,1546 | 0,2516 | 0,3943 | 0,5977 | 0,8795 | 2,4786 | 0,3098 | ||||||
| ti,°C | 0,36129 | –0,0141 | 1,6613E-04 | |||||||||||||
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | сумма | среднее | a0= | a1= | a2= |
Приложение 1
Таблица распределения Фишера при q = 0,05
| f2 | — | |||||||||
| f1 | ||||||||||
| 161,40 | 199,50 | 215,70 | 224,60 | 230,20 | 234,00 | 238,90 | 243,90 | 249,00 | 254,30 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,76 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,24 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,82 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,52 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,17 | 2,02 | 1,88 | 1,61 | 1,25 |
|
из
5.00
|
Обсуждение в статье: Параболическая регрессия |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

