 |
Главная |
Экспериментальная часть
|
из
5.00
|
 Рис. 1
Рис. 1
|
В нашей работе момент инерции тела определяется при помощи трифилярного повеса (рис. 1), который представляет собой круглую платформу, подвешенную на трех симметрично расположенных проволоках, укрепленных у краев платформы. Наверху эти проволоки также симметрично прикреплены к трем точкам треноги, расположенным по окружности меньшего радиуса. Платформа может совершать крутильные колебания вокруг вертикальной оси, перпендикулярной к ее плоскости и проходящей крез ее середину: центр тяжести платформы при этом перемещается по оси вращения. Период колебаний определяется моментом инерции платформы. Он будет другим, если платформу нагрузить каким-либо телом. Этим и пользуются в данной работе.
Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h, то ее потенциальная энергия в крайнем положении
П = mgh ,
где g - ускорение свободного падения тела.
Вращаясь в другом направлении, платформа придет в положение равновесия с кинетической энергией
 ,
,
Где I- момент инерции платформы;
 - угловая скорость платформы в момент достижения ею положения равновесия.
- угловая скорость платформы в момент достижения ею положения равновесия.
Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем:

Считая, что платформа совершает гармонические колебания, можно написать зависимость угла поворота платформы от времени:
 , где:
, где:
 - мгновенное значение угла поворота платформы
- мгновенное значение угла поворота платформы
 - амплитудное значение угла поворота
- амплитудное значение угла поворота
Т - период полного колебания
t- время
Угловая скорость  является первой производной от угла поворота
является первой производной от угла поворота  по времени:
по времени:
 .
.
В момент прохождения через положение равновесия абсолютное значение угловой скорости будет максимальным:

Подставляя это значение в уравнение (2) получим:
 .
.
Чтобы найти момент инерции Iплатформы из этого соотношения, выразим высоту подъема платформы hчерез известные величины.
При повороте платформы на угол  центр тяжести ее переместится из точки О в точку О1 (рис. 2), причем
центр тяжести ее переместится из точки О в точку О1 (рис. 2), причем

Так как 
и  ,
,
получим: 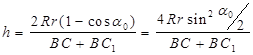
Рис. 2 |
| В |
| r |
При малых углах поворота  (а только в этих случаях колебания можно считать гармоническими) можно положить, что
(а только в этих случаях колебания можно считать гармоническими) можно положить, что 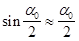 , а сумма
, а сумма  .
.
Учитывая это, получаем  , где R - расстояние от оси платформы до точек закрепления проволок на платформе; r - расстояние от оси платформы до точек закрепления проволок на треноге; l - длина проволок подвеса.
, где R - расстояние от оси платформы до точек закрепления проволок на платформе; r - расстояние от оси платформы до точек закрепления проволок на треноге; l - длина проволок подвеса.
Подставляя значение h, получим:
| О1 |
| C |
| C1 |

|
 , откуда
, откуда  .
.
| А |
| R |
| A1 |
| О |
По этой формуле может быть определен момент инерции платформы и тела, положенного на нее, так как все величины в правой части могут быть непосредственно измерены. В случае нагруженной платформы массу m берут равной сумме масс платформы и тела. Вычисленный момент инерции системы Iсист складывается из момента инерции пустой платформы и тела:
Iсист = I0+IT , где I0 - момент инерции платформы, IT - момент инерции тела.
Отсюда получаем: IT = Iсист - I0
|
из
5.00
|
Обсуждение в статье: Экспериментальная часть |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


