Теоретическое обоснование. Основы программирования и графические возможности системы MATLAB

Основы программирования и графические возможности системы MATLAB

Цель и содержание работы:познакомиться с элементами программирования и возможностями графической визуализации вычислений в пакете MATLAB.

 

Теоретическое обоснование

Программирование в системе MATLAB является эффективным средством ее расширения и адаптации к решению специфических проблем. Оно реализуется с помощью языка программированиясистемы. Большинство объектов этого языка, в частности все команды, операторы и функции, одновременно являются объектами входного языкаобщения с системой в командном режиме работы.

С позиций программиста язык программирования системы является типичным проблемно-ориентированнымязыком программирования высокого уровня. Точнее говоря, это даже язык сверхвысокогоуровня, содержащий сложные операторы и функции, реализация которых на обычных языках (например, Бейсике, Паскале или Си) потребовала бы много усилий и времени. К таким функциям относятся матричные функции, функции быстрого преобразования Фурье и др., а к операторам — операторы построения разнообразных графиков, генерации матриц определенного вида и т. д.

Программами в системе MATLAB являются М-файлы текстового формата, содержащие запись программ в виде программных кодов. Язык программирования системы MATLAB имеет следующие средства:

- данные различного типа;

- константы и переменные;

- операторы, включая операторы математических выражений;

- встроенные команды и функции;

- функции пользователя;

- управляющие структуры;

- системные операторы и функции;

- средства расширения языка.

Коды программ в системе MATLAB пишутся на языке высокого уровня, достаточно понятном для пользователей умеренной квалификации в области программирования. Язык программирования MATLAB является типичным интерпретатором.Это означает, что каждая инструкция программы распознается и тут же исполняется, что облегчает обеспечение диалогового режима общения с системой.

Язык программирования системы MATLAB вобрал в себя все средства, необходимые для реализации различных видов программирования: процедурного, операторного, функционального, логического, структурного (модульного), объектно-ориентированного, визуально-ориентированного.

В основе процедурного,операторногои функциональноготипов программирования лежат процедуры, операторы и функции, используемые как основные объекты языка. Эти типы объектов присутствуют в MATLAB. Логическоепрограммирование реализуется в MATLAB с помощью логических операторов и функций. Это позволяет реализовать основные идеи логического программирования, хотя на выдающуюся роль в этом классе языков программирования MATLAB не претендует.

Зато MATLAB представляет собой яркий пример плодотворности структурногопрограммирования. Подавляющее большинство функций и команд языка представляют собой вполне законченные модули, обмен данными между которыми происходит через их входные параметры, хотя возможен обмен информацией и через глобальные переменные. Программные модули оформлены в виде текстовых М-файлов, которые хранятся на диске и подключаются к программам по мере необходимости. Важно отметить, что в отличие от многих языков программирования, применение тех или иных модулей не требует предварительного объявления, а для создания и отладки самостоятельных модулей MATLAB имеет все необходимые средства. Подавляющее большинство команд и функций системы MATLAB поставляется в виде таких модулей.

Объектно-ориентированноепрограммирование также широко представлено в системе MATLAB. Оно особенно актуально при программировании задач графики. Что качается визуально-ориентированногопрограммирования, то в MATLAB оно представлено в основном в пакете моделирования заданных блоками устройств и систем Simulink.

В MATLAB реализованы возможности по организации циклов и использованию условных операторов.

Условный оператор if в общем виде записывается следующим образом:

if Условие

Инструкции_1

else

Инструкции_2

end

 

Работа условного оператора аналогично работе условного оператора в языке Visual Basic,

Циклы типа for...end обычно используются для организации вычислений с заданным числом повторений. Конструкция такого цикла имеет следующий вид:

for счетчик=Выражение.

Инструкция_1

.

.

Инструкция_N

end

Выражение чаще всего записывается в виде s:d:e, где s — начальное значение счетчика цикла, d — приращение этой переменной и е — конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s :е (в этом случае d=l). Список выполняемых в цикле инструкций завершается оператором end.

Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса. Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.

MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками.

Графики MATLAB строит в отдельных окнах Figure, называемых графическими окнами. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рисунке 9.1. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.

Рисунок 9.1 – Пример построения графика синусоиды

 

Графики в MATLAB можно строить как в командном режиме из Окна команд, так и вызывая их из М-файлов. Для построения двумерных графиков используется команда plot. В общем случае синтаксис команды plot выглядит следующим образом: plot(x, y, ’цвет_стиль_маркер‘),

где x – аргумент функции;

y – значение функции;

цвет и стиль линий графика, также маркер определены в таблице 9.1.

Таблица 9.1 – Цвет, тип линии и тип точки на графике

Цвет	Тип маркера	Стиль линии
r	Красный	.	Точка	-	Сплошная
y	Желтый	о	Окружность	;	Двойной пунктир
g	Зеленый	X	Крест	-.	Штрих-пунктир
c	Голубой	+	Плюс	--	Штриховая
b	Синий	*	Звездочка
m	Фиолетовый	S	Квадрат
k	Черный	D	Ромб
w	Белый	V	Треугольник (вниз)
	^	Треугольник (вверх)
<	Треугольник (влево)
>	Треугольник (вправо)
p	Пятиугольник
H	Шестиугольник

Вызов функции plot с многочисленными парами x и y создает многочисленные графики. При этом MATLAB автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает сам пользователь), что позволяет различать заданные наборы данных. Например

plot(t, f, ‘r-*’, t, y ‘b--+’, t, s, ‘g-.o’) – в этом случае на одной координатной плоскости будут выведены графики трех функций: f(t) – красный с маркером *; y(t) – синий с маркером +; s(t) – зеленый с маркером о. При этом стиль линий также будет различным. Если не указывать параметры ‘цвет_стиль_маркер’, то цвет будет присвоен автоматически, линия будет сплошной, а маркер отсутствовать.

Функции xlabel, ylable, zlable добавляют подписи к соответствующим осям, функция title добавляет заголовок в верхнюю часть окна, а функция text вставляет текст в любое место графика.

Трехмерные поверхности обычно описываются функцией двух переменных z(x, у). Специфика построения трехмерных графиков требует не просто задания ряда значений х и у, то есть векторов х и у. Она требует определения для X и Y двумерных массивов — матриц. Для создания таких массивов служит функция meshgrid. В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid создает матрицы Х и Y, состоящие из повторяющихся строк и столбцов соответственно. Строки матрицы Х дублируют вектор х, а столбцы Y – вектор y. Синтаксис функции meshgrid: [X,Y] = meshgrid(x,y)

Для построения графиков поверхностей используются функции mesh и surface. MATLAB определяет поверхность как z координаты точек над координатной сеткой плоскости x – y, используя прямые линии для соединения соседних точек. Функции mesh и surface отображают поверхность в трех измерениях. При этом mesh создает каркасную поверхность, где цветные линии соединяют только заданные точки, а функция surface вместе с линиями отображает в цвете и саму поверхность.

Для установки палитры цветов трехмерных графиков служит команда colormap, записываемая в следующей форме

сolormap цвет,

где параметр «цвет» может принимать следующие значения

hsv — цвета радуги;

hot — чередование черного, красного, желтого и белого цветов;

gray — линейная палитра в оттенках серого цвета;

bone — серые цвета с оттенком синего;

copper — линейная палитра с оттенками меди;

pink — розовые цвета с оттенками пастели;

white— палитра белого цвета;

flag — чередование красного, белого, синего и черного цветов;

lines — палитра с чередованием цветов линий;

colorcube — расширенная палитра RGB;

jet — разновидность палитры HSV;

prism — призматическая палитра цветов;

cool — оттенки голубого и фиолетового цветов;

autumn — оттенки красного и желтого цветов;

spring — оттенки желтого и фиолетового цветов;

winter — оттенки синего и зеленого цветов;

summer — оттенки зеленого и желтого цветов.

 

Уже построенные графики удобно редактировать в графическом окне Figure. Для этого используется панель инструментов, с помощью которой можно менять толщину, цвет, маркер линий. Также на панели инструментов есть «графическая лупа» («+» « – » ), позволяющая увеличивать и уменьшать отдельные части графика.

В одном графическом окне можно одновременно вывести несколько графиков. Для этого графическое окно разбивается на необходимое количество окон командой

subplot(m,n,p) или subplot(m n p)

Эта команда разбивает графическое окно на т х п подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, а р— номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам). Например

» х=-5:0.1:5;

subplot(1.2.1), plot(x.sin(x))

subplot(1.2.2), plot(sin(5*x).cos(2*x+0.2))

При этом графическое окно разобьется на два подокна в первом будет выведен график функции sin(x), во втором – зависимость cos(2x+0,2) от sin(5x).

Задание

1. Создать файл-сценарий с программой для решения следующей задачи. Для восьми различных наборов значений коэффициентов:

а= [-1 2 5 8 10 -4 -11 12], b= [2 -4 12 9 -11 -3 6 10] и с= [4 2 3 -2 -4 7 11 2] найти корни квадратного уравнения . Из найденных корней сформировать два массива X1 и X2.

2. Построить график функции одной переменной y=sin(x). Построить несколько графиков, sin(x) и cos(x). в одной координатной плоскости.

3. Построить графики зависимости массивов Х1 и Х2 от номера набора коэффициентов квадратного уравнения. Отредактировать графики.

4. Построить графики функций двух переменных: 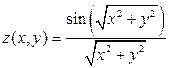, где x и y изменяются от -8 до 8 с шагом 0,5;

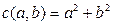, где a и b изменяются от -5 до 5 с шагом 0,15