Треугольник Серпинского

ФАКУЛЬТЕТ КИБЕРНЕТИКИ

 

Курсовая работа по материаловедению

«Фракталы»

 

Выполнили:

студенты гр. КС-71-10

Салтыков Егор

Лытенкова Дарья

 

Проверил:

Смирнов Александр Николаевич

 

Москва

2011-2012

Содержание:

1. Введение.

2. Определение фракталов.

3. Из истории изучения фракталов.

4. Классификация фракталов.

5. Геометрические фракталы.

6. Алгебраические фракталы.

7. Стохастические фракталы.

8. Фракталовые деревья.

9. Измерение тел.

10. Дробная размерность.

11. Практический расчет размерности.

12. Чем актуальны фракталы.

13. Вывод.

Введение

В данной курсовой работе рассматриваются основные вопросы, связанные с фракталами, такие как определение фракталов, их размерность, применение, а также история открытия.

В качестве примера приведен расчет размерности фрактала дистиллированной воды. При расчете был использован калькулятор размерности, так же приведены некоторые общие сведения о фракталах.

Фракталами называют бесконечно самоподобные фигуры, каждый фрагмент которых повторяется при уменьшении масштаба. Разветвления трубочек трахей, нейроны, сосудистая система человека, извилины берегов морей и озер, контуры деревьев — это все фракталы. Фракталы находят в местах таких малых, как клеточная мембрана, и таких огромных, как звездные галактики. Можно сказать, что фракталы – это уникальные объекты, порожденные непредсказуемыми движениями хаотического мира!

Из истории изучения фракталов

Термин «фрактал» был введен Б.Мандельбротом в 1975 г.. Согласно Мандельброту, фракталом (от лат. «fractus» - дробный, ломанный, разбитый) называется структура, состоящая из частей, подобных целому. Свойство самоподобия резко отличает фракталы от объектов классической геометрии. Термин самоподобие означает наличие тонкой, повторяющийся структуры, как на самых малых масштабах объекта, так и в макромасштабе.

История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса – самые наглядные, потому что в них сразу видно самоподобие. Примерами таких фракталов служат: кривые Коха, Леви, Минковского, треугольник Серпинского, губка Менгера, дерево Пифагора (Рис.1) и др. С математической точки зрения, фрактал - это, прежде всего, множество с дробной (промежуточной, «не целой») размерностью. В то время как гладкая евклидова линия заполняет в точности одномерное пространство, фрактальная кривая выходит за пределы одномерного пространства, вторгается за границы в двумерное пространство. Таким образом, фрактальная размерность кривой Коха будет находиться между 1 и 2. Это, прежде всего, означает, что у фрактального объекта невозможно точно измерить его длину!

Существует множество классификаций фракталов. Принято различать регулярные и нерегулярные фракталы, из которых первые являются плодом воображения (математическая абстракция), подобным снежинке Коха или треугольнику Серпинского, а вторые - продуктом природы или деятельности человека. Нерегулярные фракталы (рис.2) в отличие от регулярных сохраняют способность к самоподобию в ограниченных пределах, определяемых реальными размерами системы.

Фракталы находят все большее и большее применение в науке и технике. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Можно до бесконечности приводить примеры фрактальных объектов в природе, - это и облака, и хлопья снега, и горы, и вспышка молнии, и наконец, цветная капуста. Фрактал как природный объект - это вечное непрерывное движение, новое становление и развитие.

Кроме того, фракталы находят применение в децентрализованных компьютерных сетях и «фрактальных антеннах». Весьма интересны и перспективны для моделирования различных стохастических (не детерминированных) «случайных» процессов, так называемые «броуновские фракталы». В случае нанотехнологии фракталы тоже играют важную роль, поскольку из-за своей иерархической самоорганизации многие наносистемы обладают нецелочисленной размерностью, то есть являются по своей геометрической, физико-химической или функциональной природе фракталами. Например, ярким примером химических фрактальных систем являются молекулы «дендримеров». Кроме того, принцип фрактальности (самоподобной, скейлинговой структуры) является отражением иерархичности строения системы и поэтому является более общим и универсальным, чем стандартные подходы к описанию строения и свойств наносистем.

Классификация фракталов

•Алгебраические фракталы

•Множество Мандельброта

•Множество Жюлиа

•Бассейны (фракталы) Ньютона

•Биоморфы

•Треугольники Серпинского

•Геометрические фракталы

•Кривая Коха (снежинка Коха)

•Кривая Леви

•Кривая Гильберта

•Ломаная (кривая) дракона (Фрактал Хартера-Хейтуэя)

•Множество Кантора

•Треугольник Серпинского

•Ковёр Серпинского

•Дерево Пифагора

•Круговой фрактал

•Стохастические фракталы

•Рукотворные фракталы

•Природные фракталы

•Детерминированные фракталы

•Недетерминированные фракталы

Геометрические фракталы

Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фрактал.

Рассмотренная выше кривая Пеано является геометрическим фракталом.

Классические примеры геометрических фракталов - Снежинка Коха, Лист, Треугольник Серпинского).

Снежинка Коха

Из этих геометрических фракталов очень интересным и довольно знаменитым является первый - снежинка Коха. Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны. Получается, что наша бесконечная кривая покрывает ограниченную площадь. Попробуйте сделать то же самое методами и фигурами из евклидовой геометрии. Для построения геометрических фракталов хорошо приспособлены так называемые L-Systems. Суть этих систем состоит в том, что имеется определенных набор символов системы, каждый из которых обозначает определенное действие и набор правил преобразования символов.

Треугольник Серпинского

Второе свойство фракталов - самоподобие. Возьмем, например, треугольник Серпинского. Для его построения из центра треугольника мысленно вырежем кусок треугольной формы, который своими вершинами будет упираться в середины сторон исходного треугольника. Повторим эту же процедуру для трех образовавшихся треугольников (за исключением центрального) и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием.

Драконова ломаная

Драконова ломаная относится к классу самоподобных рекурсивно порождаемых геометрических структур. Ломаная нулевого порядка представляет собой просто прямой угол. Изображение фигуры каждого следующего порядка строится путем рекурсивных замен каждого из отрезков фигуры младшего порядка на два отрезка, сложенных также в виде прямого угла.

При этом каждый первый угол оказывается "вывернутым" наружу, а каждый второй - вовнутрь. Несмотря на внешнюю простоту, построение драконовой ломаной - увлекательная алгоритмическая задачка, решение которой может потребовать от вас определенных мыслительных усилий. На рисунке проиллюстрирован алгоритм построения драконовой ломаной и изображен вполне взрослый "дракон" десятого порядка.

Алгебраические фракталы

 

Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:

С течением времени стремится к бесконечности.

Стремится к 0

Принимает несколько фиксированных значений и не выходит за их пределы.

Поведение хаотично, без каких либо тенденций.

Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта.

Для его построения нам необходимы комплексные числа. Комплексное число - это число, состоящее из двух частей - действительной и мнимой, и обозначается оно a+bi. Действительная часть a это обычное число в нашем представлении, а вот мнимая часть bi интересней. i - называют мнимой единицей. Почему мнимой? А потому, что если мы возведем i в квадрат, то получим -1.

Комплексные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень, нельзя только их сравнивать. Комплексное число можно изобразить как точку на плоскости, у которой координата Х это действительная часть a, а Y это коэффициент при мнимой части b.

На рисунке, изображающем множество Мандельброта я взял небольшой участок и увеличил его до размеров всего экрана (как в микроскоп). Что же мы видим? Проявление самоподобности. Не точной самоподобности, но близкой и с ней мы будем сталкиваться постоянно, увеличивая части нашего фрактала больше и больше. До каких же пор мы можем увеличивать наше множество? Так вот если мы увеличим его до предела вычислительной мощности компьютеров, то покроем площадь равную площади солнечной системы вплоть до Сатурна.

Стохастические фракталы

Типичный представитель данного класса фракталов "Плазма".Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладываем текстуру и пожалуйста фотореалистичные горы готовы.

 

Фрактальные деревья

 

Множество заблуждений связано с фрактальностью деревьев. Древовидные объекты во многом напоминают фракталы: они строятся итеративно, они выглядят фрактально, и иногда они даже являются фракталами. Однако, в большинстве случаев, это сходство является только внешним.

Классические деревья

 

Давайте рассмотрим характерное дерево.

 

Можно ли найти его размерность подобия, как мы это делали в заметке про дробные размерности? Видно, что всё дерево подобно своим частям.

 

Однако не всё дерево можно составить из подобных частей. Каждая ветка действительно подобна дереву (отмечены красным и зелёным), но имеются ещё два отрезка, которые не укладываются о общую схему (чёрные). Таким образом, приведённое здесь дерево не является самоподобным объектом и искать его размерность по полученной ранее формуле нельзя.

 

Тем не менее, легко можно создать деревья, которые будут полностью самоподобны.

Самоподобные деревья

 

Чтобы сделать наше дерево самоподобным, нам просто надо заменить отрезки, которые нарушали самоподобие, на деревья. Например так:

 

Здесь видно, что большое дерево полностью составлено из своих маленьких подобий. Два поддерева имею коэффициент подобия 0.55 (красное и зелёное), а восемь деревьев, составляющих «ветки» — 0.08 (все восемь — чёрные).

 

Размерность этого дерева легко вычисляется и равна примерно 1.3788.

 

Можно сделать ветки более тонкими. Давайте удвоим количество под-деревьев в «ветках» и вдвое уменьшим их размер:

 

Размерность этого фрактала 1.3455.

 

Если мы ещё раз удвоим количество маленьких копий дерева в «ветках» и ещё раз уполовиним размер этих копий, то получим ещё более тонкие ветки:

 

Размерность такого фрактала уже 1.3200.

Самоаффинные деревья

 

Строго говоря, фрактал не обязательно должен быть именно самоподобен. Его фрагменты могут быть получены не только преобразованием подобия, но и любым аффинным преобразование.

 

С помощью аффинных преобразований можно сделать «ветки» тоньше, просто деформировав, составляющие их, части дерева.

 

Про то, как вычисляются размерности самоаффинных объектов я напишу как-нибудь на досуге, а здесь просто скажу, что размерность этого фрактала 1.7251.

Какую же размерность имеют обычные деревья?

 

Подсчёт размерности дерева зависит от того, как вы его строите.

 

Например, вы можете считать, что это самоаффинный фрактал, у которого фракталы-ветки выродились в отрезки. Здесь надо понимать, что ветка, в этом случае, не является просто отрезком. В каждой точке происходит наложение бесконечного числа точек, принадлежащим разным веткам сплюснутого в отрезок фрактала. То есть при таком построении дерево не состоит из отрезков, а строится из гораздо более «тяжёлых» составляющих. Для дерева с рассматриваемыми пропорциями размерность составит 1.1594.

 

Но если вы строите дерево честно — из отрезков, то его размерность будет просто 1. Больше того, если сумма коэффициентов подобия меньше единицы, то можно легко вычислить протяжённость всех веток (по формуле для суммы геометрической прогрессии). То есть дерево становится не просто одномерной линией, но ещё и имеет конечную длину.

Измерение тел

 

Сперва небольшое введение, чтобы привести наши бытовые представления об измерении тел в некоторый порядок. Не стремясь к математической точности формулировок, давайте разберёмся, что же такое размер, мера и размерность. Размер объекта можно померить линейкой. В большинстве случаев размер получается малоинформативен. Какая куча крупы больше?

 

Если сравнивать высоты, то больше красная, если ширины — зелёная.

 

Сравнение размеров может быть информативным если предметы подобны друг другу:

 

Теперь какие бы размеры мы ни сравнили: ширину, высоту, сторону, периметр, радиус вписанной окружности или любые другие, всегда получится, что зелёная куча больше.

 

Далее мы будем говорить о подобных объектах, поэтому «размер» нам пригодится.

 

Мера

 

Мера тоже служит для измерения объектов, но она измеряется не линейкой. О том, как именно она измеряется мы ещё поговорим, а пока отметим её главное свойство — мера аддитивна.

 

Выражаясь на бытовом языке, при слиянии двух объектов, мера суммы объектов равна сумме мер исходных объектов.

 

Для одномерных объектов мера пропорциональна размеру. Если вы возьмёте отрезки длиной 1см и 3см, «сложите» их, то «суммарный» отрезок будет иметь длину 4см (1+3).

 

Для не одномерных тел, мера вычисляется по некоторым правилам, которые подбираются так, чтобы мера сохраняла аддитивность. Например, если вы возьмёте квадраты со сторонами 3см и 4см и «сложите» их, то сложатся площади (9+16=25), то есть сторона (размер) результата будет 5см.

И слагаемые, и сумма являются квадратами, то есть подобны друг другу и мы можем сравнивать размеры. Оказывается, что размер суммы не равен сумме размеров.

 

Как же связаны мера и размер?

 

Размерность

 

Как раз размерность и позволяет связать меру и размер.

 

Давайте обозначим размерность — D, меру — M, размер — L. Тогда формула, связывающая эти три величины будет имеют вид:

 

M = LD

 

 

Для привычных на мер эта формула приобретает всем знакомые обличия. Для двухмерных тел (D=2) мерой (M) является площадь (S), для трёхмерных тел (D=3) — объём (V):

 

S = L2, V = L3

 

Внимательный читатель спросит, по какому праву мы написали знак равенства? Ну хорошо, площадь квадрата равна квадрату его стороны, а площадь круга? Работает ли эта формула для любых объектов?

 

И да и нет. Вы можете заменить равенства на пропорциональности и ввести коэффициенты, а можете считать, что мы вводим размеры тел именно так, чтобы формула работала. Например для круга мы будем называть размером длину дуги равной корень из «пи» радиан. А почему нет?

 

В любом случае, наличие или отсутствие коэффициентов не изменит суть дальнейших рассуждений. Для простоты, я не буду вводить коэффициенты; ^если хотите, вы можете их добавить самостоятельно, повторить все рассуждения и убедиться, что они (рассуждения) не утратили своей справедливости.

Итого

 

Из всего сказанного нам следует сделать один вывод, что если фигуру уменьшить в N раз (отмасштабировать), то она будет укладываться в исходной ND раз. Действительно, если уменьшить отрезок (D=1) в 5 раз, то он поместится в исходном ровно пять раз (51=5); Если треугольник (D=2) уменьшить в 3 раза, то он уложится в исходном 9 раз (3²=9).

Если куб (D=3) уменьшить в 2 раза, то он уложится в исходном 8 раз (2³=8).

Верно и обратное: если при уменьшении размера фигуры в N раз, оказалось, что она укладывается в исходной n раз (то есть мера её уменьшилась в n раз), то размерность можно вычислить по формуле:

 

D = ln(n)/ln(N)

 

 

Не очень строго и опуская многие важные детали, мы всё же получили формулу для размерности.

Дробная размерность

 

Простейший пример

 

Про дробную размерность обычно рассказывают на примерах различных ломаных. Обратимся к звезде Коха.

Процедура её построения показана на рисунке (снизу вверх):

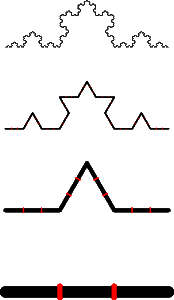
Эти построения повторяются бесконечное число раз и в конце концов у нас получается ломаная, состоящая из бесконечного числа отрезков. Сколько бы мы её не масштабировали, мы всё равно будем получать одно и то же.

Это и есть звезда Коха.

 

Строго говоря, полученное множество точек уже нельзя называть ломаной. По определению, ломаная должна состоять из конечного числа отрезков. Но я буду использовать слово «ломаная» в «нестрогом» понимании.

 

Давайте теперь воспользуемся нашим приёмом, чтобы определить её размерность.

 

Из построения и рисунка видно, что звезду можно разбить на четыре равные части, при этом размер (скажем, длина исходного отрезка) каждой части будет равен трети размера исходной фигуры. То есть будучи уменьшена в три раза, она уложится в себе четыре раза:

 

По аналогии с нашими предыдущими рассуждениями получаем, что размерность равна

 

D = ln(4)/ln(3) ≈ 1.26185950714291487419

 

То есть это уже не просто отрезок или ломаная (длина звезды Коха бесконечна), но и не плоская фигура, полностью покрывающая некоторую площадь.

 

Если мы слегка модифицируем алгоритм построения и будем извлекать не 1/3 отрезка, а 1/9, то ломаная получится более плотной:

Какова же её размерность? Теперь фигура уложится сама в себе четыре раза после уменьшения в 9/4 раза, то есть размерность можно вычислить по той же формуле:

 

D = ln(4)/ln(9/4) ≈ 1.70951129135145477696

 

 

Как видите, «плотность» покрытия сразу отразилась на размерности.

 

Давайте теперь получим более общую формулу для вычисления размерности. Для этого снова рассмотрим пример:

Итерации снова начинаются с одного отрезка. На каждом шаге итерации количество отрезков удваивается. Каждый порождает два новых: один в 0.88 раз меньше (или, вернее больше) родителя, второй — в 0.41 раз. В пределе получается следующее множество:

Давайте вернёмся к первому шагу итераций, на котором мы получили два отрезка, и посмотрим, какая часть фрактала образована из каждого из них.

Если принять, что размер полного фрактала 1, то размер зелёной части (полученной из большего отрезка) будет 0.88, а размер красной (полученной из меньшего) — 0.41.

 

Та формула, которой мы располагаем, уже не годится, так как мы имеем не один, а два коэффициента масштабирования. Но мы можем воспользоваться нашими знаниями о свойства меры, размера и размерности. Мера, как мы помним, аддитивна, то есть мера полного фрактала, равна сумме мер его частей:

 

M0 = M1 + M2

 

И сам фрактал, и его части имеют одинаковую размерность (D) и мы можем выразить меры, через размеры:

 

L0D = L1D + L2D

 

 

А размеры мы знаем. То есть для размерности нашего фрактала мы можем написать уравнение:

 

1D = 0.88D + 0.41D

 

или просто

 

1 = 0.88D + 0.41D

 

 

Решить это уравнение аналитически невозможно, но «приблизительный» ответ можно «подобрать». Для этого вы можете воспользоваться моим on-line-калькулятором размерностей. В нашем случае

 

D ≈ 1.7835828288192

 

Можете проверить.

 

Таким образом, если фрактал образован из N подобных элементов, с коэффициентами подобия k1, k2 ... kN, то его размерность можно найти из уравнения:

 

1 = k1D + k2D + ... + kND

 

 

По этой формуле уже можно рассчитать размерность многих итерационных систем.

 

Обратите внимание, что, если все коэффициенты равны, то наша формула превращается в уже известную простую формулу:

 

1 = kD + kD + ... + kD = N * kD

 

1/N = kD

 

 

D = ln(1/N)/ln(k)

 

или

 

D = ln(N)/ln(1/k)

 

 

Последнее выражение есть наша первая простая формула для вычисления размерности.

 

 

Практический расчет размерности вещества на примере расчета размерности дистиллированной воды.

 

Имеем графическое изображение поверхности воды:

 

 

Разделяем это изображение на подобные себе части. В данном случае проще и актуальнее разделить изображение на квадраты:

 

1.

2.

 

3.

4.

5.

 

6.

 

И, последний квадрат, являющийся исходным, мы уже привели выше.

Подставляем размеры в калькулятор размерностей:

Размерность воды составляет D=1.643594371.

 

Чем актуальны фракталы

 

Большинство систем в природе сочетают два свойства:

во-первых, они очень велики, часто многогранны, многообразны и сложны,

а во-вторых они формируются под действием очень небольшого количества простых закономерностей, и далее развиваются, подчиняясь этим простым закономерностям.

 

Это самые разные системы, начиная от кристаллов и просто кластеров (различного рода скоплений, таких как облака, реки, горы, материки, звёзды), заканчивая экосистемами и биологическими объектами (от листа папоротника до человеческого мозга).

 

Фракталы являются как раз такими объектами: с одной стороны — сложные (содержащие бесконечно много элементов), с другой стороны — построенные по очень простым законам. Благодаря этому свойству, фракталы обнаруживают много общего со многими природными объектами. Но фрактал выгодно отличается от природного объекта тем, что фрактал имеет строгое математическое определение и поддаётся строгому описанию и анализу.

 

Поэтому теория фракталов позволяет предсказать скорость роста корневых систем растений, трудозатраты на осушение болот, зависимость массы соломы от высоты побегов и многое другое.

Пример применения фракталов

 

Летят два облака. Первое отбрасывает тень площадью A, второе — B. Эти облака сливаются в одно. Какова будет площадь C тени этого нового облака?

 

Ответив на этот вопрос, можно уже делать выводы о том, какова же будет суммарная облачность.

Облака двумерные?

 

Если бы облака имели бы размерность 2 (то есть были бы плоскими), то они бы просто объединись и ответ бы был просто суммой

 

C = A + B

 

 

То есть два облака складываются как два куска обоев.

Но это не верно. Суммарное облако станет не только шире и длинней слагаемых, оно станет ещё и выше. При той же массе площадь будет меньше суммарной.

 

Рассматривая облака, уместно считать мерой массу, так как именно этот параметр лучше всего удовлетворяет определению меры.

Облака трёхмерные?

 

Если бы размерность облаков была бы 3 (то есть они бы были монолитные и без пустот), то ответ бы был

 

C^3/2 = A^3/2 + B^3/2

 

 

То есть

 

C = (A^3/2 + B^3/2)2/3

 

 

Если справедливость этого выражения вызывает у вас сомнения, то предлагаю следующую аргументацию (мне бы не хотелось пускаться тут в точное доказательство). Давайте предположим, что облака имеют форму кубов. (Кубы — монолитные и трёхмерные объекты; с таким же успехом можно было бы взять шары, пирамиды или любые другие тела.) Пусть первое облако-куб имеет сторону a метров, а второе — b метров. Когда облака сложатся, то суммарное облако-куб будет иметь сторону c метров и объём равный сумме объёмов исходных облаков:

 

c³ = a³ + b³

 

 

Предположим, что площади теней кубов равны площадям их сторон (это не ограничивает общности рассуждений). Тогда для площадей имеем следующие выражения:

 

A = a²

B = b²

С = с²

 

 

В результате получаем выражение

 

C^3/2 = A^3/2 + B^3/2

 

 

Но и этот ответ не верен, потому, что облака не монолитные.

Размерность облаков

 

Оказывается, что размерность облаков не целая — 2.3. Правильная формула такова:

 

C^2.3/2 = A^2.3/2 + B^2.3/2

 

 

Как видите, у нас есть теория, описывающая объекты нецелой размерности и есть сами объекты и мы успешно применили теорию к этим объектам.

 

Конечно, одной этой формулы не достаточно для предсказания погоды. В реальности облака не только сливаются и разделяются, они появляются и исчезают, растут и уменьшаются, меняют свою структуру... Наша формула описывает лишь одну из составляющих всех возможных превращений. Но эту составляющую она описывает правильно.