Связь напряжённости и потенциала

Электростатическое поле имеет две характеристики: силовую (напряжённость) и энергетическую (потенциал). Напряжённость и потенциал – различные характеристики одной и той же точки поля, следовательно, между ними должна быть связь.

Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и х₁– х₂ = dx , равна qЕ_хdx. Та же работа равна q(φ₁ - φ₂ )= -dφq. Приравнивая оба выражения, можем записать

Е_хdx = -dφ

Повторив аналогичные рассуждения для осей у и z, можем найти вектор :

где - единичные векторы координатных осей х, у, z.

Из определения градиента следует, что

или (12.31)

т.е. напряжённость поля Е равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости Е поля направлен в сторону убывания потенциала.

Установленная связь между напряжённостью и потенциалом позволяет по известной напряжённости поля найти разность потенциалов между двумя произвольными точками этого поля.

Ø Поле равномерно заряженной сферы радиусом R

Напряжённость поля вне сферы определяется по формуле

(r >R)

Разность потенциалов между точками r₁ и r₂ (r₁>R; r₂ >R ) определим, используя соотношение

Потенциал сферы получим, если r₁= R, r₂ → ∞:

 

Ø Поле равномерно заряженного бесконечно длинного цилиндра

Напряжённость поля вне цилиндра (r >R) определяется формулой

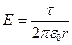
(τ – линейная плотность).

Разность потенциалов между двумя точками, лежащими на расстоянии r₁ и r₂ (r₁>R; r₂ >R ) от оси цилиндра, равна

(12.32)

Ø Поле равномерно заряженной бесконечной плоскости

Напряжённость поля этой плоскости определяется формулой

(σ - поверхностная плотность).

Разность потенциалов между точками, лежащими на расстоянии х₁ и х₂ от плоскости, равна

(12.33)

Ø Поле двух разноименно заряженных бесконечных параллельных плоскостей

Напряженность поля этих плоскостей определяется формулой

Разность потенциалов между плоскостями равна

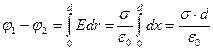(12.34)

(d – расстояние между плоскостями).

 

Примеры решения задач

Пример 12.1. Три точечных заряда Q₁=2нКл, Q₂ =3нКл и Q₃=-4нКл расположены в вершинах равностороннего треугольника со стороной длиной a=10см. Определите потенциальную энергию этой системы.

Дано: Q₁=2нКл=2∙10^-9Кл; Q₂ =3нКл=3∙10^-9Кл; и Q₃=-4нКл=4∙10^-9Кл; a=10см=0,1м.

Найти: U.

Решение:Потенциальная энергия системы зарядов равна алгебраической сумме энергий взаимодействия каждой из взаимодействующих пар зарядов, т.е.

U=U₁₂+U₁₃+U₂₃

где соответственно потенциальные энергии одного из зарядов, находящегося в поле другого заряда на расстоянии а от него, равны

 

; ; (2)

Подставим формулы (2) в выражение (1), найдём искомую потенциальную энергию системы зарядов

Ответ: U=-0,126мкДж.

 

Пример 12.2. Определите потенциал в центре кольца с внутренним радиусом R₁=30см и внешним R₂=60см, если на нём равномерно распределён заряд q=5нКл.

Дано: R₁=30см=0,3м; R₂=60см=0,6м; q=5нКл=5∙10^-9Кл

Найти: φ.

Решение: Кольцо разобьём на концентрические бесконечно тонкие кольца внутренним радиусом r и внешним – (r+dr).

Площадь рассматриваемого тонкого кольца (см.рисунок) dS=2πrdr.

Потенциал в центре кольца, создаваемый бесконечно тонким кольцом,

где – поверхностная плотность заряда.

Для определения потенциала в центре кольца следует арифметически сложить dφ от всех бесконечно тонких колец. Тогда

Учитывая, что заряд кольца Q=σS, где S= π(R₂²-R₁²)- площадь кольца, получим искомый потенциал в центре кольца

Ответ: φ=25В

 

Пример 12.3. Два точечных одноименных заряда (q₁=2нКл и q₂=5нКл) находятся в вакууме на расстоянии r₁= 20см. Определите работу А, которую надо совершить, чтобы сблизить их до расстояния r₂=5см.

Дано: q₁=2нКл=2∙10^-9Кл; q ₂=5нКл=5∙10^-9Кл; r₁= 20см=0,2м; r₂=5см=0,05м.

Найти: А.

Решение: Работа, совершаемая силами электростатического поля при перемещении заряда Q из точки поля, имеющей потенциал φ₁, в точку с потенциалом φ₂.

A₁₂= q(φ₁- φ₂)

При сближении одноимённых зарядов работу совершают внешние силы, поэтому работа этих сил равна по модулю, но противоположна по знаку работе кулоновских сил:

A= -q(φ₁- φ₂)= q(φ₂- φ₁). (1)

Потенциалы точек 1 и 2 электростатического поля

; (2)

Подставив формулы (2) в выражение (1), найдём искомую работу, которую надо совершить, чтобы сблизить заряды,

Ответ: А=1,35 мкДж.

 

Пример 12.4. Электростатическое поле создаётся положительно заряженной бесконечной нитью. Протон, двигаясь под действием электростатического поля вдоль линии напряжённости от нити с расстояния r₁=2см до r₂=10см, изменил свою скорость от υ₁=1Мм/с до υ₂=5Мм/с. Определите линейную плотность τ заряда нити..

Дано: q=1,6∙10^-19 Кл; m=1,67∙10^-27кг; r₁=2см=2∙10^-2м; r₂= 10см=0,1м; r₂=5см=0,05м; υ₁=1Мм/с=1∙10⁶м/с; до υ₂=5Мм/с=5∙10⁶м/с.

Найти:τ.

Решение: Работа, совершаемая силами электростатического поля при перемещении протона из точки поля с потенциалом φ₁ в точку с потенциалом φ₂ идёт на увеличение кинетической энергии протона

q(φ₁- φ₂)=ΔТ (1)

В случае нити электростатическое поле обладает осевой симметрией, поэтому

или dφ=-Edr,

тогда разность потенциалов между двумя точками, находящимися на расстоянии r₁ и r₂ от нити,

(учли, что напряжённость поля, создаваемого равномерно заряженной бесконечной нитью, ).

Подставив выражение (2) в формулу (1) и учитывая, что , получим

Откуда искомая линейная плотность заряда нити

Ответ: τ = 4,33 мкКл/м.

Пример 12.5. Электростатическое поле создаётся в вакууме шаром радиусом R=8см, равномерно заряженными с объёмной плотностью ρ=10нКл/м³. Определите разность потенциалов между двумя точками этого поля, лежащими от центра шара на расстояниях: 1) r₁=10см и r₂=15см; 2) r₃= 2см и r₄=5см..

Дано: R=8см=8∙10^-2м; ρ=10нКл/м³=10∙10^-9нКл/м³; r₁=10см=10∙10^-2м;

r₂=15см=15∙10^-2м; r₃= 2см=2∙10^-2м; r₄=5см=5∙10^-2м.

Найти:1) φ₁- φ₂; 2) φ₃- φ₄.

Решение: 1) Разность потенциалов между двумя точками, лежащими на расстоянии r₁ и r₂ от центра шара.

(1)

где - напряжённость поля, создаваемого равномерно заряженным с объёмной плотностью ρ шаром, в любой точке, лежащей вне шара на расстоянии r от его центра.

Подставив это выражение в формулу (1) и проинтегрировав, получим искомую разность потенциалов

2) Разность потенциалов между двумя точками, лежащими на расстоянии r₃ и r₄ от центра шара,

(2)

где - напряжённость поля, создаваемого равномерно заряженным с объёмной плотностью ρ шаром, в любой точке, лежащей внутри шара на расстоянии r от его центра.

Подставив это выражение в формулу (2) и проинтегрировав, получим искомую разность потенциалов

Ответ: 1) φ₁- φ₂=0,643 В; 2) φ₃- φ₄=0,395 В