Идея аналитического решения ЗЛП

Ясно, что геометрический подход к решению ЗЛП годится только в случае, когда ОДР можно изобразить на плоскости. В общем случае такой подход не годится. В дальнейшем мы рассмотрим аналитический, так называемый симплекс-метод решения ЗЛП. А в этом разделе мы рассмотрим решение задачи, так сказать, «подручными» средствами, которые ярко демонстрируют идею симплекс-метода.

Решим наш предыдущий пример, одновременно проводя параллель с введёнными выше понятиями:

4x₁+x₂ ® max

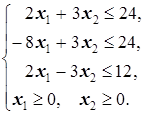
Приведём задачу к каноническому виду:

4x₁+x₂ ® max

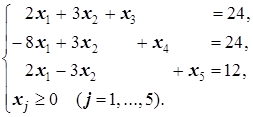
Так как определитель матрицы 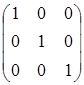, составленной из коэффициентов при переменных x₃, x₄, x₅ не равны нулю, то эти переменные - базисные, а переменные x₁ и x₂ - свободные. Положив x₁=x₂=0, получим базисное решение X₁=(0; 0; 24; 24; 12). Оно является допустимым: x_j≥0 при всех j=1, 2, …, 5. Оно также является базисным, и даже опорным. Число отличных от нуля координат этого решения равно r=3. Значит, оно является невырожденным. Базисом опорного решения являются векторы

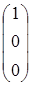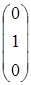A₃= , A₄= , A₅= .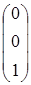

Согласно 3.1.4 любое опорное решение ЗЛП является угловой точкой ОДР, а согласно 3.1.2 целевая функция достигает экстремума в угловой точке. Поэтому мы можем проверить, не является ли это опорное решение решением задачи. Целевая функция в данном опорном решении принимает значение ноль. Коэффициенты целевой функции при свободных переменных положительны. Это означает, что стоит только начать менять хотя бы одну свободную переменную (так как x₁≥0 и x₂≥0, то они при изменении непременно принимают положительные значения), то значение функции сразу начнёт увеличиваться. Следовательно, опорное решение X₁ не является оптимальным, и переводом одной из свободных переменных x₁ или x₂ в базисные мы добьёмся увеличения значения целевой функции.

Мы заинтересованы не только в росте значения целевой функции, но и в том, чтобы этот рост происходил как можно быстрее. Поэтому будем менять (увеличивать) значение x₁, коэффициент при котором больше коэффициента при x₂. Другими словами, переведём x₁ из свободных в базисные.

В свою очередь, какая-то из базисных переменных должна перейти в число свободных. Какая?

Для того, чтобы определить, какая, выразим в системе ограничений-уравнений базисные переменные через свободные:

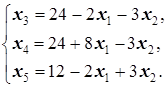
Из первого выражения ( 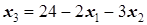) вытекает, что x₁ мы можем увеличивать до 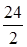=12. Как только x₁ станет больше 12, так сразу x₃<0, что недопустимо. Вообще, ясно, что x₁ мы можем менять (увеличивать) до min 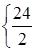, , 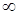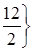=6 (здесь 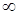означает, что во втором выражении x₁ можем увеличивать сколько угодно, и x₄ будет оставаться больше 0). Как только x₁=6, так сразу (при x₂=0) x₅=0. А это означает, что x₅ и x₁ примут значения в том опорном решении, где x₁, x₃, x₄ - базисные, а x₂ и x₅ - свободные. Поэтому x₁ переводим из свободных в базисные, а x₅ - из базисных в свободные. Поэтому из последнего выражения выразим x₁ через x₂ и x₅, и подставим его выражение в остальные и в целевую функцию:

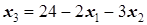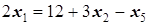Û Û .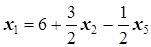

Теперь подставляем выражения для x₁ в выражение для x₃, x₄ и целевой функции:

= ,

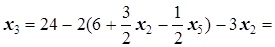
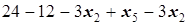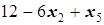то есть x₃= .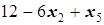

= ,

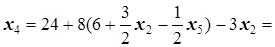
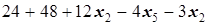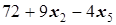то есть x₄= .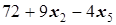

=

= ,

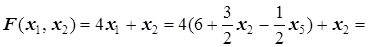
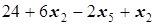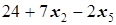то есть .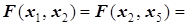

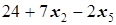Таким образом, наша задача принимает вид

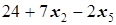® max

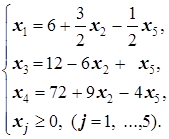
При x₂=x₅=0 получаем новое опорное решение (опорный план) X₂=(6; 0; 12; 72; 0), при котором F=24. Так как в 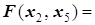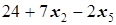коэффициент при x₂ положителен, то, меняя (то есть по сути увеличивая) x₂, добьёмся дальнейшего увеличения значения целевой функции 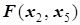. Поэтому переведём x₂ из свободных в базисные. Так как min 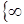, , 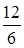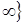=2 достигается в выражении для x₃, то x₂ вводим в число базисных вместо x₃. Выражаем x₃ через x₃, x₅ и подставляем его выражение в выражения для x₁, x₄ и в целевую функцию:

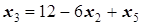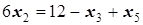Û Û .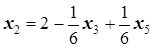

= ,

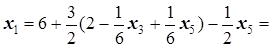
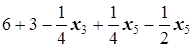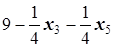то есть x₁= .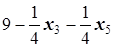

= ,

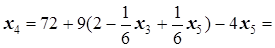
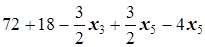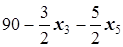то есть x₄= .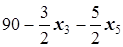

=

= ,

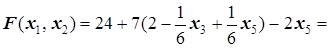
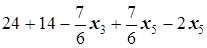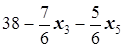то есть .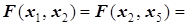

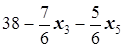Таким образом, наша задача принимает вид

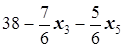® max

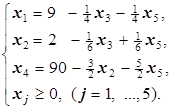
При x₃=x₅=0 получаем опорное решение X₂=(9; 2; 0; 90; 0), в котором целевая функция принимает значение F=38. Это значение уже увеличить невозможно, так как коэффициенты при переменных отрицательны, и любое изменение (увеличение) значений свободных переменных ведёт к уменьшению значения целевой функции.

Как видим, мы получили то же решение. что и в геометрическом методе.