Глава 3. Работа с графиками в MatLab

MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое.

Функция plot

Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах.

Предположим, что требуется вывести график функции синуса в диапазоне от 0 до . Для этого зададим вектор (множество) точек по оси Ox, в которых будут отображаться значения функции синуса:

x = 0:0.01:pi;

В результате получится вектор столбец со множеством значений от 0 до и с шагом 0,01. Затем, вычислим множество значений функции синуса в этих точках:

y = sin(x);

и выведем результат на экран

plot(x,y);

В результате получим график, представленный на рис. 3.1.

Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика.

Рис. 3.1. Отображение функции синуса с помощью функции plot().

Функцию plot() можно записать и с одним аргументом x или y:

plot(x);
plot(y);

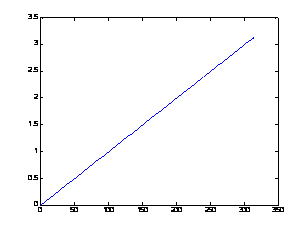
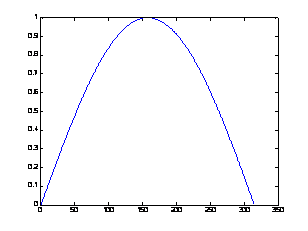
в результате получим два разных графика, представленные на рис. 3.2.

Анализ рис. 3.2 показывает, что в случае одного аргумента функция plot() отображает множество точек по оси Oy, а по оси Оx происходит автоматическая генерация множества точек с единичным шагом. Следовательно, для простой визуализации вектора в виде двумерного графика достаточно воспользоваться функцией plot() с одним аргументом.

Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом:

x = 0:0.01:pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2);

Результат работы данного фрагмента программы представлен на рис. 3.3.

а) б)

Рис. 3.2. Результаты работы функции plot() с одним аргументом:

а – plot(x); б – plot(y).

Рис. 3.3. Отображение двух графиков в одних координатных осях.

Аналогичным образом можно построить два графика, используя один аргумент функции plot(). Предположим, что есть два вектора значений

y1 = sin(x);
y2 = cos(x);

которые требуется отобразить на экране. Для этого объединим их в двумерную матрицу

в которой столбцы составлены из векторов y1 и y2 соответственно. Такая матрица будет отображена функцией

plot([y1’ y2’]); % апострофы переводят вектор-строку
% в вектор-столбец

в виде двух графиков (рис. 3.4).

Рис. 3.4. Отображение двумерной матрицы в виде двух графиков.

Два вектора в одних осях можно отобразить только в том случае, если их размерности совпадают. Когда же выполняется работа с векторами разных размерностей, то они либо должны быть приведены друг к другу по числу элементов, либо отображены на разных графиках. Отобразить графики в разных координатных осях можно несколькими способами. В самом простом случае можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом:

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

plot(x1, y1); % рисование первого графика
figure; % создание 2-го графического окна
plot(x2, y2); % рисование 2-го графика во 2-м окне

Функция figure, используемая в данной программе, создает новое графическое окно и делает его активным. Функция plot(), вызываемая сразу после функции figure, отобразит график в текущем активном графическом окне. В результате на экране будут показаны два окна с двумя графиками.

Неудобство работы приведенного фрагмента программы заключается в том, что повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. В этом случае было бы лучше построить программу так, чтобы на экране всегда отображалось два окна с нужными графиками. Этого можно достичь, если при вызове функции figure в качестве аргумента указывать номер графического окна, которое необходимо создать или сделать активным, если оно уже создано. Таким образом, вышеприведенную программу можно записать так.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1); %создание окна с номером 1
plot(x1, y1); % рисование первого графика
figure(2); % создание графического окна с номером 2
plot(x2, y2); % рисование 2-го графика во 2-м окне

При выполнении данной программы на экране всегда будут отображены только два графических окна с номерами 1 и 2, и в них показаны графики функций синуса и косинуса соответственно.

В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис:

subplot(<число строк>, <число столбцов>, <номер координатной оси>)

Рассмотрим пример отображения двух графиков друг под другом вышеприведенных функций синуса и косинуса.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1);
subplot(2,1,1); % делим окно на 2 строки и один столбец
plot(x1,y1); % отображение первого графика
subplot(2,1,2); % строим 2-ю координатную ось
plot(x2,y2); % отображаем 2-й график в новых осях

Результат работы программы показан на рис. 3.5.

Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Для этого используется параметр position в функции subplot():

subplot(‘position’, [left bottom width height]);

где left – смещение от левой стороны окна; bottom – смещение от нижней стороны окна; width, height – ширина и высота графика в окне. Все эти переменные изменяются в пределах от 0 до 1.

Рис. 3.5. Пример работы функции subplot.

Ниже представлен фрагмент программы отображения графика функции синуса в центре графического окна. Результат работы показан на рис. 3.6.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

subplot(‘position’, [0.33 0.33 0.33 0.33]);
plot(x1,y1);

В данном примере функция subplot() смещает график на треть от левой и нижней границ окна и рисует график с шириной и высотой в треть графического окна. В результате, получается эффект рисования функции синуса по центру основного окна.

Таким образом, используя параметр position можно произвольно размещать графические элементы в плоскости окна.

Рис. 3.6. Пример работы функции subplot с параметром position.

Оформление графиков

Пакет MatLab позволяет отображать графики с разным цветом и типом линий, показывать или скрывать сетку на графике, выполнять подпись осей и графика в целом, создавать легенду и многое другое. В данном параграфе рассмотрим наиболее важные функции, позволяющие делать такие оформления на примере двумерных графиков.

Функция plot() позволяет менять цвет и тип отображаемой линии. Для этого, используются дополнительные параметры, которые записываются следующим образом:

plot(<x>, <y>, <’цвет линии, тип линии, маркер точек’>);

Обратите внимание, что третий параметр записывается в апострофах и имеет обозначения, приведенные в таблицах 3.1-3.3. Маркеры, указанные ниже записываются подряд друг за другом, например,

‘ko’ – на графике отображает черными кружками точки графика,
‘ko-‘ – рисует график черной линией и проставляет точки в виде кружков.

Табл. 3.1. Обозначение цвета линии графика

Маркер	Цвет линии
c	голубой
m	фиолетовый
y	желтый
r	красный
g	зеленый
b	синий
w	белый
k	черный

Табл. 3.2. Обозначение типа линии графика

Маркер	Цвет линии
-	непрерывная
--	штриховая
:	пунктирная
-.	штрих-пунктирная

Табл. 3.3. Обозначение типа точек графика

Маркер	Цвет линии
.	точка
+	плюс
*	звездочка
o	кружок
x	крестик

Ниже показаны примеры записи функции plot() с разным набором маркеров.

x = 0:0.1:2*pi;
y = sin(x);

subplot(2,2,1); plot(x,y,'r-');
subplot(2,2,2); plot(x,y,'r-',x,y,'ko');
subplot(2,2,3); plot(y,'b--');
subplot(2,2,4); plot(y,'b--+');

Результат работы фрагмента программы приведен на рис. 3.7. Представленный пример показывает, каким образом можно комбинировать маркеры для достижения требуемого результата. А на рис. 3.7 наглядно видно к каким визуальным эффектам приводят разные маркеры, используемые в программе. Следует особо отметить, что в четвертой строчке программы по сути отображаются два графика: первый рисуется красным цветом и непрерывной линией, а второй черными кружками заданных точек графика. Остальные варианты записи маркеров очевидны.

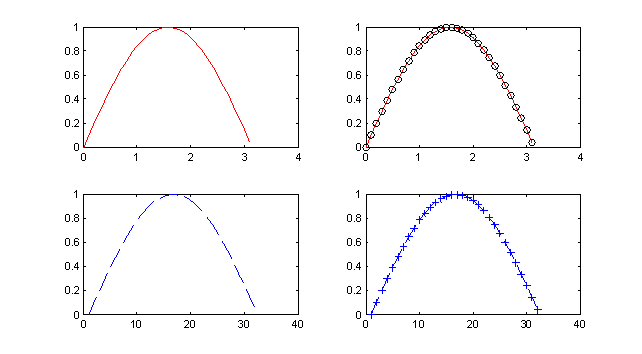
Рис. 3.7. Примеры отображения графиков с разными типами маркеров

Из примеров рис. 3.7 видно, что масштаб графиков по оси Ox несколько больше реальных значений. Дело в том, что система MatLab автоматически масштабирует систему координат для полного представления данных. Однако такая автоматическая настройка не всегда может удовлетворять интересам пользователя. Иногда требуется выделить отдельный фрагмент графика и только его показать целиком. Для этого используется функция axis() языка MatLab, которая имеет следующий синтаксис:

axis( [ xmin, xmax, ymin, ymax ] ),

где название указанных параметров говорят сами за себя.

Воспользуемся данной функцией для отображения графика функции синуса в пределах от 0 до :

x = 0:0.1:2*pi;
y = sin(x);

subplot(1,2,1);
plot(x,y);
axis([0 2*pi -1 1]);

subplot(1,2,2);
plot(x,y);
axis([0 pi 0 1]);

Из результата работы программы (рис. 3.8) видно, что несмотря на то, что функция синуса задана в диапазоне от 0 до , с помощью функции axis() можно отобразить как весь график, так и его фрагмент в пределах от 0 до .

Рис. 3.8. Пример работы функции axis()

В заключении данного параграфа рассмотрим возможности создания подписей графиков, осей и отображения сетки на графике. Для этого используются функции языка MatLab, перечисленные в табл. 3.4.

 

Таблица 3.4. Функции оформления графиков

Название	Описание
grid [on, off]	Включает/выключает сетку на графике
title(‘заголовок графика’)	Создает надпись заголовка графика
xlabel(‘подпись оси Ox’)	Создает подпись оси Ox
ylabel(‘подпись оси Oy’)	Создает подпись оси Oy
text(x,y,’текст’)	Создает текстовую надпись в координатах (x,y).

Рассмотрим работу данных функций в следующем примере:

x = 0:0.1:2*pi;
y = sin(x);

plot(x,y);
axis([0 2*pi -1 1]);
grid on;
title('The graphic of sin(x) function');
xlabel('The coordinate of Ox');
ylabel('The coordinate of Oy');
text(3.05,0.16,'\leftarrow sin(x)');

Из результата работы данной программы, представленного на рис. 3.9, видно каким образом работают функции создания подписей на графике, а также отображение сетки графика.

Таким образом, используя описанный набор функций и параметров, можно достичь желаемого способа оформления графиков в системе MatLab.

Рис. 3.9. Пример работы функций оформления графика