 |
Главная |
Пункт 2. Понятие графа
|
из
5.00
|
РАЗДЕЛ3. ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ, ТЕОРИИ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
ТЕМА 3.1. ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ.
План:
Множества и отношения между ними.
Понятие графа.
Пункт 1. Множества и отношения между ними.
Понятие множества.
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий. Опр.3.1. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называют элементами. Элементы множества отличают друг от друга. Например, множество всех книг в библиотеке или множество вершин многоугольника.
Множества обозначаются большими буквами. Например, A, B, C, X, N и т.д. Если объект a является элементом множества A, то говорят, что a принадлежит A. Это записывается, как 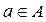 . Запись
. Запись 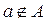 будет означать, что a не является элементом A.
будет означать, что a не является элементом A.
Множества как объекты могут быть элементами других множеств.
Опр.3.2. Множества, элементами которых являются другие множества, называются классом или семейством.
Опр.3.3. Множество, не содержащее элементов, называется пустым и обозначается 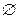 .
.
Задание множеств.
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать разными способами:
· перечислением М элементов: 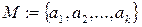 ;
;
· характеристическим свойством: 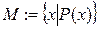 ;
;
Перечисление задается в фигурных скобках, через запятую.
Здесь и далее фигурными скобками 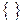 будем обозначать множество, в котором не играет роли порядок следования элементов, и круглыми скобками
будем обозначать множество, в котором не играет роли порядок следования элементов, и круглыми скобками 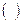 последовательность, в которой порядок следования элементов важен.
последовательность, в которой порядок следования элементов важен.
Пример 3.1.
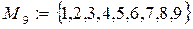 .
.
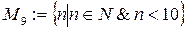 .
.
Операции над множествами
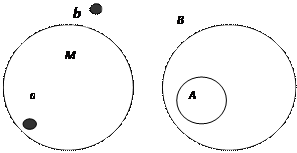
Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Элементы множества изображаются точками внутри круга, если они принадлежат множеству ( 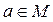 на рис 3.1 а), и точками вне круга, если они множеству не принадлежат (
на рис 3.1 а), и точками вне круга, если они множеству не принадлежат ( 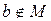 ).
).
|
|
Рис. 3.1. Иллюстрация кругами Эйлера
Будем также использовать символы 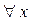 вместо слов «для любых х», «каждый элемент х» и
вместо слов «для любых х», «каждый элемент х» и 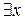 вместо слов «существует х».
вместо слов «существует х».
Сравнение множеств.
Опр.3.4. Множество A содержится во множестве B (множество B включает в себя множество A), если каждый элемент A принадлежит также и B (рис 1.1 б):
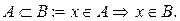
В этом случае A называется подмножеством B, а B – надмножеством A.
Опр.3.5. Если 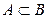 и
и 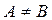 , то A называется собственным подмножеством B.
, то A называется собственным подмножеством B.
Опр.3.6. Два множества равны, если они являются подмножествами друг друга, т.е. 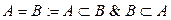 .
.
Мощность множества обозначается как |М|. Для конечных множеств мощность – это число элементов. Например, 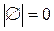 , но
, но 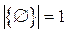 .
.
Опр.3.7. Если А=В, то множества A и B называются равномощными.
Пример 3.2.
Множество решений (корней) уравнения 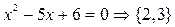 , т.е.
, т.е. 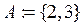 . Множество простых чисел, меньших пяти
. Множество простых чисел, меньших пяти 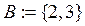 . Следовательно, А=В.
. Следовательно, А=В.
Опр.3.8. Если в множестве A найдется хотя бы один элемент, не принадлежащий B, то A не является подмножеством B, т.е. 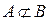 .
.
Пример 3.3.
Интервал 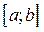 не является подмножеством промежутка
не является подмножеством промежутка 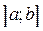 , так как
, так как 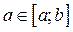 , но
, но 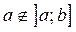 .
.
Из определения следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение 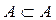 . Полагают, что Æ является подмножеством любого множества.
. Полагают, что Æ является подмножеством любого множества.
Пример 3.4.
Рассмотрим множество, состоящее из трех элементов: 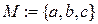 . Найдем все его подмножества:
. Найдем все его подмножества:
а) пустое 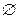 ;
;
б) по одному 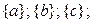
в) по два 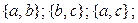
г) по три 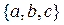 .
.
Число всех подмножеств составляет 8=23. Если множество состоит из n элементов, то число всех подмножеств равно 2n. Или булеан |2М|=2|М|.
Пересечение множеств.
Опр.3.9. Множество, состоящее из всех элементов, принадлежащих и множеству A, и множеству B, называется пересечением и обозначается 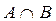 .
.
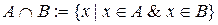 .
.
Пример 3.5.
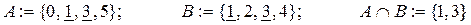 .
.
Если же множества A и B не имеют общих элементов, то их пересечением является пустое множество, то есть 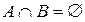 . Например, пересечение множества четных чисел с множеством нечетных.
. Например, пересечение множества четных чисел с множеством нечетных.
Пересечение пустого множества с любым множеством – пустое множество: 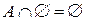 .
.
Свойства пересечения
1. Коммутативность (переместительное свойство). 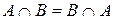 .
.
2. Ассоциативность. 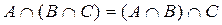 .
.
3. Свойство нуля. 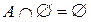 .
.
4. Идемпотентность 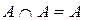 .
.
5. Дистрибутивность.
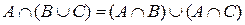 ;
; 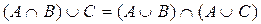
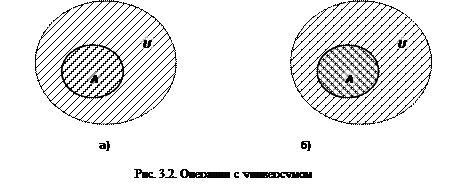
6. Свойство единицы. Если задан универсум U и любые 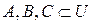 , то можно записать:
, то можно записать: 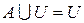 (рис. 3.2 а);
(рис. 3.2 а); 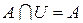 (рис. 3.2 б).
(рис. 3.2 б).
Объединение множеств.
Опр.3.10. Множество, состоящее из всех элементов, принадлежащих или множеству A, или множеству B, называется объединением множеств. Обозначается так: 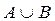 .
.
Пример 3.6.
Даны множества 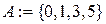 и
и 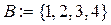 . Их объединением будет
. Их объединением будет 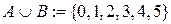 .
.
Пример 3.7.
Даны числовые промежутки (рис. 3.3). Их объединением будет 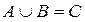 .
.
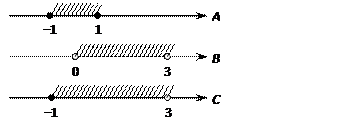
Рис. 3.3. Множества точек отрезков
Объединение и пересечение множеств хорошо иллюстрируются на плоскости (рис. 3.4). При этом множества изображаются кругами или прямоугольниками.
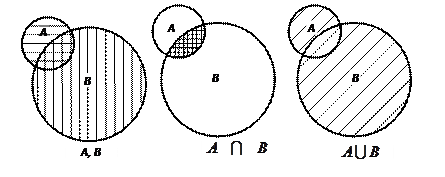
Рис. 3.4. Операции над множествами
Свойства объединения
1. Коммутативность 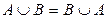 .
.
2. Ассоциативность. 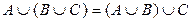 .
.
3. Свойство нуля. 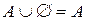 .
.
4. Идемпотентность 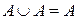 .
.
5. Дистрибутивность. 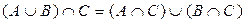 .
.
Разность множеств.
Записывается так: 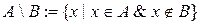 .
.
Геометрическое представление разности множеств на рис. 3.5.
Симметричная разность
Геометрическая интерпретация симметрической разности множеств представлена на рис. 3.6.
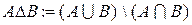 ;
;
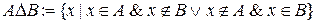 .
.

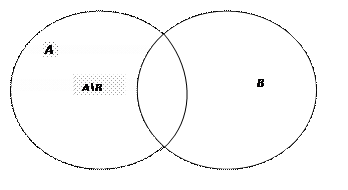
Рис. 3.5. Разность множеств Рис. 3.6. Симметричная разность
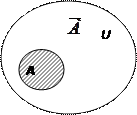 Дополнение множеств
Дополнение множеств
Геометрическое представление
дополнения множеств представлена на рис.рис. 3.7.
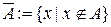 ;
;
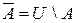 . Рис. 3.7. Дополнение множеств
. Рис. 3.7. Дополнение множеств
Свойства дополнения
 :
:
1) 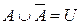 ; 3)
; 3) 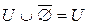 ; 5)
; 5) 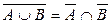 ;
;
2) 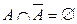 ; 4)
; 4) 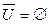 ; 6)
; 6) 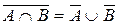 .
.
Пример 3.8.
Рассмотрим операцию дополнения множества, являющегося пересечением множеств A и B. Её результат совпадает с объединением дополнений этих множеств, (свойство 6) 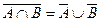 ; в этом можно убедиться с помощью диаграмм Эйлера – Венна (рис. 3.8).
; в этом можно убедиться с помощью диаграмм Эйлера – Венна (рис. 3.8).
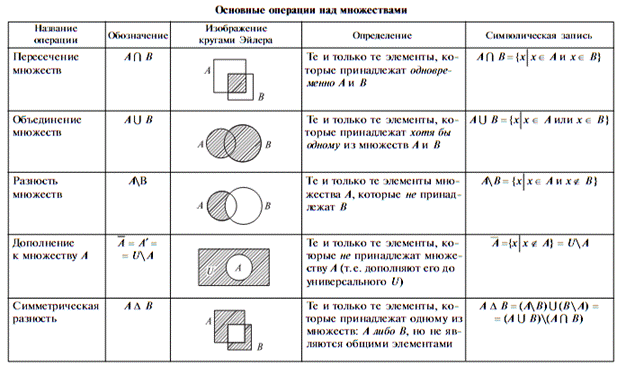
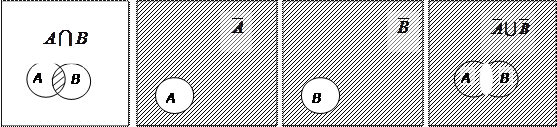
Рис. 3.8. Геометрическая иллюстрация свойства 6
Все основные операции над множествами можно записать в одну таблицу.
Пункт 2. Понятие графа.
Понятие графа.
Понятие графа опирается на основные понятия теории множеств, так как граф можно рассматривать как объект, состоящий из двух множеств - множества точек (вершин) X и множества линий (рёбер) U, которые соединяют некоторые вершины. При этом совершенно несущественно, соединены ли вершины графа отрезками прямых линий или криволинейными дугами, какова длина линий, как расположены вершины графа на плоскости и другие геометрические характеристики графа. Каждое ребро представляет собой неупорядоченную пару вершин из множества X.
Опр.3.11. Графом называется объект, состоящий из множества точек (вершин) X и множества линий (рёбер) U, которые соединяют некоторые вершины.
Математическая запись графа включает обозначения множеств вершин и рёбер, например, G = (X, U),где X - множество вершин; U - множество рёбер.
Пример изображения графа G, состоящего из множества вершин X = {x1, x2, x3, x4, x5} и множества рёбер U = {u12, u13, u14, u15, u24, u25, u35} представлен на рис. 3. 9.
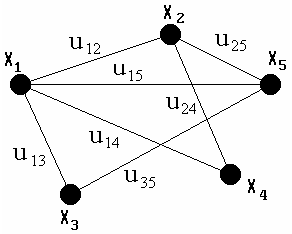
Рис. 3.9. Граф, состоящий из множества вершин Х и множества ребер U.
Элементы множеств X и U могут содержать индексы. Индексы вершин обозначают их номера. Индексы рёбер обозначают номера соединяемых ими вершин. Запись uij означает, что ребро графа образовано парой вершин xi и xj:
uij = (xi, xj), xi є X, xj є X.
Виды графов.
Опр.3.12.Конечный граф - это граф G = (X, U), у которого количество его вершин |X| конечно. Конечный граф представлен на рис. 3.9.
Опр.3.13. Нуль-граф - это граф G = (X, U), состоящий только из изолированных вершин, т.е. граф, не содержащий ни одного ребра (|U| = 0). Такой граф обозначается G0.
Нуль-граф, у которого |X| = 5 и |U| = 0 представлен на рис. 3.9.
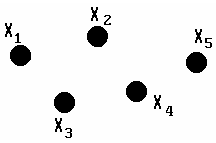
Рис. 3.9. Нуль-граф с пятью вершинами.
Опр.3.14. Пустой граф - это граф G = (X, U), не содержащий ни вершин, ни рёбер (|X| =0, |U| = 0). Такой граф обозначается Gø.
Опр.3.15. Неориентированный граф (неограф) - это граф G = (X, U), для каждого рёбра которого несуществен порядок двух его концевых вершин.
Неограф представлен на рис. 3.8. Рёбра неографа иногда называют звеньями.
Опр.3.16. Ориентированный граф (орграф) - это граф, для каждого ребра которого существен порядок двух его концевых вершин.
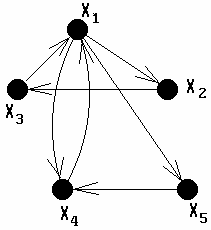
Орграф представлен на рис. 3.10 и обозначается 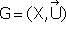 . Рёбра орграфа иногда называют дугами.
. Рёбра орграфа иногда называют дугами.
| 
|
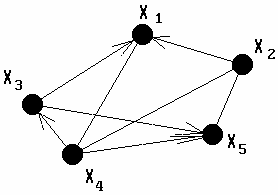
| Рис. 3.10. Орграф. | Рис. 3.11. Смешанный граф. |
Опр.3.17. Смешанный граф - это граф, который содержит как ориентированные, так и неориентированные рёбра. Смешанный граф обозначается 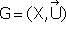 .
.
Смешанный граф представлен на рис. 3.11.
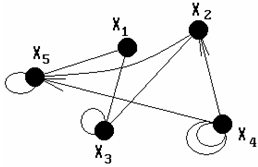
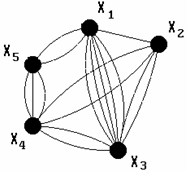
Любой из перечисленных видов графа может содержать одно или несколько рёбер, у которых оба конца сходятся в одной вершине, т.е. uij є U, uij = (xi, xj), i = j. Такие рёбра называются петлями. На рис. 3.12 представлен смешанный граф с петлями.
| 
|
| Рис. 3.12. Смешанный граф с петлями. | Рис. 3.13. Мультиграф. |
В общем случае множество рёбер U может состоять из трёх непересекающихся подмножеств: подмножества звеньев, подмножества дуг и подмножества петель.
Ребро uij, соединяющее вершины xi и xj, инцидентно данным вершинам и наоборот, вершины xi и xj инцидентны ребру uij. Ребро u12 (рис. 3.13) инцидентно вершинам x1 и x2, а вершины x1 и x2, в свою очередь, инцидентны ребру u12.
Опр.3.18. Мультиграф (рис. 3.13) - это граф, у которого любые две вершины соединены более чем одним ребром.
Опр.3.19. Рёбра, соединяющие одну и ту же пару вершин, называются кратными.
Опр.3.20. Наибольшее число кратных рёбер, соединяющих какую-либо пару вершин, называется мультичислом.
Мультичисло графа, представленного на рис. 3.13, m = 5.
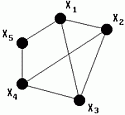
Опр.3.21. Скелет мультиграфа - это граф, полученный из исходного мультиграфа путём удаления петель и сведения кратных рёбер в одно ребро.
На рис. 3.14 показан скелет мультиграфа, представленного на рис. 3.13.
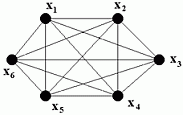
Опр.3.22. Полный граф (рис. 3.15.) - это граф, у которого любые две вершины соединены ребром. Полный граф обозначается Gп.
| 
| 
|
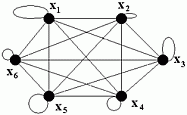
| Рис. 3.14. Скелет мультиграфа. | Рис. 3.15. Полный граф. | Рис. 3.16. Плотный граф. |
Опр.3.23. Плотный граф (рис. 3.16.) - это полный граф, у которого при каждой вершине имеется петля. Плотный граф обозначается G′п.
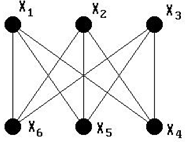
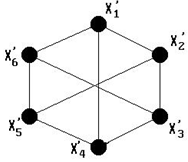
Опр.3.24. Изоморфные графы - это два графа G = (X, U) и G′ = (X′, U′), у которых можно установить взаимно однозначное соответствие X ↔ X′, U ↔ U′, такое, что, если xi, xj є X соответствует x′i, x′j є X′ то ребро uij є U соответствует ребру ребро u′ij є U′.
На рис. 3.17 и 3.18 показаны изоморфные графы G1 и G2, у которых вершинам x1, x2, x3, x4, x5, x6 поставлены во взаимно однозначное соответствие вершины x′1, x′2, x′3, x′4, x′5, x′6.
| 
|
| Рис. 3.17. | Рис. 3.18. |
Опр.3.25. Плоский граф - это граф G = (X, U), у которого рёбра расположены на плоскости таким образом, что пересекаются только в вершинах.
Опр.3.26.Планарный граф - это граф G = (X, U), изоморфный плоскому графу.
Опр.3.27. Смежными вершинами называются любые две вершины xi, xj є X графа G = (X, U), инцидентные одному и тому же ребру.
Так, например, вершины xi и xj (рис. 3.1) являются смежными, а вершины x4 и x5 смежными не являются, так как не соединены между собой, т.е. ребро u45 отсутствует.
Опр.3.28. Локальной степенью (или просто степенью) вершины xi графа G = (X, U) называется количество рёбер ρ(xi), инцидентных данной вершине.
Сумма локальных степеней 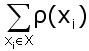 всех вершин графа G = (X, U) есть удвоенное количество всех его рёбер:
всех вершин графа G = (X, U) есть удвоенное количество всех его рёбер:
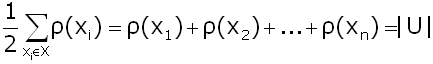
Поскольку для полного графа ρ(x1) = ρ(x2) = ... = ρ(xn) = n - 1, то в этом случае
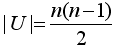 .
.
Опр.3.29. Граф называется однородным степени t, если локальные степени всех его вершин равны между собой, т.е. ρ(x1) = ρ(x2) = ... = ρ(xn) = t.
Количество рёбер однородного графа степени t равно
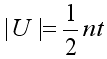 .
.
Связность графов.
Пусть задан неограф G = (X, U) без петель и кратных рёбер.
Опр.3.30. Маршрут - это последовательность рёбер ui є U, заданных парами вершин вида (x1, x2) (x2, x3) ... (xi-1, xi), в которой любые два соседних ребра смежные. Количество рёбер в маршруте определяет его длину.
Опр.3.31. Если все рёбра в маршруте различны, то такой маршрут является цепью.
Опр.3.32. Если в цепи нет повторяющихся вершин, кроме соседних, то такая цепь называется простой.
Опр.3.33. Цепь, в которой совпадают начальная и конечная вершины, называется циклом.
Опр.3.34. Простая цепь, в которой совпадают начальная и конечная вершины, образует простой цикл.
Граф, представленный на рис. 3.1, содержит, например,
маршрут: (x1, x3) (x3, x5) (x5, x2) (x2, x4) (x4, x1);
простую цепь (x1, x3) (x3, x5) (x5, x2) (x2, x4);
простой цикл (x1, x3) (x3, x5) (x5, x2) (x2, x1).
Опр.3.35. Две вершины xi, xj є X, xi ≠ xj графа G = (X, U) называются связанными, если их можно соединить маршрутом.
Опр.3.36. Граф G = (X, U) называется связным, если любые две его вершины связаны маршрутом.
Если взять какую-либо вершину xi є X графа G = (X, U) и построить подмножество X′ 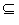 X, состоящее из всех вершин, которые можно соединить с вершиной xi произвольным маршрутом, причём xi включается в множество X′, то подграф G′ = (X′, U′), образованный на множестве вершин X′, называется компонентой связности графа G.
X, состоящее из всех вершин, которые можно соединить с вершиной xi произвольным маршрутом, причём xi включается в множество X′, то подграф G′ = (X′, U′), образованный на множестве вершин X′, называется компонентой связности графа G.
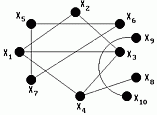
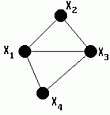
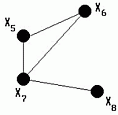
Связный граф состоит из единственной компоненты связности. Если граф имеет несколько компонент связности, то он несвязен, так как вершины из разных компонент связности нельзя соединить маршрутом. На рис. 3.19 показан граф G = (X, U), состоящий из трёх компонент связности G1, G2 и G3, представленных на рис. 3.20-3.22.
| 
| 
| 
|
| Рис. 3.19. Граф, состоящий из трех компонентов связности. | Рис. 3.20. Первая компонента связности | Рис. 3.21. Вторая компонента связности. | Рис. 3.22. третья компонента связности. |
Опр.3.37. Связный граф без циклов называется деревом.
В дереве любые две вершины связаны единственной цепью. Пример дерева показан на рис. 3.23.
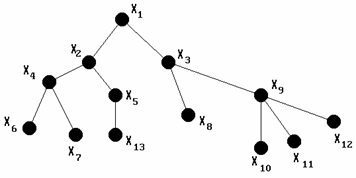
Рис. 3.23. Изображение дерева.
Общее количество деревьев d, которое можно построить на n вершинах, определяется по формуле (теорема Кэли) d = nn-2.
Опр.3.38. Цикл Cэ, в котором содержатся все рёбра графа, причём каждое ребро встречается только один раз, называется эйлеровым.
Граф содержит Эйлеров цикл, если он связен и все локальные степени его вершин чётны.
Опр.3.39. Цикл Cг, проходящий через каждую вершину графа по одному разу, называется гамильтоновым.
Для гамильтонова цикла, в отличие от эйлерова цикла, неизвестен общий критерий существования. В литературе можно встретить только частные критерии, например, согласно одному из критериев в графе существует гамильтонов цикл, если для любой пары вершин xi, xj є X графа G сумма локальных степеней ρ(xi) + ρ(xj) ≥ n.
Пример 3.9.
В государстве 100 городов, из каждого выходит 2 дороги, кроме столицы, откуда выходит 5 дорог и города Горный, откуда выходит одна единственная дорога. Сколько всего дорог в государстве?
Решение: Сложим количества дорог, выходящих из всех городов: 98*2+5+1=202. Это число - количество концов всех дорог. Поскольку каждая дорога имеет 2 конца, то количество дорог будет вдвое меньше, а именно 101.
Пример 3.10.
На остров Коневец завезли 13 телефонов. Настоятель хочет организовать такую схему телефонной связи, чтобы соединить каждый телефон ровно с 7-ю другими. Удастся ли ему это?
Решение: Посчитаем, сколько проводов нужно, чтобы осуществить такую схему. Концов проводов будет 13*7=91, а самих проводов - вдвое меньше, то есть... 45,5 штук. Это означает, что такая схема связи невозможна.
Пример 3.11.
Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
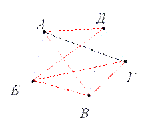 Решение. На рисунке 3.24. изображен граф, соответствующий всем совершенным рукопожатиям. Если подсчитать число ребер графа, изображенного на рисунке, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
Решение. На рисунке 3.24. изображен граф, соответствующий всем совершенным рукопожатиям. Если подсчитать число ребер графа, изображенного на рисунке, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
Пример 3.12.
 Доска имеет форму двойного креста, который получается, если из квадрата 4x4 убрать угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
Доска имеет форму двойного креста, который получается, если из квадрата 4x4 убрать угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
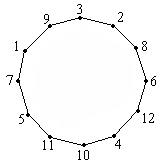
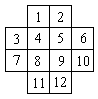 Решение: Занумеруем последовательно клетки доски.
Решение: Занумеруем последовательно клетки доски.
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен.
Пример 3.13.
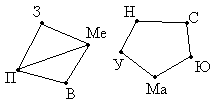 Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
По рисунку сразу видно, что долететь с Земли до Марса нельзя.
Пример 3.14.
В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
Пример 3.15.
Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.
Пример 3.16.



Пример 3.17.

|
из
5.00
|
Обсуждение в статье: Пункт 2. Понятие графа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

