Непрерывность функции. Классификация точек разрыва

2015-12-07

2204

Обсуждений (0)

0.00 из 5.00 0 оценок

Функция называется непрерывной в точке х₀, если:

1) функция f(x) определена в точке и некоторой её окрестности;

2) пределы слева и справа существуют и равны между собой: ;

3) .

Если в точке х₀ не выполняется хотя бы одно из условий, то эта точка х₀ называется точкой разрыва функции.

Для определения вида разрыва в точке х₀находят односторонние пределы и . При этом:

а) если существуют односторонние пределы , но , то говорят, что функция терпит в точке х₀разрыв типа выколотой точки. Разрыв типа выколотой точки называют устранимым. Чтобы его устранить, нужно доопределить функцию в точке х₀ либо изменить значение f(x) в точке х₀ таким образом, чтобы выполнялось ;

б) если существуют односторонние пределы 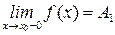и , но , то не существует; в этом случае говорят, что функция терпит в точке х₀разрыв типа«скачок». Разность называется скачком функции в точке х₀;

в) если левосторонний либо правосторонний (или оба) пределы функциипри бесконечные, то говорят, что функция терпит в точке бесконечный разрыв.

Разрывы типа выколотой точки и типа «скачок» относятся к конечным разрывам, или разрывам I рода, бесконечные разрывы относятся к разрывам II рода.

Функция f(х) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

Свойства непрерывных функций

1. Если функции f(x) и g(x) непрерывны в точке х₀, то их сумма также есть непрерывная функция в точке х₀. Это свойство справедливо для любого конечного количества слагаемых.

2. Произведение конечного количества непрерывных функций есть функция непрерывная.

3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

4. Сложная функция, составленная из непрерывных функций, непрерывна в соответствующей точке.

5. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

----------------------------------------------------------------------------------------------------------------

Непрерывность функции. Классификация точек разрыва. Стр.1

При отыскании точек разрыва функции можно руководствоваться следующими положениями:

а) элементарная функция может иметь разрыв только в той точке, где она неопределена, при условии, что она определена хотя бы с одной стороны от той точки в сколь угодно близких к ней точках;

б) неэлементарная функция может иметь разрывы как в точках, в которых она неопределена, так и в точках, где она определена; в частности, если функция задана несколькими различными формулами для различнх интервалов изменения аргумента, то она может иметь разрывы в тех точках, где меняется её аналитическое выражение (формула).

2015-12-07 2204 Обсуждений (0)

0.00 из 5.00 0 оценок

Обсуждение в статье: Непрерывность функции. Классификация точек разрыва

Обсуждений еще не было, будьте первым... ↓↓↓

Имя *

Email (необязательно)

Комментарий *

Отправить сообщение

Популярное:
Генезис конфликтологии как науки в древней Греции: Для уяснения предыстории конфликтологии существенное значение имеет обращение к античной...
Почему в черте города у деревьев заболеваемость больше, а продолжительность жизни меньше?
Почему наличие хронического атрофического гастрита способствует возникновению и развитию опухоли желудка?
Личность ребенка как объект и субъект в образовательной технологии: В настоящее время в России идет становление новой системы образования, ориентированного на вхождение...