 |
Главная |
Пример выполнения работы. Найти наименьший положительный корень уравнения
|
из
5.00
|
Найти наименьший положительный корень уравнения
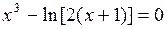 .
.
1. Область определения функции 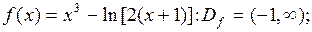 ее производные
ее производные
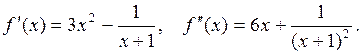
2. Строим графики функций: 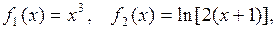 находим точки пересечения графиков. Из рис. 2.6 видно, что наименьший положительный корень данного уравнения лежит внутри отрезка
находим точки пересечения графиков. Из рис. 2.6 видно, что наименьший положительный корень данного уравнения лежит внутри отрезка 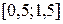 . Проверим аналитически, что корень отделен на этом отрезке. Вычисляем:
. Проверим аналитически, что корень отделен на этом отрезке. Вычисляем: 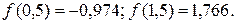 Поскольку
Поскольку 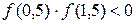 и функция непрерывна, то в силу теоремы 1 внутри отрезка
и функция непрерывна, то в силу теоремы 1 внутри отрезка 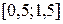 имеются корни. Поскольку
имеются корни. Поскольку 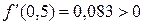 и
и 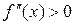 для всех
для всех 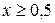 , следовательно
, следовательно 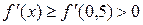 для всех
для всех 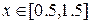 , т. е. функция возрастающая на
, т. е. функция возрастающая на 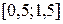 . Поэтому на основании теоремы 2 внутри этого отрезка имеется один корень уравнения и он может быть взят в качестве начального.
. Поэтому на основании теоремы 2 внутри этого отрезка имеется один корень уравнения и он может быть взят в качестве начального.
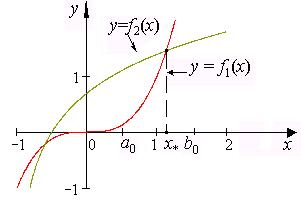
Рис. 2.6. Графики функций 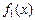 и
и 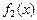
3. С помощью микрокалькулятора делаем 3 шага методом половинного деления; результаты заносим в табл. 2.2.
Таблица 2.2
Уточнение начального отрезка методом половинного деления
| N | 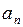
| 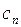
| 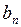
| 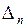
| 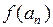
| 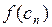
| 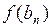
|
| 0,5 | 1,0 | 1,5 | 1,0 | – 0,974 | – 0,386 | 1,766 | |
| 1,0 | 1,25 | 1,5 | 0,5 | – 0,386 | 0,449 | 1,766 | |
| 1,0 | 1,125 | 1,25 | 0,25 | – 0,386 | – 0,023 | 0,449 | |
| 1,125 | 1,1875 | 1,25 | 0,125 |
В результате получаем: уточненный отрезок [1,125; 1,250]; приближенное значение корня 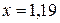 ; погрешность корня равной
; погрешность корня равной 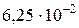 . При этом были введены следующие дополнительные обозначения:
. При этом были введены следующие дополнительные обозначения: 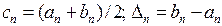 .
.
Дальнейшее уточнение корня проводим комбинированным методом. Так как 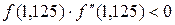 , то левый конец отрезка [1,125; 1,250] уточняем методом хорд, а правый – методом Ньютона. Поэтому используем формулы (2.13). Результаты вычислений заносим в табл. 2.3.
, то левый конец отрезка [1,125; 1,250] уточняем методом хорд, а правый – методом Ньютона. Поэтому используем формулы (2.13). Результаты вычислений заносим в табл. 2.3.
Таблица 2.3
Уточнение корня комбинированным методом
| N | 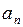
| 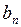
| 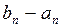
| 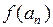
| 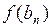
| 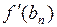
|
| 1,125 | 1,250 | 0,125 | – 0,023092 | 0,444045 | 4,243056 | |
| 1,131114 | 1,144170 | 0,013056 | – 0,002622 | 0,041961 | 3,460994 | |
| 1,131882 | 1,132046 | 0,000164 |
Так как 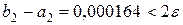 , вычисления прекращаем на втором шаге. Находим корень уравнения
, вычисления прекращаем на втором шаге. Находим корень уравнения
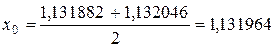
4. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab2.mcd. Вводим функцию
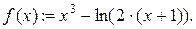
Строим график функции на найденном начальном интервале [0,5;1,5] (рис. 2.7)
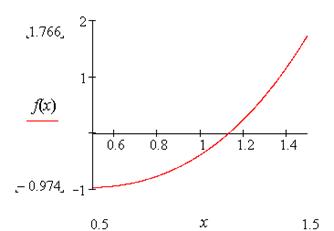
Рис. 2.7. График функции f(x)
Характеристики графика свидетельствуют, что функция непрерывна, 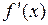 и
и 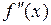 существуют и знакопостоянны на этом отрезке (т. е. функция монотонна и не меняет направление выпуклости) и что корень уравнения
существуют и знакопостоянны на этом отрезке (т. е. функция монотонна и не меняет направление выпуклости) и что корень уравнения 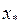 лежит в интервале [0,5;1,5], причем единственный. Таким образом, можем применить все вышеперечисленные методы. После этого находим корень с точностью до
лежит в интервале [0,5;1,5], причем единственный. Таким образом, можем применить все вышеперечисленные методы. После этого находим корень с точностью до 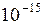 с помощью встроенной функции системы Mathcad
с помощью встроенной функции системы Mathcad
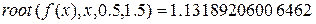
5. Выписываем точное решение 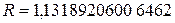 и сравниваем полученные результаты ручного и машинного счета. Определяем погрешность:
и сравниваем полученные результаты ручного и машинного счета. Определяем погрешность:
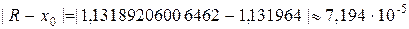
6. Определяем с помощью компьютера значение корня методом половинного деления с точностью 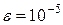 . По формуле, чтобы удовлетворить погрешности
. По формуле, чтобы удовлетворить погрешности 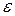 , для начального отрезка единичной длины необходимо провести
, для начального отрезка единичной длины необходимо провести 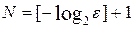 шагов.
шагов.
Выписываем автоматически вычисленное по этой формуле в соответствующем разделе количество шагов 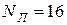 и таблицу 2.4, содержащую первые и последние три шага получившейся матрицы приближений корня методом половинного деления.
и таблицу 2.4, содержащую первые и последние три шага получившейся матрицы приближений корня методом половинного деления.
Таблица 2.4
Отыскание корня методом половинного деления
| N | … | |||||||
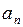
| 0,5 | 1,0 | 1,0 | 1,125 | … | 1,131836 | 1,131866 | 1,131882 |
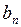
| 1,5 | 1,5 | 1,25 | 1,25 | … | 1,131897 | 1,131897 | 1,131897 |
Получим корень 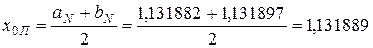 , абсолютная погрешность которого
, абсолютная погрешность которого 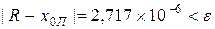 .
.
7. Получим на компьютере значение корня методом Ньютона с точностью 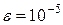 . Для этого вводим в начале соответсвующего раздела
. Для этого вводим в начале соответсвующего раздела 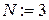 и с помощью запрограммированной формулы (2.7) определяем погрешность
и с помощью запрограммированной формулы (2.7) определяем погрешность 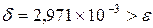 . Следовательно, увеличивая N на единицу, вводим в программу
. Следовательно, увеличивая N на единицу, вводим в программу 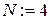 и получаем
и получаем 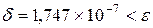 . То есть требуемая точность достигнута (если это не так продолжаем увеличивать N на единицу).
. То есть требуемая точность достигнута (если это не так продолжаем увеличивать N на единицу).
. Выписываем получившуюся таблицу 2.5 для 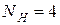 .
.
Таблица 2.5
Отыскание корня методом Ньютона
| N | |||||
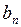
| 1,5 | 1,221958726 | 1,139300286 | 1,131948438 | 1,131892063 |
Получим приближенный корень 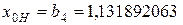 , абсолютная погрешность которого
, абсолютная погрешность которого 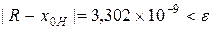 .
.
8. Вычисляем на компьютере значение корня методом хорд с точностью 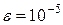 . Для этого вводим в начале соответсвующего раздела
. Для этого вводим в начале соответсвующего раздела 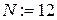 и с помощью запрограммированной формулы (2.10) получим и оценим погрешность
и с помощью запрограммированной формулы (2.10) получим и оценим погрешность 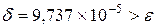 . Следовательно, увеличиваем N на единицу, вводим
. Следовательно, увеличиваем N на единицу, вводим 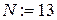 , для которого
, для которого 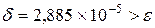 . Увеличиваем N еще на единицу, вводим
. Увеличиваем N еще на единицу, вводим 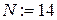 , для которого
, для которого 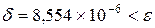 . Т. е. требуемая точность достигнута (если это не так, продолжаем увеличивать N на единицу).
. Т. е. требуемая точность достигнута (если это не так, продолжаем увеличивать N на единицу).
Выписываем первые и последние два шага из получившейся таблицы для 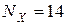 .
.
Таблица 2.6
Отыскание корня методом хорд
| N | … | |||||
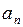
| 0,5 | 0,855440054 | 1,035664929 | … | 1,131891898 | 1,131892012 |
Получим корень 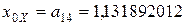 , абсолютная погрешность которого
, абсолютная погрешность которого 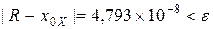 .
.
9. Вычисляем на компьютере значение корня комбинированным методом с точностью 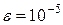 . Для этого вводим в начале соответсвующего раздела
. Для этого вводим в начале соответсвующего раздела 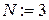 и получаем по формуле (2.13) погрешность
и получаем по формуле (2.13) погрешность 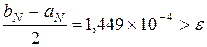 . Следовательно, увеличиваем N на единицу и вводим
. Следовательно, увеличиваем N на единицу и вводим 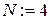 , для которого
, для которого 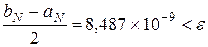 . То есть требуемая точность достигнута (если это не так, продолжаем увеличивать N на единицу).
. То есть требуемая точность достигнута (если это не так, продолжаем увеличивать N на единицу).
Выписываем получившуюся таблицу 2.7 для 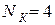 .
.
Таблица 2.7
Отыскание корня комбинированным методом
| N | |||||
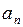
| 0,5 | 0,8554400542 | 1,1020813008 | 1,1316586589 | 1,1318920464 |
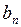
| 1,5 | 1,2219587264 | 1,1393002857 | 1,1319483820 | 1,1318920634 |
Получим корень 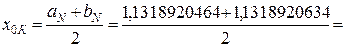
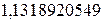 , абсолютная погрешность которого
, абсолютная погрешность которого 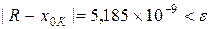 .
.
10. Все расчеты оформляются в виде отчета по лабораторной работе.
Вопросы для самоконтроля
1. Уравнение какого типа решается в данной работе?
2. Что называется корнем уравнения 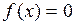 ?
?
3. Как графически решить уравнения 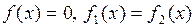 ?
?
4. Перечислите достоинства и недостатки графического метода.
5. В чем состоит этап отделения корней уравнения 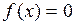 ?
?
6. Сколько корней должна иметь функция 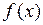 на начальном отрезке
на начальном отрезке 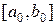 ?
?
7. Как определить аналитически: возрастает или убывает функция на промежутке?
8. Как определить аналитически: выпукла или вогнута функция на промежутке?
9. Какие условия, наложенные на 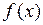 , гарантируют наличие хотя бы одного корня уравнения на начальном отрезке
, гарантируют наличие хотя бы одного корня уравнения на начальном отрезке 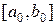 ?
?
10. Какие условия, наложенные на 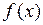 , гарантируют наличие не более одного корня уравнения на начальном отрезке
, гарантируют наличие не более одного корня уравнения на начальном отрезке 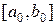 ?
?
11. Привести алгоритм решения уравнения 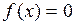 методом половинного деления. Какие условия при этом должны быть наложены на функцию
методом половинного деления. Какие условия при этом должны быть наложены на функцию 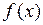 ?
?
12. Какие условия должны быть наложены на 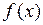 , чтобы уравнение можно было решить методом Ньютона?
, чтобы уравнение можно было решить методом Ньютона?
13. Как выбирается начальная точка 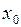 в методе Ньютона?
в методе Ньютона?
14. Вывести формулу для вычисления последовательных приближений методом Ньютона, записать формулу оценки погрешности.
15. Какие условия должны быть наложены на 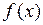 , чтобы уравнение
, чтобы уравнение 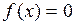 можно было решить методом хорд?
можно было решить методом хорд?
16. Как выбирается начальная точка 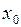 в методе хорд?
в методе хорд?
17. Вывести формулу для вычисления n последовательных приближений методом хорд, записать формулу оценки погрешности.
18. Какие условия должны быть наложены на 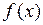 , чтобы уравнение
, чтобы уравнение 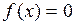 можно было решить комбинированным методом?
можно было решить комбинированным методом?
19. Выписать формулы, по которым уточняются концы начального отрезка 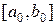 комбинированным методом. В зависимости от каких условий осуществляется выбор формул?
комбинированным методом. В зависимости от каких условий осуществляется выбор формул?
20. Указать условие, по которому процесс уточнения отрезка комбинированным методом должен быть прерван? Как затем найти корень?
|
из
5.00
|
Обсуждение в статье: Пример выполнения работы. Найти наименьший положительный корень уравнения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

