 |
Главная |
Теоретический материал к разделу
|
из
5.00
|
Решение типовых задач
Задача №1.Найти общий интеграл дифференциального уравнения
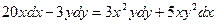
Решение: Данное уравнение перепишем в виде:
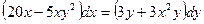 , далее
, далее  это дифференциальное уравнение ( в дальнейшем ДУ) первого порядка с разделяющимися переменными, т.е.
это дифференциальное уравнение ( в дальнейшем ДУ) первого порядка с разделяющимися переменными, т.е.

 или
или  .
.
Ответ:  - общий интеграл данного ДУ.
- общий интеграл данного ДУ.
Задача №2. Найти общий интеграл дифференциального уравнения 
Решение: Данное уравнение является ДУ первого порядка, однородным, т.к. его можно привести к виду  и
и  однородная функция нулевого измерения и, сделав замену переменных
однородная функция нулевого измерения и, сделав замену переменных  , привести к виду
, привести к виду 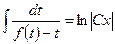 , далее вычисляя интеграл в левой части, найти ответ. У нас
, далее вычисляя интеграл в левой части, найти ответ. У нас 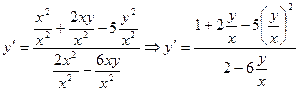
 ;
;  ;
;

 . Окончательно:
. Окончательно: 
Ответ:  - общий интеграл ДУ.
- общий интеграл ДУ.
Задача №3.Найти общий интеграл дифференциального уравнения  .
.
Решение: Данное ДУ первого порядка, приводящиеся к однородному. Сделаем замену переменных 
 , выбераем при этом
, выбераем при этом  так, чтобы
так, чтобы
 а уравнение примет вид:
а уравнение примет вид:
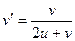 - однородное, первого порядка. Применим замену переменых
- однородное, первого порядка. Применим замену переменых 


 .
.
Из урвнений замены  , подставляя в общий интеграл ДУ получим:
, подставляя в общий интеграл ДУ получим: 
Ответ: 
Задача №4. Найти решение задачи Коши  ,
,  .
.
Решение: Данное ДУ является линейным неоднородным ДУ первого порядка. Решим его методом вариации произвольной постоянной. Сначала решим ДУ однородное, т.е.  . Это всегда ДУ с разделяющимися переменными
. Это всегда ДУ с разделяющимися переменными  - общие решение однородного линейного ДУ.
- общие решение однородного линейного ДУ.  в таком виде будем искать общее решение неоднородного ДУ, где
в таком виде будем искать общее решение неоднородного ДУ, где  - неизвестная функция,
- неизвестная функция, 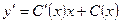 Подставляем
Подставляем  и у в исходное ДУ, будем иметь;
и у в исходное ДУ, будем иметь;
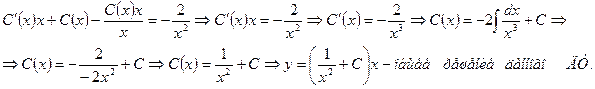
Найдем частное решение, используя начальные условия 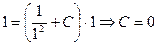 . Итак, задача Коши решена : найдено частное решение, ДУ, отвечающее начальному условию
. Итак, задача Коши решена : найдено частное решение, ДУ, отвечающее начальному условию 

Ответ: 
Задача №5.Найти общее решение дифференциального уравнения

Решение: Перепишем данное ДУ в виде  или
или  - это линейное ДУ первого порядка, неоднородное относительно
- это линейное ДУ первого порядка, неоднородное относительно  искомой функции , а
искомой функции , а  – независимая переменная. Решим его методом вариации произвольной постоянной. Сначала решаем однородное уравнение
– независимая переменная. Решим его методом вариации произвольной постоянной. Сначала решаем однородное уравнение 
 (
( 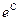 постоянная величина)
постоянная величина)  общее решение однородного уравнения. Общее решение неоднородного ищим в виде
общее решение однородного уравнения. Общее решение неоднородного ищим в виде  ,
,  . Подставим два последних выражения в неоднородное уравнение, получим:
. Подставим два последних выражения в неоднородное уравнение, получим:

Отдельно вычислим интеграл 
Преобразуем 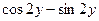 так :
так :

 . Тогда
. Тогда
 .Интегрируем далее по частям:
.Интегрируем далее по частям: 
Получили уравнение относительно искомого интеграла
 . Откуда
. Откуда 
Итак,  , преобразуем
, преобразуем
 Наконец,
Наконец,  .
.
Следовательно, общее решение исходного ДУ будет иметь вид:  или
или 
Ответ : 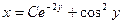
Задача №6. Найти решение задачи Коши  ,
, 
Решение:Перепишем данное ДУ в виде  это уравнение Бернулли. Решаем методом Бернулли:
это уравнение Бернулли. Решаем методом Бернулли: 

Решим задачу Коши: 
Ответ: 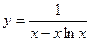 - частное решение исходного ДУ, удовлетворяющего начальному условию
- частное решение исходного ДУ, удовлетворяющего начальному условию 
Задача №7.Найти общий итеграл дифференциального уравнения

Решение: Данное ДУ перепишем в виде 
Проверим, является ли это ДУ в полных дифференциалах. У нас  ;
;  ;
;  ;
;  ; так как
; так как 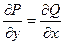 данное ДУ является ДУ первого порядка, в полных дифференциалах, т.е. имеет вид
данное ДУ является ДУ первого порядка, в полных дифференциалах, т.е. имеет вид  ,откуда
,откуда  общий интеграл исходного ДУ. Остается найти функцию
общий интеграл исходного ДУ. Остается найти функцию  , чей полный дифференциал стоит в левой части уравнения и
, чей полный дифференциал стоит в левой части уравнения и  ,
,  ;
; 
 с другой стороны,
с другой стороны,  значит ,
значит , 

 . Наконец,
. Наконец,  –
– 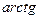
 и общий интеграл имеет вид
и общий интеграл имеет вид  –
– 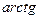
 , окончательно
, окончательно  ,
, 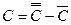 .
.
Ответ: общий интеграл 
Задача №8. Найти общее решение дифференциального уравнения
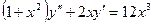
Решение: Данное ДУ второго порядка не содержит искомой функций  , значит, замена переменных такова:
, значит, замена переменных такова:  , откуда уравнение принимает вид:
, откуда уравнение принимает вид:  или
или  , т.е. становится ДУ I порядка линейным неоднородным, решаем его методом вариации произвольной постоянной. Сначала рассмотрим однородное уравнение:
, т.е. становится ДУ I порядка линейным неоднородным, решаем его методом вариации произвольной постоянной. Сначала рассмотрим однородное уравнение:
 всегда с разделяющимися переменными:
всегда с разделяющимися переменными:

 ищем общее решение неоднородного ДУ в таком же виде, только
ищем общее решение неоднородного ДУ в таком же виде, только  , т .е.
, т .е.
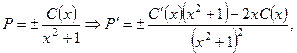 подставляя в неоднородное ДУ, получаем
подставляя в неоднородное ДУ, получаем
 Найдем
Найдем 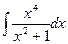 , выделив сначала целую часть дроби
, выделив сначала целую часть дроби  =
=
 получим
получим 
 . Тогда
. Тогда

Ответ: 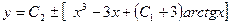 - общее решение исходного ДУ второго порядка.
- общее решение исходного ДУ второго порядка.
Задача №9. Найти решение задачи Коши 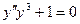 ,
,  ,
, 
Решение: Данное ДУ II порядка не содержит x, значит, сделаем замену переменных так:  ,
,  . Подставляя в исходное ДУ, т.е. получим
. Подставляя в исходное ДУ, т.е. получим  , т.е. ДУ I порядка сразделяющимися переменными
, т.е. ДУ I порядка сразделяющимися переменными

и сразу найдем С1, используя начальное условие  ,
,  .
.
Получим:  . Итак
. Итак 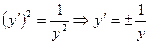 ДУ I порядка c разделяющимися переменными:
ДУ I порядка c разделяющимися переменными: 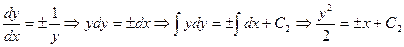 .
.
Найдем С2 , используя 
Ответ:  и
и  являются решениями задачи Коши.
являются решениями задачи Коши.
Задача №10.Найти общее решение дифференциального уравнения

Решение: Данное ДУ III порядка является линейным неоднородным с постоянными коэффициентами. Его общее решение имеет вид:  . Сначала найдем
. Сначала найдем  – общее решение однородного уравнения, соответствующего данному:
– общее решение однородного уравнения, соответствующего данному:  , его характеристическое уравнение имеет вид :
, его характеристическое уравнение имеет вид :  или
или  . Найдем корни этого уравнения:
. Найдем корни этого уравнения:  ,
, 
Следовательно, частные решения однородного уравнения, имеют вид 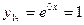 ,
,  ,
,  , а общее решение однородного уравнения
, а общее решение однородного уравнения 
 .
. 
 Т.к. правая часть неоднородного ДУ является многочленом второй степени, то и
Т.к. правая часть неоднородного ДУ является многочленом второй степени, то и  будем искать как многочлен второй степени с неопределенными коэффициентами
будем искать как многочлен второй степени с неопределенными коэффициентами 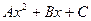 , но надо еще учесть, что
, но надо еще учесть, что  – простой корень характеристического уравнения, поэтому выражение
– простой корень характеристического уравнения, поэтому выражение 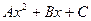 нужно умножить на x. Итак,
нужно умножить на x. Итак,  или
или 


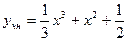

Ответ: 
Задача №11.Найти общее решение дифференциального уравнения

Решение: Решаем данное дифференциальное уравнение III порядка линейное неоднородное с постоянными коэффициентами также, как и предыдущее.
Сначала  имеет характеристическое уравнение
имеет характеристическое уравнение  ,
,  ,
, 
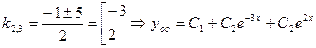 ,
,  , умножение на x вызвано тем, что
, умножение на x вызвано тем, что 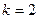 является простым корнем характеристического уравнения, и число 2 стоит множетелем при x в степени показательной функции
является простым корнем характеристического уравнения, и число 2 стоит множетелем при x в степени показательной функции  . Значит
. Значит 




 ;
; 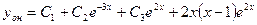
Ответ: 
Задача №12.Найти общее решение дифференциального уравнения

Решение: Данное ДУ II порядка линейное неоднородное с постоянными коэффициентами решаем также как и две предыдущие задачи:
Уравнение  имеет характеристическое уравнение
имеет характеристическое уравнение  - корень кратности два.
- корень кратности два. 




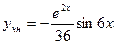

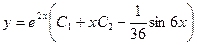
Задача №13.Найти общее решение дифференциального уравнения

Решение: Как и предыдущие три ДУ решаем это уравнение
 – характеристическое уравнение.
– характеристическое уравнение.  ,
,  ,
, 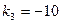 – его корни
– его корни 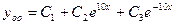
 . А – многочлен нулевой степени, соответствующий многочлену, стоящему в левой части уравнения, умножен на x, т.к.
. А – многочлен нулевой степени, соответствующий многочлену, стоящему в левой части уравнения, умножен на x, т.к.  – простой корень характеристического уравнения.
– простой корень характеристического уравнения.






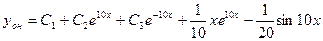
Ответ: 
Задача №14. Найти решение задачи Коши 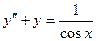 ,
, 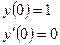
Решение: Данное ДУ решим методом вариации произвольных постоянных. Сначала решаем ДУ однородное:  , его характеристическое уравнение
, его характеристическое уравнение  , у нас
, у нас  ,
,  , значит,
, значит,  ,
, 
 ; Общее решение неоднородного уравнения ищется в том же виде, только
; Общее решение неоднородного уравнения ищется в том же виде, только  и
и  – искомые функции т.е
– искомые функции т.е  Для нахождение
Для нахождение  и
и  составим систему:
составим систему: 
из  и подставим в (2) системы, получим:
и подставим в (2) системы, получим: 
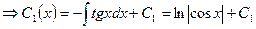 . Значит
. Значит 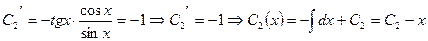
Итак,  или
или  Найдем С1 и С2 из начальных условий
Найдем С1 и С2 из начальных условий 
 . Следовательно, решением задачи Коши будет частное решение вида
. Следовательно, решением задачи Коши будет частное решение вида 
Ответ: 
7 РЯДЫ
Теоретический материал к разделу
7.1.1 Числовые ряды
Определение 1.Для заданной бесконечной последовательности чисел 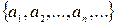 выражение
выражение
 , (1)
, (1)
где числа  - члены ряда, называется числовым рядом.
- члены ряда, называется числовым рядом.
Обозначим  и назовем частичными суммами ряда.
и назовем частичными суммами ряда.
Определение 2. Если существует предел частичной суммы ряда  то
то  называется суммой ряда (1).
называется суммой ряда (1).
Определение 3. Ряд называется сходящимся, если  - конечное число, иначе, т.е. если
- конечное число, иначе, т.е. если 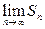 равен бесконечности или не существует, ряд называется расходящимся.
равен бесконечности или не существует, ряд называется расходящимся.
Очевидно, что отбрасывание конечного числа членов ряда не влияет на ее сходимость. Для сходящихся рядов


|
из
5.00
|
Обсуждение в статье: Теоретический материал к разделу |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

