 |
Главная |
Тема 6. Некоторые законы распределения случайной величины
|
из
5.00
|
Основные понятия по теме:
1. Биномиальное распределение.
2. Распределение Пуассона.
3. Равномерное распределение.
4. Показательное распределение.
5. Параметры распределений (математическое ожидание, дисперсия, среднее квадратическое отклонение).
6. Функция и плотность распределения вероятностей.
Применение этих понятий на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Случайная величина 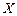 называется распределенной по биномиальному закону, если …
называется распределенной по биномиальному закону, если …
1*. 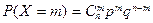
2. 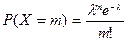
3. 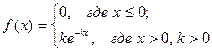
4. 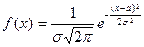
5. 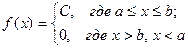 .
.
2. Случайная величина 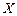 называется распределенной по закону Пуассона, если …
называется распределенной по закону Пуассона, если …
1. 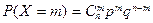
2.* 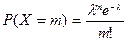
3. 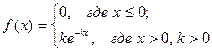
4. 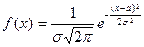
5. 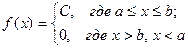 .
.
3. Случайная величина 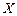 называется равномерно распределенной на интервале
называется равномерно распределенной на интервале 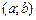 , если …
, если …
1. 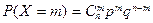
2. 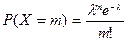
3. 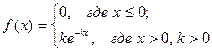
4. 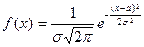
5. * 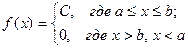 .
.
4. Математическое ожидание, дисперсия непрерывной случайной величины 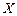 , распределенной по показательному закону
, распределенной по показательному закону 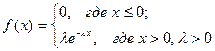 равны …
равны …
1. l, l
2. 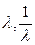
3*. 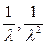
4. 1,0
5. 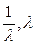
5. Случайная величина 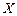 имеет показательное распределение, если …
имеет показательное распределение, если …
1. 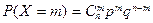
2. 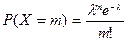
3.* 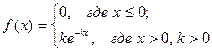
4. 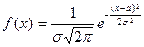
5. 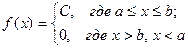 .
.
6. Случайная величина 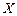 имеет нормальное распределение, если …
имеет нормальное распределение, если …
1. 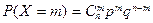
2. 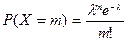
3. 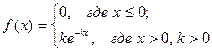
4.* 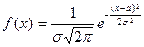
5. 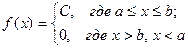 .
.
7. Случайная величина подчинена закону равномерного распределения на интервале 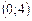 . Тогда ее математическое ожидание равно
. Тогда ее математическое ожидание равно
1*. 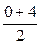
2. 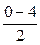
3. 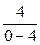
4. 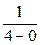
8. Случайная величина подчинена закону равномерного распределения на интервале 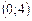 . Тогда ее плотность распределения равна …
. Тогда ее плотность распределения равна …
1) 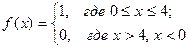
2) 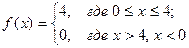
3) 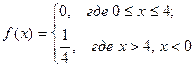
4)* 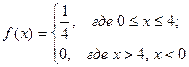
9. Математическое ожидание, дисперсия непрерывной случайной величины 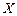 , биномиально распределенной случайной величины равны …
, биномиально распределенной случайной величины равны …
1) 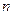 ;
; 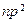 ;
;
2)* 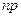 ,
, 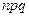 ;
;
3) 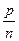 ;
; 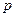 ;
;
4) 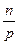 ;
; 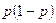 ;
;
5) 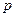 ,
, 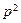 .
.
Тема 7. Нормальное распределение
Основные понятия по теме:
1. Нормальный закон. Его параметры.
2. Функция распределения вероятностей.
3. Плотность распределения вероятностей.
4. Кривая Гаусса (нормальная кривая).
5. Правило трех сигм.
6. Вероятность попадания в интервал.
Применение этих понятий на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Случайная величина 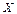 распределена по нормальному закону с
распределена по нормальному закону с 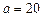 ,
, 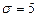 . Тогда
. Тогда 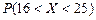 равна ...
равна ...
1)* 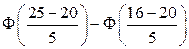 ;
;
2) 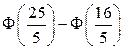 ;
;
3) 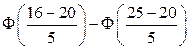 ;
;
4) 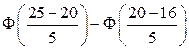
2. Случайная величина 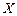 распределена по нормальному закону с
распределена по нормальному закону с 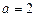 ,
, 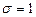 . Тогда
. Тогда 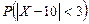 равна …
равна …
1) 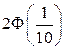 ;
;
2)* 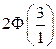 ;
;
3) 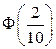 ;
;
4) 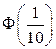 ;
;
5) 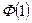
3. Дифференциальная функция нормально распределенной случайной величины 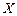 равна
равна 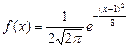 , тогда математическое ожидание и дисперсия случайной величины
, тогда математическое ожидание и дисперсия случайной величины 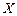 равны …
равны …
1) 2;2;
2)* 1;2;
3) 8;2
4) 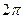 ;1
;1
5) 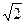 ;1
;1
4. На графике изображена кривая нормального распределения вероятностей:
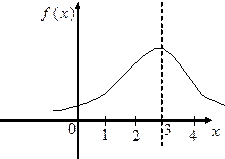
Математическое ожидание равно …
1) 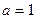 ;
;
2) 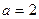 ;
;
3) * 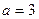 ;
;
4) 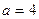 ;
;
5) 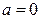
5. На рисунке изображены три нормальные кривые. Какой из нормальных кривых соответствует меньшее значение 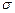 ?
?
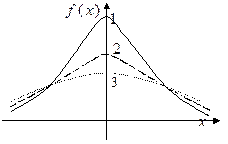
1) * 1;
2) 2;
3) 3;
4) вид нормальной кривой не зависит от 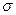 ;
;
5) другой ответ
6. На рисунке изображены три нормальные кривые. Меньшему значению 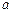 соответствует нормальная кривая …
соответствует нормальная кривая …
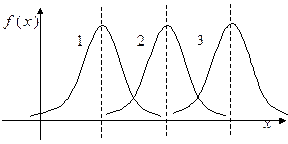
1) * 1;
2) 2;
3) 3;
4) положение нормальной кривой не зависит от параметра 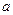 ;
;
5) другой ответ
|
из
5.00
|
Обсуждение в статье: Тема 6. Некоторые законы распределения случайной величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

