 |
Главная |
Бинарные отношения и их свойства
|
из
5.00
|
Основы дискретной математики.
Понятие множества. Отношение между множествами.
Множество – совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
Объекты, составляющие множество называются элементами множества. Для того чтобы некоторую совокупность объектов можно было называть множеством должны выполняться следующие условия:
· Должно существовать правило, по которому моно определить принадлежит ли элемент к данной совокупности.
· Должно существовать правило, по которому элементы можно отличить друг от друга.

Множества обозначаются заглавными буквами, а его элементы маленькими. Способы задания множеств:
· Перечисление элементов множества.  - для конечных множеств.
- для конечных множеств.
· Указание характеристического свойства  .
.
Пустым множеством – называется множество, не содержащее ни одного элемента (Ø).
Два множества называются равными, если они состоят из одних и тех же элементов.  ,
, 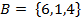
 A=B
A=B
Множество B называется подмножеством множества А (  , тогда и только тогда когда все элементы множества B принадлежат множеству A.
, тогда и только тогда когда все элементы множества B принадлежат множеству A.
Например:  , B
, B  =>
=> 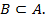
Свойство: 
Примечание: обычно рассматривают подмножество одного и того е множества, которое называется универсальным (u). Универсальное множество содержит все элементы.
Операции над множествами.
| A |
| B |
 Н-р:
Н-р:  ,
,  ,
,

2.Пересечением 2-х множеств называется новое множество, состоящее из элементов, одновременно принадлежат и первому и второму множеству.
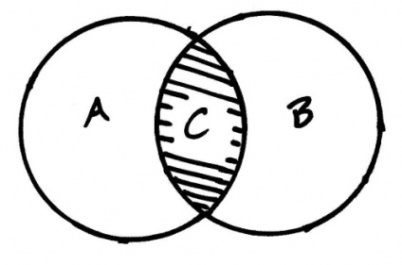
 Н-р:
Н-р:  ,
,  ,
,
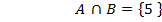
Свойство: операции объединения и пересечения.
· Коммутативность. 
 ;
;
· Ассоциативность.  ;
;
 ;
;
· Дистрибутивный. 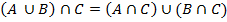 ;
;
 ;
;
| A |
| B |
 Н-р:
Н-р:  ,
,  ,
,

| А |

|
| U |
 ) называется множество состоящее из тех элементов множества U, которые не принадлежат множеству А.
) называется множество состоящее из тех элементов множества U, которые не принадлежат множеству А.


Бинарные отношения и их свойства.
Пусть А и В это множества производной природы, рассмотрим упорядоченную пару элементов (а, в) а ϵ А, в ϵ В можно рассматривать упорядоченные «энки».
(а1, а2, а3,…аn), где а1 ϵ А1; а2 ϵ А2; …; аn ϵ Аn ;
Декартовым (прямым) произведением множеств А1, А2, …, Аn , называется мн-во, которое состоит из упорядоченных nk вида  .
.
Н-р: М = {1,2,3}
М× М= М2 = {(1,1);(1,2);(1,3); (2,1);(2,2);(2,3); (3,1);(3,2);(3,3)}.
Подмножества декартова произведения  называется отношением степени n или энарным отношением. Если n=2, то рассматривают бинарные отношения. При чем говорят, что а1, а2 находятся в бинарном отношении R, когда а1 R а2.
называется отношением степени n или энарным отношением. Если n=2, то рассматривают бинарные отношения. При чем говорят, что а1, а2 находятся в бинарном отношении R, когда а1 R а2.
Бинарным отношением на множестве M называется подмножество прямого произведения множества n самого на себя.
М× М= М2 = {(a, b)| a, b ϵ M} в предыдущем примере отношение меньше на множестве М порождает следующее множество: {(1,2);(1,3); (2,3)}
Бинарные отношения обладают различными свойствами в том числе:
· Рефлексивность:  .
.
· Антирефлексивность (иррефлексивность):  .
.
· Симметричность:  .
.
· Антисимметричность: 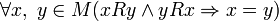 .
.
· Транзитивность:  .
.
· Асимметричность:  .
.
Виды отношений.
· Отношение эквивалентности;
· Отношение порядка.
v Рефлексивное транзитивное отношение называется отношением квазипорядка.
v Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
v Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.
v Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.
|
из
5.00
|
Обсуждение в статье: Бинарные отношения и их свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

