 |
Главная |
Операции с пустым и универсальным множествами
|
из
5.00
|
Обозначение
1) Указанием определяющего свойства A = { x | P(x) }
2) Перечислением элементов A = { x1, x2, …, xn }
Основные понятия:
1) пустое множество, обычно обозначается символом Ø (в нем совсем ничего нет);
2) подмножество (множество, элементы которого являются элементами множества, которому принадлежит подмножество) и надмножество (множество элементов множества, которые не вошли в подмноество);
3) пространство (универсальное множество – множество вообще всевозможных элемнтов);
Мощность множества – количество элементов в множестве.
| A | = n
Принцип включения и исключения
Принципом включения и исключенияназывается формула, позволяющая вычислить мощность объединения множеств, если известны их мощности и мощности всех пересечений.
Рассмотрим частные случаи этой формулы для двух и трех множеств:


Справедливы аналогичные формулы и для пересечения множеств:


2. Операции над множествами.
· пересечение – когда «х» и в одном и в другом множестве

· объединение – когда «х» либо в одном либо в другом множествах

Если множества A и B не пересекаются:  , то их объединение обозначают также:
, то их объединение обозначают также:  .
.
· разность (дополнение) – когда «х» только в А но не в В
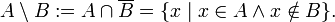
· Декартово или прямое произведение – перемножение всевозможных пар элементов
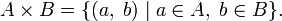
Покрытие множества – семейство множеств, такое, что их объедение дает исходное множество.
Разбиение множества – представление множества в виде непересекающихся элементов.
Количество разбиений – полиномиальный коэффициент:

ПОЛЕ – множество с двумя внутренними ассоциативными и коммутативными бинарными операциями, связанными законом дистрибутивности. По первой операции есть нейтральный и обратный элементы для каждого. По второй операции – есть нейтральный для каждого кроме нейтрального по первой операции. (пример: Поле действительных чисел с операциями сложения и умножения)
Поле из конечного числа элементы – поле Галуа(французский математик ^_^)
GF(2) – поле из 2 элементов.
3. Универсальное множество.
Универсальное множество — в математике множество, содержащее все мыслимые объекты. Универсальное множество единственно. Обозначается буковкой I.
· Любой объект, какова бы ни была его природа, является элементом универсального множества:

· Любое множество является подмножеством универсального множества:

· Объединение универсального множества с любым множеством равно универсальному множеству.

· В частности, объединение универсального множества с самим собой равно универсальному множеству.

· Пересечение универсального множества с любым множеством равно последнему множеству.

· В частности, пересечение универсального множества с самим собой равно универсальному множеству.

· Исключение универсального множества из любого множества равно пустому множеству.

· В частности, исключение универсального множества из себя равно пустому множеству.
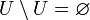
· Исключение любого множества из универсального множества равно дополнению (всему тому, что не является этим множеством :DD) этого множества.

· Дополнение универсального множества есть пустое множество.

4. Основные тождества алгебры множеств.
Для любых множеств A, B, C справедливы следующие тождества:
Коммутативность.
а) A È B = B È A (для объединения);
б) A Ç B = B Ç A (для пересечения).
Ассоциативность.
а) A È (B È C) = (A È C) È C (для объединения);
б) A Ç (B Ç C) = (A Ç B) Ç C (для пересечения).
Дистрибутивность.
а) AÈ (BÇC) = (AÈB) Ç (AÈC) (для объединения относительно пересечения);
б) AÇ(BÈC) = (AÇB)È(AÇC) (для пересечения относительно объединения).
Закон де Моргана.
а)  =
=  Ç
Ç  (дополнение к объединению есть пересечение дополнений);
(дополнение к объединению есть пересечение дополнений);
б)  =
=  È
È  (дополнение к пересечению есть объединение дополнений).
(дополнение к пересечению есть объединение дополнений).
Поглощение.
а) A È (A Ç B) = A;
б) A Ç (A È B) = A.
Двойное дополнение.
 = A.
= A.
7. Закон исключенного третьего. 
A È  = U.
= U. 
Операции с пустым и универсальным множествами.
| а) A È U = U; б) A È Æ = A; | в) A Ç U = A;  г) A Ç Æ = Æ;
г) A Ç Æ = Æ;
| д)  = U;
е) = U;
е) 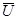 = Æ. = Æ.
|
Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если xÎ А, то xÎВ и, во-вторых, если xÎВ, то xÎ А.
5. Декартово произведение множеств.
Декартовым (прямым) произведениеммножеств А и В (обозначение AxB) называется множество всех упорядоченных пар (a, b), таких, что a ∈ A и b ∈ B.
В частности, если А = В, то обе координаты принадлежат множеству А, такое произведение обозначается А2. Аналогично, прямым произведением множеств A1, A2, ... An называется множество всех векторов (a1, a2, ... an) длины n, таких, что a1 ∈ A1, a2 ∈ A2 ... an ∈ An.
6. Бинарные отношения на множестве.
Бинарным отношением из множества A в множество B называется некоторое подмножество декартового произведения AxB
Отношения в дальнейшем будем обозначать ρ

(читается ρ отношение из A в B)
Отношения:
· Обратное отношение (отношение, обратное к R) — это бинарное отношение, состоящее из пар элементов (у, х), полученных перестановкой пар элементов (х, у) данного отношения R. Обозначается: R−1. Для данного отношения и обратного ему верно равенство: (R−1)−1 = R.
· Рефлексивное отношение — двухместное отношение R, определённое на некотором множестве и отличающееся тем, что для любого х этого множества элемент х находится в отношении R к самому себе, то есть для любого элемента х этого множества имеет место x R x. Примеры рефлексивных отношений: равенство
· Транзитивное отношение — двухместное отношение R, определенное на некотором множестве и отличающееся тем, что для любых х, у, z этого множества из x R y и y R z следует xRz (xRy&yRz 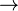 xRz). Примеры транзитивных отношений: «больше», «меньше»
xRz). Примеры транзитивных отношений: «больше», «меньше»
7. Основные свойства бинарных отношений: рефлексия, симметричность, транзитивность.
Отношение эквивалентности — бинарное отношение R между предметами х и у, удовлетворяющее следующим свойствам:
1.свойству рефлексии: x R x (предмет находится в отношении R к самому себе);
2.свойству симметричности: x R y -> y R x (если предмет х находится в отношении R к предмету у, то и у находится в отношении R к х);
3.свойству транзитивности: x R y & y R z -> x R z (если предмет х находится в отношении R к предмету у и у находится в отношении R к z, то х находится в отношении R к z).
Таким образом, отношение типа равенства является одновременно рефлексивным, симметричным и транзитивным. Пример отношения, которое удовлетворяет свойству (3), но не удовлетворяет свойствам (1) и (2): «больше».
8. Отношение эквивалентности.
Отношение эквивалентности (~) на множестве X — это бинарное отношение, для которого выполнены следующие условия:
1. Рефлексия: a ~ a для любого a в X,
2. Симметричность: если a ~ b, то b ~ a,
3. Транзитивность: если a ~ b и b ~ c, то a ~ c.
Запись вида «a ~ b» читается как «a эквивалентно b».
9. Отображения множеств.
Если каждому элементу x множества X поставлен в соответствие ровно один элемент ƒ(x) множества Y, то говорят, что задано отображение ƒ из множества X в множество Y.
При этом, если ƒ(x)=y, то элемент y называется образом элемента x при отображении ƒ, а элемент x называется прообразом элемента y при отображении ƒ.
Обозначение: ƒ: X→Y.
Функция – взаимно-однозначное отображение одного множества на другое.
10. Основные понятия и определения теории графов.
Граф -система, которая интуитивно может быть рассмотрена как множество кружков и множество соединяющих их линий.
Кружки называются вершинамиграфа, линии со стрелками - дугами,без стрелок -ребрами.
Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным;
Граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным.
Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными
Для любого графа есть матрица смежности.
Петля – дуга, которая соединяет вершину саму с собой. Петля при подсчете степени вершины берется дважды!!!!!
Планарный граф – все точки лежат в одной плоскости.
Раскрашенные графы – вершины при соединении красятся в разные цвета.
ПОЛНЫЙ ГРАФ – такой граф, все вершины которого соединены друг с другом ребрами.
Начало теории графов датируют 1736 г, когда Л. Эйлер решил популярную в то время «задачу о кенигсбергских мостах». Термин «граф» впервые был введен спустя 200 лет (в 1936) Д. Кенигом.
11. Ориентированные и неориентированные графы.
Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным;
Граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным.
Из ориентированного графа сделать неориентированный граф – убрать стрелки
12. Способы задания графов: аналитический, геометрический, матричный. Матрицы смежности и инцидентности графа. Маршруты, циклы и цепи графа.
1. Геометрический способ задания графа– ну, просто нарисовать его таким, какой он есть.
2. Матрицей смежности – берем две вершины. Если между ними есть дуга или ребро – то пишем 1, нет – 0.
3. Матрица инцидентности – берем вершину. Если из нее выходит дуга - пишем 1, входит - -1, нет – 0.
Матрицу инцидентности можно построить для ориентированных и неориентированных графов.
Вершина, соединенная с ребром – инцидентна.
Две вершины соединенные ребром – смежные.
Инцидентность — понятие, используемое только в отношении ребра и вершины: если v1, v2 - вершины, а e = (v1, v2) — соединяющее их ребро, тогда вершина v1 и ребро e инцидентны, вершина v2 и ребро e тоже инцидентны. Две вершины (или два ребра) инцидентными быть не могут. Для обозначения ближайших вершин (рёбер) используется понятие смежности.
Маршрут в графе — это чередующаяся последовательность вершин и рёбер v0, e1, v1, e2, v2, …, ek, vk, в которой любые два соседних элемента инцидентны. Если v0 = vk, то маршрут замкнут, иначе открыт.
Маршрут, в котором ребра не повторяются – цепь (путь). Длина пути для ориентированного графа – количество дуг (ребер).
Цепи, у которых начала и концы совпадают – циклы.
13. Связность графов.
Связный граф – из любой вершины есть маршрут в другую (матрица связности для такого графа состоит из единиц только)
матрица связности – в ней 0 и 1
1 – из одной вершины есть маршрут в другую
0 – нет маршрута.
14. Эйлеровы графы.
Граф Эйлера – в котором существует цикл.
Эйлеров граф – в нем есть маршрут, проходящий через все дуги по одному разу.
Цикл - это путь длины не менее 1, который начинается и заканчивается в одной и той же вершине.
15. Высказывания простые и составные.
Простое высказывание – оно простое. «Я – задрот» - простое высказывание.
Составное – содержит в себе несколько высказываний, соединенных логическими операциями (^, v, не, ->)
«Я задрот и форевер элон» - составное высказывание. ;D
16. Логические операции. Таблицы истинности.
Логическая операции – конъюнкция, дизъюнкция, отрицание, следование.
Один из способов задания логической операции – таблицей истинности.
Для каждой парочки 0 и 1 ставится в соответствие 0 или 1, т.о. задается логическая операция.
17. Булевы функции и формулы алгебры высказываний. ДНФ и КНФ.
Булевы функции – любые функции от 0 и 1. всего их 2^
Логическая функция – когда любым двум элементам ставится в соответствие элемент из этого же множества.
Логическая функция – только ^ v -> не. В добавок к ним пара булевых (не являющимися логическими) функций:
Штрих Шеффера (анти конъюнкция). Интересно отметить, что: 
| x | y | x|y |
Стрелка Пирса (Лукашевича). В действительности: 
| x | y | x ↓y |
Дизъюнктиивная нормальная форма (ДНФ)— форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ (я бы не рискнул так громко об этом заявлять ахахах). Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Конъюнктивная нормальная форма (КНФ) форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов.
Алгоритм построения КНФ и ДНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

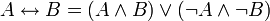
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
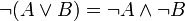

3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Также можно использовать следующие свойства:
1) Ассоциативность
(X v Y) v Z = X v (Y v Z)
2) Коммутативность
X v Y = Y v Z
3) Дистрибутивность
X ^ Y v X ^ Z = X ^ (Y v Z)
XY v X notY = X ^ (Y v notY) = X – минимальная дизъюнктивная нормальная форма.
Y v notY = 1
18. Преобразования формул в СДНФ и СКНФ.
из КНФ в СКНФ:
Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение: 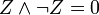 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:
(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:

Таким образом, из КНФ получена СКНФ.
из ДНФ в СДНФ:
Если в какой-то простой конъюнкции недостает переменной, например, Z, вставляем в нее выражение:  , после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
, после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
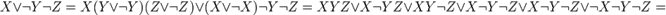

Таким образом, из ДНФ получили СДНФ.
А вообще, еще можно построить по таблице истинности. Для этого берем таблицу истинности.
Смотрим на значения функции. Если хотим строить СНДФ, то смотрим на те, где 1. Строим на значения переменных, при которых получено это значение. Строим конъюнктивная выражение с этими переменными так, чтобы вышла единица. Так делаем со всеми значениями-единицами в табличке. Полученные выражения разделяем дизъюнкцией.
Если хотим строить СКНФ, то смотрим на те, где 0. Строим дизъюнктивные выражения с переменными, при которых получены эти нули и соединяем их конъюнкцией.
19. Многочлены Жегалкина.
Многочлен Жегалкина – многочлен над полем GF(2), в котором в качестве умножения используется конъюнкция, а в качестве сложения – сложение по модулю 2.
Многочлен Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально многочлен Жегалкина можно представить в виде


Любую булеву функцию можно выразить через многочлен Жегалкина.
На самом деле, вот это вот куда проще, чем он объяснял.
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
| · Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000…00 до 111…11. · Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. · Ячейка в каждом последующем столбце получается путём суммирования по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. · Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. · Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т. д. · Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина. | 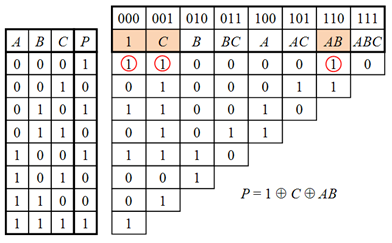
|
20. Основные понятия и определения комбинаторики.
 - число перестановок (упорядочивание)
- число перестановок (упорядочивание)
 - число перемещений (число размещений)
- число перемещений (число размещений)
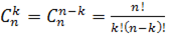 - число сочетаний (без учета порядка)
- число сочетаний (без учета порядка)
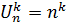 - число сочетаний с возвращениями с учетом порядка
- число сочетаний с возвращениями с учетом порядка
 - число сочетаний с возвращениями без учета порядка (число сочетаний с повторениями)
- число сочетаний с возвращениями без учета порядка (число сочетаний с повторениями)
21. Бином Ньютона. Свойства биномиальных коэффициентов. Перестановки с повторениями.
 – бином Ньютона
– бином Ньютона
 - биномиальные коэффициенты.
- биномиальные коэффициенты.
Свойства биномиальных коэффициентов:
1.Сумма коэффициентов разложения (a + b)n равна 2n
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:

3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то k1 + k2 + …+ km = n и количество всевозможных перестановок с повторениями равно полиномиальному коэффициенту: 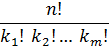
22. Связь комбинаторики с элементами теории конечных множеств.
Множество и элемент множества относятся к числу первичных понятий, для которых не существует определений в строгом смысле слова. Поэтому обычно говорят о множестве как о наборе предметов (элементов множества), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.
На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т. д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют "комбинаторные задачи".
Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества.
23. Основные понятия и определения теории кодирования.
зд. Информация – жизненно важные изменения окружающей среды, на которые мы реагируем.
Информация измеряется в битах.
Речь – способ передачи информации у людей.
зд. Речь – универсальная система кодирования информации. Передать знания ~ рассказать речью.
Универсальный способ представления информации – письменность.
Алфавитные коды:
A = { a1, …. ,an }
B = { b1, …, bm }
Любая последовательность символов в теории кодирования – слово: ai1, ai2, aik
Код – (1) правило, описывающее соответствие знаков или их сочетаний одного алфавита знакам или их сочетаниям другого алфавита; - (2) знаки вторичного алфавита, используемые для представления знаков или их сочетаний первичного алфавита.
КОДИРОВАНИЕ – иное представление информации (~ к слову одного алфавита ставить взаимно-однозначно слово из другого алфавита). Каждый символ исходного алфавита заменяется не обязательно на один символ, но и может на целое слово.
24. Кодирование и декодирование.
Кодирование – перевод информации, представленной посредством первичного алфавита, в последовательность кодов.
Декодирование - операция, обратная кодированию, т.е. восстановление информации в первичном алфавите по полученной последовательности кодов.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо ее потерь.
+ Красиво рассказать про шифр Цезаря и достаточно.
25. Алфавитное кодирование.
Пусть есть два каких-то алфавита:
A = { a1, …. ,an }
B = { b1, …, bm }
суть алфавитного кодирования в том, что каждому символу алфавита А ставится в соответствие символ алфавита В.
Префикс – первая часть слова
Суффикс – вторая часть слова.
26. Проблема взаимной однозначности алфавитного кодирования.
Есть два алфавита -
A = { а, б, в, … я}
B = { . - }
| б -… | е . | н -. | о --- |
Слово «небо» = «-..--…---» Неоднозначное кодирование. Потому что при декодировании будут проблемы с различимостью символов. Чтобы такой проблемы избежать надо во второй алфавит добавить еще один символ, который будет суффиксом каждого кода. Например, пробел – «_» (дописать его к каждому коду в таблице)
тогда: «небо» = «-. . -… ---» Однозначное кодирование. Можно расшифровать.
Однозначное кодирование – тогда, когда код не является префиксом другого.
27. Свойство префикса алфавитного кодирования.
Свойство префиксности – когда код не является суффиксом другого (когда в конце есть пробел) + все, что в предыдущем билете.
28. Признаки взаимной однозначности алфавитного кодирования.
Если часть кода однозначно декодируется (ну, на примере Морзе – каждую хрень из точки и тире можно представить ОДНОЙ И ТОЛЬКО ОДНОЙ буквой) то такое кодирование взаимно-однозначное. + опять же, предыдущие билеты
29. Самокорректирующиеся коды и их свойства.
Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися.
Главное задача – при передаче информации в двоичном виде возможны искажения этой информации.
Искажение – связаны не с потерей, а с изменением двоичных символов. (замена одного символа на другой)
+ следующие билеты!
30. Коды Хемминга. Соотношение между числом информационных и контрольных символов кода Хемминга.
Nk куичные коды
1. Берем последовательность k длиной q (их всего qk)
2. Берем последовательность из n элементов, так, что n > k
3. Каждому коду последовательности k ставим в соответствие код из последовательности n.
nk-двоичный код – когда q = 2.
Код Хэмминга – код, исправляющий единичную ошибку. Работает на двоичной системе счисления. Является алфавитным, блоковым nk-двоичным кодом.
Введем обозначения:
k – количество информационных бит
n – длина кодового слова
m – количество проверочных бит
Для кода Хемминга справедливо следующее соотношение:
k + m + 1 = 2m Также, не стоит забывать, что m + k = n
| k/n | n | k | m |
| 0.3 | |||
| 0.57 | |||
| 0.63 | |||
| 0.84 | |||
| 0.98 |
k/n – отношение k к n – доля информационных символов в кодовом слове.
Из этого видно, что чем больше m – тем эффективнее код Хэмминга, т.к. доля информационных бит возрастает.
31. Процесс кодирования Хемминга.
Код Хэмминга строится путем умножения исходного слова на порождающую матрицу (она составит из базисных векторов – информационных битов и проверочных битов, которые проверяют, не было ли ошибки)
Например, построим 7,4 блоковой двоичный код (4 информационных, 3 проверочных)
| 20 | 21 | 21 + 20 | 22 | 22 + 20 | 22 + 21 | 22 + 21 + 20 |
| П1 | П2 | И3 | П4 | И5 | И6 | И7 |
| И3 = П1 + П2 И5 = П4 + П1 И6 = П4 + П2 И7 = П1 + П2 + П4 | П1 = И3 + И5 + И7 П2 = И3 + И6 + И7 П4 = И5 + И6 + И7 Чтобы код обнаруживал две ошибки, а исправлял одну можно добавить восьмой бит: π8 = П1 + П2 + И3 + П4 + И5 + И6 + И7 |
Систематические коды – содержат информационные биты и проверочные.
32. Процесс декодирования Хемминга, исправляющего не более чем одну ошибку
Не пониманию, почему тут декодирование, но я хотел бы рассказать про кодирование. И о том, как построить порождающую матрицу.
Для удобства, используем порядок символов из Хэмминга (П1 П2 И3 П4 И5 И6 И7). У нас есть сообщение: (1 1 0 1). Его надо помножить на матрицу, чтобы получить код Хэмминга.
|
|
Рассчитаем первый столбец матрицы: П1 по формуле П1 = И3 + И5 + И7
Второй столбец П2 = И3 + И6 + И7 . Т.е. если бит есть в формуле то ставим 1, если его нет – 0. Тупо, но работает ^_^
33. Кодовое расстояние
Кодовое расстояние – минимальное расстояние всех векторов из К.
pk k C pn
min ρ(a,b) = d(k); a,b ∈ K
I. Блочный код К обнаруживает любые t и меньше ошибок, тогда и только тогда, когда d(k) >= t + 1
II. Блочный код К может исправить любые t ошибок в коде когда d(k) >= 2t + 1
34. Линейные пространства над конечными полями
Конечное поле, состоящее из n элементов, мы будем обозначать Fn.
По поводу конечных полей мы будем предполагать известными следующие факты:
1) для любого n = pm, где p — простое число, существует единственное (с точностью до изоморфизма) поле из n элементов;
2) поле из n элементов существует только в том случае, когда n = pm, где p — простое число.
Для поля из n = pm элементов, где p — простое число, это число p называют характеристикой.
Линейные пространства над конечными полями определяются точно так же, как линейные пространства над R или над C, но у них, конечно, есть некоторые специфические свойства.
Прежде всего, отметим, что линейное пространство размерности k над полем Fn состоит из nk векторов. Действительно, любой вектор этого пространства имеет вид (x1, . . . , xk), где каждая из координат xi принимает любое из n возможных значений.
Если поле Fn содержит Fmв качестве подполя, то Fnявляется линейным пространством над Fmнекоторой размерности k, поэтому n = mk.
В частности, поле F8 не содержит подполя F4. И вообще, если поле Fpn содержит подполе Fpm , то n = mk для некоторого натурального числа k.
35. Метрика Хемминга
Начать стоит с определения Эвклидова пространства.
Эвклидово пространство – пространство арифметическое над полем действительных чисел. Бесконечное, мать его.
Там есть скалярное произведение. Свойства его таковы:
1. (a, b) = (b, a)
2. (a + g, b) = (a, b) + (g, b)
3. (aR,b) = R(a,b)
4. (a,a) >= 0 (не выполняется в GF(2)); a=0 => (a,a)=0
Вообще, мы считаем скалярным произведением – длину одного вектора помноженную на длину другого и cos угла между ними. Но есть другой способ:
A = (a1, a2, …, an)
B = (b1, b2, …, bn)

Норма (длина) вектора: 
Расстояние между векторами ρ(a,b) = ||a-b||
Свойства:
1. ρ(a,b) > 0 a≠b (a=b => ρ=0)
2. ρ(a,b) = ρ(b,a)
3. ρ(a,b) <= ρ(a,g) + ρ(g,b) (неравенство треугольника)
Все они выполняются для GF(2) и называются Метрикой Хэмминга.
Метрика (длина) вектора – количество не совпавших его компонентов.
Метрика Хэмминга – число не совпавших элементов в векторах.
Свойства этой метрики:
1. ||a|| > 0, a ≠ 0
2. ||a,r|| = ||a||
3. ||a + b|| <= ||a||+||b||
|
из
5.00
|
Обсуждение в статье: Операции с пустым и универсальным множествами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

