 |
Главная |
Композиция отображений
|
из
5.00
|
Булевы функции одной переменной.
При n=1 существуют 4 булевы функции:
| x | 
| 
| 
| 
|


тождественный нуль тождественная единица
Высказывание – это утверждение, о котором можно сказать истинно оно или ложно.
Высказыванияобозначаются латинскими буквами строчными или прописными, также можно использовать индексы.
Отрицанием,или инверсией, высказывания  называется высказывание
называется высказывание  , которое истинно, когда высказывание
, которое истинно, когда высказывание  ложно, и ложно, когда
ложно, и ложно, когда  истинно.
истинно.
Дизъюнкцией (нестрогой или соединительной) высказываний  и
и  называется высказывание
называется высказывание  , которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.
, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.
Конъюнкцией высказываний  и
и  называется высказывание
называется высказывание  , которое истинно тогда и только тогда, когда истинны оба высказывания.
, которое истинно тогда и только тогда, когда истинны оба высказывания.
Строгой дизъюнкцией высказываний  и
и  называется высказывание
называется высказывание  (
(  ), которое истинно тогда и только тогда, когда истинно только одно из этих высказываний.
), которое истинно тогда и только тогда, когда истинно только одно из этих высказываний.
Импликацией высказываний  и
и  называется высказывание
называется высказывание  , которое ложно тогда и только тогда, когда из истины следует ложь.
, которое ложно тогда и только тогда, когда из истины следует ложь.
Эквиваленциейвысказываний  и
и  называется высказывание
называется высказывание  , которое истинно тогда и только тогда, когда либо истинны, либо ложны одновременно оба высказывания.
, которое истинно тогда и только тогда, когда либо истинны, либо ложны одновременно оба высказывания.
2.
Алгебра логики.
Булева алгебра.
Булевы функции двух переменных.
Таблица истинности
Булева алгебра служит основой для описания логики работы аппаратных и программных средств ЭВМ.
Алгебра логики использует логические переменные, которые принимают значения 0 и 1.
Рассмотрим множество  . Отображение
. Отображение  назовем булевой функцией n переменных.
назовем булевой функцией n переменных.
Булевы функции двух переменных.
При n=2 существуют 16 булевых функций:

| 
|  0 0
| 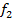 
| 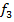
| 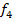 
| 
|  
|  
|  
| 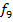 
|  
|  
| 
| 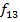 
|  
|  | |
|  1 1
|
Эти функции можно разделить на 3 группы:
1)симметрические функции:
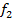 – конъюнкция,
– конъюнкция,  , логич. умножение, логич. И;
, логич. умножение, логич. И;
 – дизъюнкция,
– дизъюнкция,  , логич. сложение, логич. ИЛИ;
, логич. сложение, логич. ИЛИ;
 – эквиваленция,
– эквиваленция,  (одинаковые – 1; разные – 0);
(одинаковые – 1; разные – 0);
 – сумма по модулю 2,
– сумма по модулю 2,  , строгая дизъюнкция,
, строгая дизъюнкция, 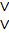 ;
;
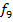 – стрелка Пирса,
– стрелка Пирса,  - является отрицанием дизъюнкции;
- является отрицанием дизъюнкции;
 – штрих Шеффера, | - является отрицанием конъюнкции.
– штрих Шеффера, | - является отрицанием конъюнкции.
Все эти функции симметричны по аргументам.
2)импликации (следования)
 – (из правды – ложь
– (из правды – ложь  ложь)
ложь)
3)функции, явно зависящие от одной переменной
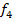 ,
,  ,
,  ,
, 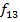
1, 16 нуль и единица
3, 5, 12 – ?
3.
Законы логики.
Равносильные преобразования
Равносильности формул логики называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств.
Законы логики
1.  закон тождества
закон тождества
2.  закон противоречия
закон противоречия
3.  закон исключенного третьего
закон исключенного третьего
4.  закон двойного отрицания
закон двойного отрицания
5. 

закон идемпотентности

6. 
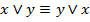
закон коммутативности (переместительный)
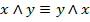
7. 

закон ассоциативности
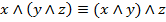
8. 

закон дистрибутивности

9. 

законы де Моргана
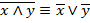
10. 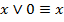

11. 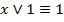

12. 

законы поглощения

13. 
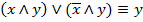
законы склеивания

Расшифровка первых пяти:
1. I закон сформулирован Аристотелем. Закон утверждает, что мысль, заключённая в некотором высказывании, остаётся неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует.
2. Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием.
3.Этот закон говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно, либо ложно, третьего не дано.
4. Закон двойного отрицания. Отрицать отрицание высказывания – то же, что и утверждать это высказывание.
5. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция (дизъюнкция) одинаковых сомножителей равносильна одному из них.
Доказать законы логики можно с помощью:
1) таблиц истинности;
2) равносильных преобразований.
Равносильные преобразования?
4.
Минимизация булевых функций.
Дизъюнктивная нормальная форма.
Совершенная дизъюнктивная нормальная форма
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Элементарной конъюнкцией (ЭК) называется выражение, состоящее из конечного числа переменных и их отрицаний, взятых в этом выражении не более одного раза и разделенных операциями конъюнкции. Например,  .
.
Дизъюнктивной нормальной формой(ДНФ)называется дизъюнкция конечного числа элементарных конъюнкций.
Дизъюнктивная нормальная форма называется совершенной, если в каждой ее элементарной конъюнкции представлены все переменные, входящие в данную функцию (либо сами, либо с отрицанием). Сокращенно СДНФ.
ВСЁ?
5.
Минимизация булевых функций.
Конъюнктивная нормальная форма.
Совершенная конъюнктивная нормальная форма
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Элементарной дизъюнкцией (ЭД) называется выражение, состоящее из конечного числа переменных и их отрицаний, взятых в этом выражении не более одного раза и разделенных операциями дизъюнкции. Например, 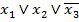 .
.
Конъюнктивной нормальной формой(КНФ)называется конъюнкция конечного числа элементарных дизъюнкций.
Конъюнктивная нормальная форма называется совершенной, если в каждой ее элементарной дизъюнкции представлены все переменные, входящие в данную функцию (либо сами, либо с отрицанием). Сокращенно СКНФ.
ВСЁ?
6.
Минимизация булевых функций.
Приведение ДНФ к СДНФ, к КНФ
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Чтобы привести ДНФ к СДНФ, нужно дополнить ЭК на множитель, содержащий недостаточную переменную и ее отрицание.


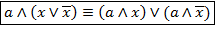
КАК К КНФ?
7.
Минимизация булевых функций.
Приведение КНФ к СКНФ, к ДНФ
Минимизация булевых функций – замена громоздких булевых функций им равносильными, но более простыми, используя законы алгебры логики.
Минимизировать булевы функции надо, приводя их к так называемой нормальной форме.
Существуют две разновидности нормальных форм – дизъюнктивная (ДНФ) и конъюнктивная (КНФ).
Чтобы привести КНФ к СКНФ нужно добавить в неполную ЭД слагаемое, содержащее конъюнкцию недостающей переменной и ее отрицания.



КАК К ДНФ?
8.
Логика предикатов
Предикатом называется сказуемое суждения, т.е. то, что утверждается или отрицается относительно объекта этого суждения.
«Он получил специальность программиста» - пример предиката.
Предикат становится высказыванием, если вместо местоимения подставить конкретный объект.
«М. А. Иванов стал программистом» (истина).
Язык логики предикатов
Символами X, Y, Z,  ,
,  … в логике предикатов принято обозначать предметные переменные, т.е. отдельные предметы – имена. Они могут быть простыми или сложными. Если такие предметы (имена) не содержат дополнительной информации о себе, то они называются собственными (простыми), например, «земля», «студент» и др.
… в логике предикатов принято обозначать предметные переменные, т.е. отдельные предметы – имена. Они могут быть простыми или сложными. Если такие предметы (имена) не содержат дополнительной информации о себе, то они называются собственными (простыми), например, «земля», «студент» и др.
Если такое имя содержит наряду с самим предметом его отдельные свойства, то оно является сложным, например «перпендикулярные прямые», «автор романа «Анна Каренина»» и др.
Рассмотрим предикат
x  y+2
y+2
где x определен на множестве 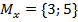
y – на множестве 
Сравним предикаты 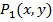 и
и 

| x  y+2 y+2
| 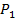
| 
|  x+2 x+2
| 
|
| (3;1) | 3  1+2 1+2
| (1;3) | 1  3+2 3+2
| ||
| (3;5) | 3  5+2 5+2
| (1;5) | 1  5+2 5+2
| ||
| (3;8) | 3  8+2 8+2
| (5;3) | 5  3+2 3+2
| ||
| (5;1) | 5  1+2 1+2
| (5;5) | 5  5+2 5+2
| ||
| (5;5) | 5  5+2 5+2
| (8;3) | 8  3+2 3+2
| ||
| (5;8) | 5  8+2 8+2
| (8;5) | 8  5+2 5+2
|
Одноместный предикат называется предикатом-свойством.
Двухместный и более предикат называется предикатом-отношением.
0-местный предикат называется высказыванием.
Полный прообраз единицы при предикате P называется множеством истинности предиката.


Если множество истинности предиката совпадает с его областью определения, то такой предикат называется тождественно истинным. И тождественно ложным, если множество истинности предиката пустое.
9.
Кванторы всеобщности и существования.
Построение операций к предикатам
Для количественных характеристик обычно используют понятия «все», «некоторые», «существуют» и др., которые называют кванторами(от лат. quantum – сколько). Мы часто пользовались символами 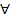 и
и  , заменяющими слова «любой» и «существует». Покажем действие этих кванторов в высказывательных формах. Часть формулы, на которую распространяется действие квантора, называется областью действия этого квантора. Вхождение переменной в формулу может быть связанным , если переменная расположена либо непосредственно после знака квантора, либо в области действий квантора, после которого стоит переменная. Все прочие вхождения – свободные. Например, в выражении
, заменяющими слова «любой» и «существует». Покажем действие этих кванторов в высказывательных формах. Часть формулы, на которую распространяется действие квантора, называется областью действия этого квантора. Вхождение переменной в формулу может быть связанным , если переменная расположена либо непосредственно после знака квантора, либо в области действий квантора, после которого стоит переменная. Все прочие вхождения – свободные. Например, в выражении  переменная x связывает свойства предиката и квантор общности.
переменная x связывает свойства предиката и квантор общности.
 - для любого x верно P(x)
- для любого x верно P(x)
 - существует x, для которого выполняется P(x).
- существует x, для которого выполняется P(x).
10.
Множества.
Задание множеств
Совокупность элементов, объединенных некоторым признаком, свойством, составляет понятие множество. Например, множество книг в библиотеке, множество студентов в группе, множество натуральных чисел N и т.д.
Запись  означает: элемент a принадлежит множеству M, т.е. элемент a обладает некоторым признаком. Аналогично
означает: элемент a принадлежит множеству M, т.е. элемент a обладает некоторым признаком. Аналогично  читвется так: элемент a не принадлежит множеству М.
читвется так: элемент a не принадлежит множеству М.
Множество считается заданным, если или перечислены все его элементы, или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству.
Первый вариант записывается так:  , например, M={0;1}.
, например, M={0;1}.
Последний вариант записывается так: M={b|P(b)}.Такая запись читается так: M состоит из тех (всех) элементов b, которые обладают признаком P. Например, M={n|n 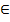 N,n<5} означает: М составляют только те натуральные числа, что меньше пяти.
N,n<5} означает: М составляют только те натуральные числа, что меньше пяти.
Само свойство Р будем называть характеристикой.
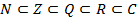
 |  | ||||||
 | |||||||
 |
нат. цел. рацион. действ. компл.
 - включение (для двух множеств)
- включение (для двух множеств)
Изображение множеств
Диаграммы Эйлера-Венна
 |  | ||||
 |
Множество K называется подмножеством множества M если 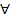 x
x  K x
K x 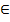 M.
M.
Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком.
U = {Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон}
Равными называют два множества А и В, состоящие из одинаковых элементов: А=В.
Например, равны множества решений уравнений 4x-8=16, x/15=2/5 и 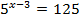 , т.к. их решением будет являться одно и то же число 6.
, т.к. их решением будет являться одно и то же число 6.
Множество не содержащее элементы, которое обладают данным признаком, называется пустым, обозначается  .
.
Мощность – число элементов множества А, обозначается |А| или n(A).
|U| = 9
|  |=0
|=0
11.
Множества.
Операции над множествами
A = {1, 2, 3, 4, 6}
B = {1, 3, 5, 7}
Существуют 4 вида операций:
1) Пересечение множеств

 = {1;3}
= {1;3}
2) Объединение множеств

 = {1; 2; 3; 4; 5; 6; 7}
= {1; 2; 3; 4; 5; 6; 7}
3) Разность множеств А и В состоит из тех элементов, которые принадлежат первому и не принадлежат второму.


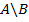 = {2; 4; 6}
= {2; 4; 6}
 = {5; 7}
= {5; 7}
4) Симметрическая разность состоит из тех элементов, которые принадлежат ровно одному из множеств и не принадлежат обоим множествам одновременно.


 = {2; 4; 6}
= {2; 4; 6}  {5; 7}={2; 4; 5; 6; 7}
{5; 7}={2; 4; 5; 6; 7}

12.
Отображения, виды отображений.
Композиция отображений
Пусть даны 2 множества:


Тогда пары  задают соответствие между множествами А и В если указано правило R, по которому для элемента
задают соответствие между множествами А и В если указано правило R, по которому для элемента  из множества
из множества  выбирается элемент
выбирается элемент 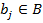 .
.
Пусть задано соответствие R между множествами А и В. Для некоторого элемента a 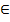 A поставлен в соответствие элемент b
A поставлен в соответствие элемент b 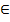 В, который называется образом элемента а и записывается b=R(a).
В, который называется образом элемента а и записывается b=R(a).
Тогда элемент a=  называется прообразом элемента b.
называется прообразом элемента b.
A – множество парабол;
B – множество точек плоскости;
R – соответствие «вершина параболы»;
R(a) – точка, являющаяся вершиной параболы a;
 - состоит из всех парабол
- состоит из всех парабол  с вершиной в точке b.
с вершиной в точке b.
Образ множества A при соответствии R называется множеством значений данного соответствия и обозначается R(A), или R(A) состоит из образов всех элементов множества A. Прообраз множества B при некотором соответствии R называется областью определения этого соответствия и обозначается  .
.
Задание отображений
Композиция отображений.
Пусть даны отображения
 и
и 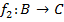 ,
,
тогда отображение

называется композицией отображений  и
и 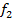
и записывается:


Пример:
f1=Cos(x);
f2=ln(x);
f3=f2  f1=ln(Cos(x))
f1=ln(Cos(x))
f4=f1  f2=Cos(ln(x))
f2=Cos(ln(x))
17.
Индуктивные умозаключения и их виды
Дедукция – от общего к частному.
Индукция – вид умозаключений, при котором на основании анализа частных суждений о принадлежности признака отдельным элементам множества делается вывод о принадлежности этого признака всему множеству.
Оказывается, для проверки индуктивных умозаключений необходимо большое число частных случаев, примеров, опытов, подтверждающих данный вывод. Но для опровержения индуктивного умозаключения достаточно одного контрпримера, противоречащей инстанции.

Виды индукции
| Вид | Вывод | Заключение | Примеры |
| Полная | Достоверный | Перечисление всех элементов | · Метод Сократа.
· «Майевтика» - рождение истины из логической цепочки частных вопросов и ответов, единичных примеров обыденной жизни.
· Индукция через простое перечисление всех элементов конечного счетного множества (перекличка, проверка каталога, перепись жильцов дома и т.д.).
·  есть P; { есть P; {  , ,  ,…, ,…,  } исчерпывает весь класс P; } исчерпывает весь класс P;  есть P. Значит, все элементы S есть P. есть P. Значит, все элементы S есть P.
|
| Математическая | · Формулы общего члена и суммы арифметической (  ) и геометрической ( ) и геометрической (  ) прогрессии.
· Бином Ньютона ) прогрессии.
· Бином Ньютона  .
· Формулы, определенные на множестве N. .
· Формулы, определенные на множестве N.
| ||
| Неполная | Научная | · Законы природы в естественных науках физике, химии, биологии. · Законы развития общества в общественных науках. · Законы логики и философии. | |
| Вероятный | Популярная | · Народные суеверия и приметы.
· Неполная математическая индукция { 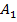 , ,  , ,  ,…, ,…,  ,…}, ,…},
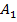 имеет признак B, имеет признак B,
 имеет признак B, имеет признак B,
 имеет признак B.
По-видимому, все А имеют признак В. имеет признак B.
По-видимому, все А имеют признак В.
| |
| Выборка | · Математическая статистика (средняя урожайность, проверка на качество в промышленности, медицина). · Социологические исследования. |
18.
Метод математической индукции
ММИ заключается в следующем:
1) Утверждение проверяется для некоторого начального элемента (например, n=1).
2) Формулируется гипотеза о том, что утверждение справедливо для некоторого натурального k.
3) Доказывается, что если из того, что утверждение справедливо для произвольного k следует, что утверждение справедливо для k+1, то оно справедливо для любого натурального n.
ММИ чаще всего применяется к натуральным числам и с четным множеством для доказательства формул, неравенств, делимости натуральных чисел.
Если равенство не удалось доказать с помощью ММИ, то это не означает, что оно не верное, нужно пробовать другой метод или найти контрпример.
19.
Неориентированные графы. Понятие и основные определения. Теорема о сумме степеней вершин графа. Формула количества ребер в полном графе
Графы.
Графом G=(V,X) называется пара двух конечных множеств: множество точек и множество линий, соединяющих некоторые пары точек. Точки называются вершинами,или узлами, графа, линии – ребрами графа.
Если ребро графа G соединяет две его вершины V и W (т.е. < V, W> 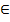 X), то говорят, что
X), то говорят, что
это ребро им инцидентно. Две вершины графа называются смежными, если существует
инцидентное им ребро: рисунок 2.1,а смежными являются вершины А и В, А и С. Если
граф G имеет ребро Х (V,V), у которого начало и конец совпадают , то это ребро
называется петлей. На рис. 2.1,г петля Q (С,С). Два ребра называются смежными, если
они имеют общую вершину.
Граф G(V,X) может иметь ребра с одинаковыми парами вида Х (V,W). Такие ребра называются кратными или параллельными. Количество одинаковых пар вида Х (V,W) называется кратностью ребра (V,W). Число ребер, инцидентных вершине А, называется степенью этой вершины и обозначается deg(A).
Вершина графа, имеющая степень, равную 0, называется изолированной. Граф, состоящий из изолированных вершин, называется 0-графом. Вершина графа, имеющая степень, равную 1, называется висячей.
Теорема 2.1.
В графе G(V,X) сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа: __________ , где n=|V | - это число вершин; m=|X| - число ребер графа.
Вершина называется четной (нечетной),если ее степень – четное (нечетное)число.
Теорема 2.2.
Число нечетных вершин любого графа – четно. Следствие: невозможно начертить граф с нечетным числом нечетных вершин.
Граф G называется полным, если любые две его различные вершины соединены одним и только одним ребром. Дополнением графа G(V,X) называется граф _____________ с теми же вершинами V, что и граф G, и имеющий те и только те ребра Х’, которые необходимо добавить графу G, чтобы он стал полным.
20.
Ориентированные графы. Понятия и основные определения. Понятие расстояния между вершинами в графе. Понятие двудольного графа. Понятие полного двудольного графа.
Если все пары (______) во множестве Х являются упорядоченными, т.е. кортежами длины 2, то граф называется ориентированным, орграфом, или направленным.
Началом ребра называется вершина, указанная в кортеже к первой, концом – вторая вершина этой пары (графически она указана стрелкой).
Ребра орграфа имеют определенные фиксированные начало и конец и называются дугами.
Степенью входа (выхода) вершины орграфа называется число ребер, для которых эта вершина является концом (началом).
Дуги орграфа называются кратными, если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления.
Последовательность попарно инцидентных вершин ____________ неориентированного графа, т.е. последовательность ребер неориентированного графа, в которой вторая вершина предыдущего ребра совпадает с первой вершиной следующего, называется маршрутом. Число ребер маршрута называется длиной маршрута. Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутым или циклом.
Расстояние между двумя вершинами называется минимальная длина из всех возможных маршрутов между этими вершинами, при условии, что существует хотя бы один такой маршрут._____________
Если ребро встретилось только один раз, то маршрут называется цепью.
В орграфе маршрут является ориентированным и называется путем. На путь сразу налагаются важные требования, являющиеся частью определения:
· направление каждой дуги должно совпадать с направлением пути;
· ни одно ребро пути не должно встречаться дважды.
Путь – это упорядоченная последовательность ребер орграфа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны.
Цикл в орграфе – путь, у которого совпадают начало и конец.
Цепь, путь и цикл в графе называются простыми, если они проходят через любую из вершин не более одного раза. Неориентированный граф называется связным, если между любыми двумя его вершинами есть маршрут. Для связанного графа ориентация дуг необязательна.
Ребро (V,W) связного графа G называется мостом, если после его удаления G станет несвязым и распадется на два связных графа G’ и G”.
Теорема Эйлера.
Связный плоский граф с n-вершинами и m-ребрами разбивает плоскость на r-областей (включая внешнюю), причем n-m+r=2.
Граф называется двудольным, если его вершины разбиты на два непересекающихся подмножества _________, а ребра связывают вершины только из разных классов (необязательно все пары). Если каждая вершина множества  cвязана ребром с каждой вершиной множества
cвязана ребром с каждой вершиной множества  , то двудольный граф называется полным двудольным и обозначается
, то двудольный граф называется полным двудольным и обозначается  , где m=|
, где m=|  | и n= |
| и n= |  |.
|.
|
из
5.00
|
Обсуждение в статье: Композиция отображений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

