 |
Главная |
Уравнения в полных дифференциалах
|
из
5.00
|
Раздел1
Частные производные ФНП
1. Найти значения выражения 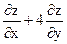 в точке М(1;1), если
в точке М(1;1), если 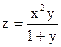 .
.
B) 2
2. Найти значения выражения 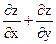 в точке М(2;2), если
в точке М(2;2), если 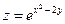 .
.
A) 2
3. Найти значения выражения 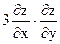 в точке М(2;1), если
в точке М(2;1), если 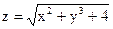 .
.
B) 1
4. Найти значения выражения 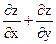 в точке М(2;1), если
в точке М(2;1), если 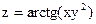 .
.
D) 1
5. Найти значения выражения  в точке М(2;1), если
в точке М(2;1), если 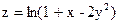 .
.
A) 0
6. Найти значения выражения  в точке М(1;0), если
в точке М(1;0), если  .
.
C) 0
7. Найти значения выражения  в точке М(2;0), если
в точке М(2;0), если 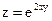 .
.
D) 4
8. Найти значения выражения 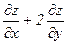 в точке М(1;0), если
в точке М(1;0), если 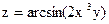 .
.
E) 4
9. Найти значения выражения  в точке М(- 2;0), если
в точке М(- 2;0), если 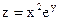 .
.
C) 0
10. Найти значения выражения 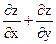 в точке М(0;0), если
в точке М(0;0), если 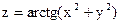 .
.
C) 0
11. Найти значения выражения 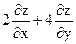 в точке М(1;1), если
в точке М(1;1), если 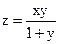 .
.
A) 1
B) 2
12. Найти значения выражения 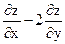 в точке М(3;1), если
в точке М(3;1), если 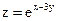 .
.
B) 7
13. Найти значения выражения 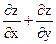 в точке М(2;0), если
в точке М(2;0), если  .
.
B) 1
14. Найти значения выражения  в точке М(0;0), если
в точке М(0;0), если  .
.
A) 4
15. Найти значения выражения 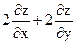 в точке М(1;0), если
в точке М(1;0), если 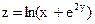 .
.
E) 3
16. Найти значения выражения 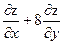 в точке М(1;4), если
в точке М(1;4), если 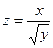 .
.
B) 0
17. Найти значения выражения  в точке М(1;0), если
в точке М(1;0), если  .
.
B) -4,5
18. Найти значения выражения  в точке М(1;0), если
в точке М(1;0), если  .
.
A) -3
19. Найти значения выражения  в точке М(1;1), если
в точке М(1;1), если  .
.
A) 2
20. Найти значения выражения  в точке М(0;1), если
в точке М(0;1), если  .
.
B) -3
21. Найти значения выражения 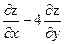 в точке М(1;4), если
в точке М(1;4), если  .
.
E) 3
22. Найти значения выражения 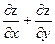 в точке М(1;1), если
в точке М(1;1), если  .
.
C) 48
23. Найти значения выражения 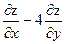 в точке М(0;1), если
в точке М(0;1), если  .
.
A) -7
24. Найти значения выражения  в точке М(0;1), если
в точке М(0;1), если 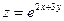 .
.
C) -е3
25. Найти значения выражения 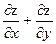 в точке М(1;0), если
в точке М(1;0), если  .
.
D) -6
Раздел2
Экстремум ФНП
1. Найти экстремум функции z = x2 + xy + y2 - 3x – 6у
C) zmin = - 9
2. Найти экстремум функции z = 2х + у - x2 - xy - y2
A) zmax = 1
3. Найти экстремум функции z = 1 - 12х + 2у - 6x2 - y2
C) zmax = 8
4. Найти экстремум функции z = x2 - xy + y2 + 3x +1
A) zmin = -2
5. Найти экстремум функции z = 2ху - 5x2 - 3y2 + 2
D) zmax = 2
6. Найти экстремум функции z = x2 + xy + y2 – 6x – 1.
B) z min = - 13
7. Найти экстремум функции z = x2 - xy + y2 + x + у + 2.
B) zmin = 1
8. Найти экстремум функции z = 1 - 2x2 - xy -2y2 + 15x
C) zmax = 31
9. Найти экстремум функции z = ху - x2 - y2 - 9х + 6у - 5
A) zmax = 16
10. Найти экстремум функции z = x2 + xy + y2 – 2x – у +3
A) zmin = 2
11. Найти экстремум функции z = x3 + 8y3 – 6xy +5
C) zmin= 4
12. Найти экстремум функции z =1- 15x -2x2 -2y2 – xy
B) zmax = 31
13. Найти экстремум функции z = 1+6x - x2 – y 2 – xy -8
B) zmax = 5
14. Найти экстремум функции z = x2 + y2 + 6xy + 22x + 2y +1
C) нет экстремума
15. Найти экстремум функции z = 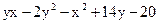
B) zmax = 8
16. Найти экстремум функции z = 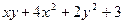
A) zmin = 3
17. Найти экстремум функции z = 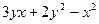
C) нет экстремума
18. Найти экстремум функции z = 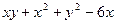
A) zmin =-12
19. Найти экстремум функции z = 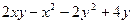
D) zmax = 4
20. Найти экстремум функции z = 
A) zmin =-60
21. Найти экстремум функции z = 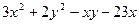
A) zmin =-46
22. Найти экстремум функции z = 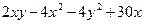
D) zmax = 60
23. Найти экстремум функции z = 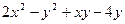
C) нет экстремума
24. Найти экстремум функции z = 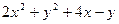
A) zmin =-2,25
25. Найти экстремум функции z = 
C) нет экстремума
| B | A | B | D | A | C | D | E | C | C | B | B | B | A | E | B | B | A | A | B | E | C | A | C | D |
| C | A | C | A | D | B | B | C | A | A | C | B | B | C | B | A | C | A | D | A | A | D | C | A | C |
Раздел3
1. Вычислить 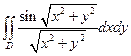 , где D: окружность
, где D: окружность 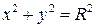
A)  Отв
Отв
2. Вычислить 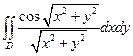 , где D: окружность
, где D: окружность 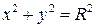
A) 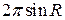 отв
отв
3. Вычислить 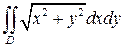 , где D: окружность
, где D: окружность 
А) 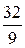 отв
отв
4. Вычислить, перейдя к полярным координатам 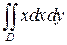 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 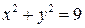 , y=x, y=0
, y=x, y=0
A)  отв
отв
5.Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной линиями 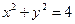 , x=0, y=x
, x=0, y=x
B) 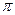 отв
отв
6. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной линиями 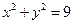 , y=0, y=x
, y=0, y=x
C) 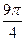 отв
отв
7. Вычислить, перейдя к полярным координатам 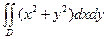 , где D – область половина круга радиуса R с центром в начале координат, лежащая в области y
, где D – область половина круга радиуса R с центром в начале координат, лежащая в области y 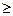 0
0
A)  отв
отв
8.Вычислить, перейдя к полярным координатам 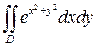 , где D – область четверть круга
, где D – область четверть круга 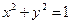 , расположенная в І квадранте.
, расположенная в І квадранте.
A) 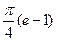 отв
отв

9. Вычислить, перейдя к полярным координатам 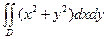 , где D – круг радиуса R с центром в начале координат. Ответа пр.нет
, где D – круг радиуса R с центром в начале координат. Ответа пр.нет
A) 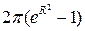 B)
B)  C)
C)  D)
D)  E) 0
E) 0
10.Вычислить, перейдя к полярным координатам  , где D – круг
, где D – круг 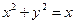
A) 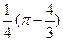 B)
B) 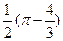 C)
C) 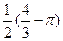 D)
D) 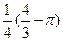 E)
E) 
11.Вычислить, перейдя к полярным координатам 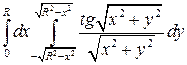
C)  отв
отв
12. Вычислить, перейдя к полярным координатам 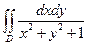 , если область D ограничена полуокружностью
, если область D ограничена полуокружностью 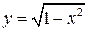 и осью Ох
и осью Ох
A) 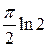 отв
отв
13. Вычислить, переходя к полярным координатам 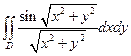 , если область D ограничена линиями
, если область D ограничена линиями 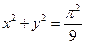 ,
, 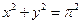
A) 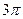 отв
отв
14. Вычислить, переходя к полярным координатам  , если область D ограничена линиями
, если область D ограничена линиями 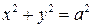 ,
, 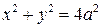
B)  отв
отв
15.Вычислить, переходя к полярным координатам 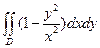 , если область D – круг
, если область D – круг 
A) 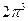 B)
B)  C)
C) 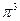
16. Вычислить, переходя к полярным координатам 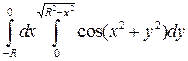
A)  B)
B) 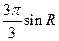 C)
C)  D)
D) 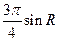 E) 0
E) 0
17. Вычислить двойной интеграл, используя полярные координаты 
A) 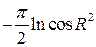 от B)
от B) 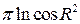 C)
C) 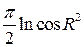 D)
D) 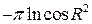 E)
E) 
18. Вычислить двойной интеграл, используя полярные координаты 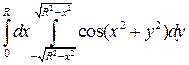
A) 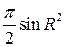 отв
отв
19.Вычислить двойной интеграл, используя полярные координаты 
A) 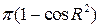 от
от
20. Вычислить двойной интеграл, используя полярные координаты 
A) 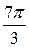 отв
отв
21. Вычислить двойной интеграл, используя полярные координаты 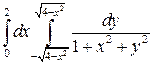
A) 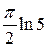 от
от
22. Вычислить двойной интеграл, используя полярные координаты 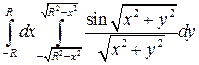
B)  от
от
23. Вычислить двойной интеграл, используя полярные координаты 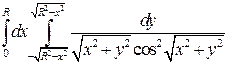
A) 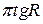 от
от
24.Вычислить двойной интеграл, используя полярные координаты 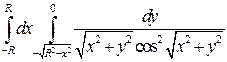
A) 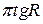 от
от
25. Вычислить двойной интеграл, используя полярные координаты 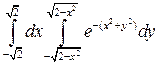
A) 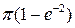 от
от
РАЗДЕЛ 4
Применения кратных интегралов
1. Вычислить объем тела, ограниченного плоскостями  :
:
A) 8
2. Вычислить объем тела, ограниченного плоскостями 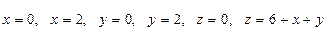
A) 32
3 Вычислить объем тела, ограниченного поверхностью 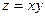 и плоскостями
и плоскостями 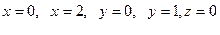 :
:
A) 1
4 Вычислить массу прямоугольной пластинки, ограниченной прямыми 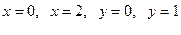 , если ее плотность
, если ее плотность 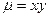 задана:
задана:
A) 1
5 Вычислить массу прямоугольной пластинки, ограниченной прямыми 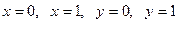 и с если ее плотность
и с если ее плотность 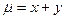 задана:
задана:
A) 1
6 Вычислить объем тела, ограниченного плоскостями 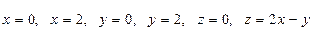
A) 4
7 Вычислить объем тела, ограниченного плоскостями 
A) 24
8 Вычислить объем тела, ограниченного плоскостями 
A) 16
9 Вычислить массу пластинки, ограниченной прямыми 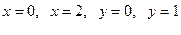 , если ее плотность
, если ее плотность 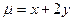 задана:
задана:
A) 4
10 Вычислить массу пластинки, ограниченной прямыми  , если ее плотность
, если ее плотность 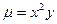 задана:
задана:
A) 18
11 Вычислить объем тела, ограниченного плоскостями 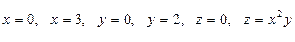
A) 18
12 Вычислить массу пластинки, ограниченной прямыми 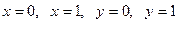 , если плотность задана функцией
, если плотность задана функцией  :
:
A) 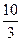
13 Вычислить массу пластинки, ограниченной прямыми 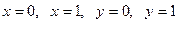 , если ее плотность задана функцией
, если ее плотность задана функцией 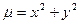 :
:
А) 
14 Вычислить массу пластинки, ограниченной прямыми  , если ее плотность задана функцией
, если ее плотность задана функцией  :
:
A) 8
15 Вычислить объем тела, ограниченного плоскостями 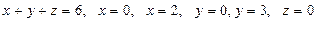 :
:
A) 21
16 Вычислить объем тела, ограниченного поверхностями :  :
:
A) 
17 Вычислить объем тела, ограниченного поверхностями : 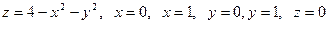
A) 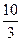
18 Вычислить объем тела, ограниченного плоскостями 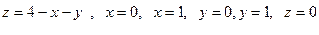
A) 3
19 Вычислить массу пластинки, ограниченной прямыми  , если ее плотность задана функцией
, если ее плотность задана функцией 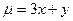 :
:
A) 16
B) 20 Вычислить массу пластинки, ограниченной прямыми 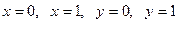 , если ее плотность задана функцией
, если ее плотность задана функцией 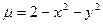 :
:
A) 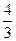
21 Вычислить массу пластинки, ограниченной прямыми 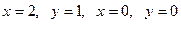 , если ее плотность задана функцией
, если ее плотность задана функцией 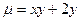 :
:
A) 3
22 Вычислить массу пластинки, ограниченной прямыми 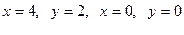 , если ее плотность задана функцией
, если ее плотность задана функцией 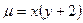 :
:
A) 48
23 Вычислить массу пластинки, ограниченной кривыми 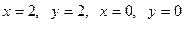 , если ее плотность задана функцией
, если ее плотность задана функцией 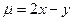 :
:
A) 4
24 Вычислить объем тела, ограниченного плоскостями 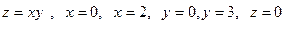
A) 9
25 Вычислить объем тела, ограниченного поверхностями : 
A) 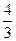
РАЗДЕЛ 5
1. В 10 экзаменационных билетах содержится по два вопроса, которые не повторяются. Студент знает ответы только на 16 вопросов. Какова вероятность того, что доставшийся студенту билет содержит известные ему вопросы?
A) 
2. В бригаде пять мужчин и три женщины. По списку отобраны два человека. Найти вероятность того, что все отобранные лица окажутся женщинами.
D) 
3. Две концентрические окружности радиуса 12 см и 7 см образуют кольцо. Какова вероятность того, что точка помещаемая наудачу в большой круг попадет в кольцо.
A) 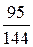
4. В мастерскую для ремонта поступили 9 приборов. Четыре из них требуют капитального ремонта. Мастер берет наудачу два прибора. Найти вероятность того, что один из взятых приборов требует капитального ремонта.
A) 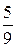
5. В круг радиуса 8 см вписан квадрат. Чему равна вероятность того, что точка помещаемая наудачу в круг, попадет и в квадрат?
A) 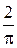
6. В урне 3 красных и 4 белых шара. Наудачу отобраны два шара. Найти вероятность того, что отобраны один красный, один белый шар.
A) 
7. В урне 3 красных и 4 белых шара. Из урны извлечена один шар. Шар возвращают в урну и вторично из той же урны наудачу извлекают один шар. Найти вероятность того, что оба раза извлечены белые шары.
A) 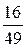
8. На бесконечную шахматную доску, сторона каждой клетки которой равна 15 см, бросают монету радиуса 6 см. Найти вероятность того, что монета попадет целиком внутрь одной клетки.
A) 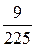
9. В двух партиях 71% и 47% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них хотя бы одно бракованное.
A) 0,6663
10. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; для второго и третьего стрелков эти вероятности соответственно равны 0,8 и 0,9. Найти вероятности того, что только один из стрелков поразит цель.
A) 0,092
11. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; для второго и третьего стрелков эти вероятности соответственно равны 0,8 и 0,9. Найти вероятности того, что хотя бы один из стрелков поразит цель.
A) 0,994
12. Вероятность того, что цель поражена первым стрелком равна 0,7; вторым 0,6. Первый сделал два, второй один выстрел. Найти вероятность того, что цель не поражена.
A) 0,036
В лифт восьми этажного дома сели три пассажира. Каждый независимо от других может выйти на любом (начиная со второго) этаже. Найти вероятность того, что все вышли на разных этажах.
A) 
14. Закон распределения дискретной случайной величины X имеет вид:
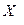
| –1 | y |

| 0.4 | 0.6 |
Математическое ожидание 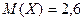 . Найти y.
. Найти y.
E)5
15. Найти математическое ожидание М(Х) дискретной случайной величины Х, заданной законом распределения:
| х | -2 | ||
| р | 0,32 | 0,21 | 0,47 |
A) М(X) = 0,98
16. Найти математическое ожидание М(Х) дискретной случайной величины Х, заданной законом распределения:
| х | -3 | -2 | |
| р | 0,21 | 0,43 | 0,36 |
B) М(X) = -1,13
17. Найти математическое ожидание М(Х) дискретной случайной величины Х, заданной законом распределения
| х | -2 | ||
| р | 0,12 | 0,23 | 0,65 |
C) М(X) = 1,94
18. Найти математическое ожидание М(Х) дискретной случайной величины Х, заданной законом распределения
| х | -3 | -1 | |
| р | 0,42 | 0,53 | 0,05 |
D) М(X) = - 1,69
19. Найти математическое ожидание М(Х) дискретной случайной величины Х, заданной законом распределения:
| х | -2 | ||
| р | 0,21 | 0,5 | 0,29 |
E) М(X) = 1,45
20. Найти математическое ожидание М(Х) случайной величины 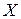 , зная закон её распределения:
, зная закон её распределения:
| X | |||
| p | 0,1 | 0,6 | 0,3 |
A) 
21. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z=3X+2Y, если известно, что D(X)=5, D(Y)=6.
A) 69
22. Найти дисперсию случайной величины 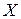 , которая задана следующим законом распределения:
, которая задана следующим законом распределения:
| X | |||
| p | 0,3 | 0,5 | 0,2 |
A) 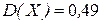
23. Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию  случайной величины
случайной величины 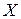 – числа появлений события в этих испытаниях.
– числа появлений события в этих испытаниях.
A) 
24. Найти дисперсию дискретной случайной величины Х заданной законом распределения
| X | |||
| p | 0,2 | 0,3 | 0,5 |
A) 3,64
25. Найти дисперсию  случайной величины
случайной величины 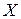 , которая задана следующим законом распределения:
, которая задана следующим законом распределения:
| X | |||
| p | 0,3 | 0,5 | 0,2 |
A) 
РАЗДЕЛ 6
1. Найти частное решение уравнения 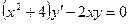 ,
, 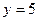 , при
, при 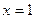
A) 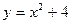
2. Найти частное решение уравнения 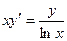 ,
, 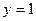 , при
, при 
A) 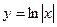
3. Найти частное решение уравнения  ,
, 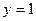 , при
, при 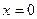
A) 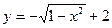
4. Найти частное решение уравнения 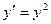 ,
, 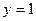 , при
, при 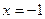
A) 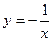
5. Найти частное решение уравнения 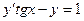 ,
, 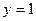 , при
, при 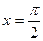
A) 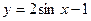
6. Найти частное решение уравнения 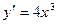 ,
, 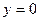 , при
, при 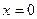
A) 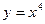
7. Найти частное решение уравнения 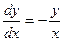 ,
,  , при
, при 
A) 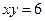
8. 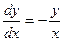 , найти интегральную кривую, проходящую через точку
, найти интегральную кривую, проходящую через точку 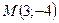
A) 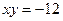
9. Найти общее решение 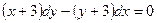

A) 
10. Найти общее решение 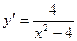
A) 
11. Найти общее решение 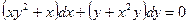
A) 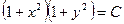
12. Найти общее решение 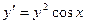
A) 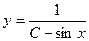
13. Найти общее решение 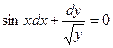
A) 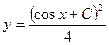
14. Найти общее решение 
A) 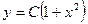
15. Найти общий интеграл 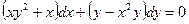
A) 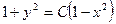
16. Найти общий интеграл 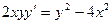
A) 
17. Найти общий интеграл 
A) 
18. Найти общий интеграл 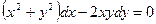
A) 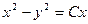
19. Найти общее решение 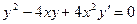
A) 
20. Найти общий интеграл 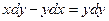
A) 
21. Найти общий интеграл 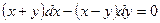
A) 
22. Найти общий интеграл 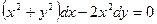
A) 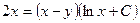
23. Найти общий интеграл 
A) 
24. Найти общий интеграл 
A) 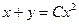
25. Найти общее решение 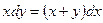
A) 
1. Найти общее решение 
A) 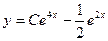
2. Найти общее решение 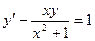
A) 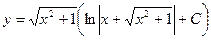
3. Найти общее решение 
A) 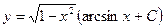
4. Найти общее решение 
A) 
5. Найти общее решение 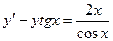
A) 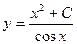
6. Найти общее решение 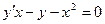
A) 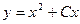
7. Найти общее решение 
A) 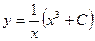
8. Найти общее решение 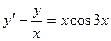
A) 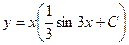
9. Найти общее решение 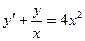
A) 
10. Найти общее решение 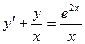
A) 
11. Найти общее решение 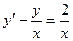
A) 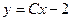
12. Найти общее решение 
A) 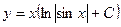
13. Найти общее решение 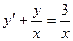
A) 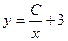
14. Найти общее решение 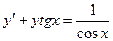
A) 
15. Найти общее решение 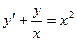
A) 
16. Найти общее решение 
A) 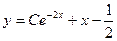
17. Найти общее решение 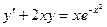
A) 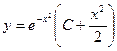
18. Найти общее решение 
A) 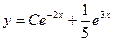
19. Найти общее решение 
A) 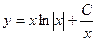
20. Найти общее решение 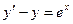
A) 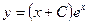
21. Найти общее решение 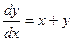
A) 
B) 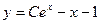
C) 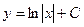
D) 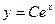
E) 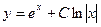
22. Найти общее решение 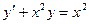
A) 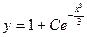
23. Найти общее решение 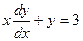
A) 
24. Найти общее решение 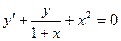
A) 
25. Найти общее решение 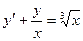
A) 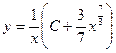
РАЗДЕЛ 7
Уравнения в полных дифференциалах
1. Найти частный интеграл уравнения  удовлетворяющий начальному условию
удовлетворяющий начальному условию 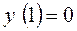 :
:
А) 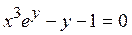
2. Найти частный интеграл уравнения 
удовлетворяющий начальному условию 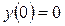 :
:
A) 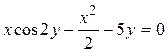
3. Найти частный интеграл уравнения 
удовлетворяющий начальному условию 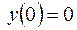 .
.
A) 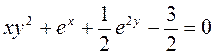
4. Найти частный интеграл уравнения 
удовлетворяющий начальному условию 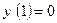 .
.
A) 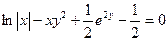
5. Найти частный интеграл уравнения 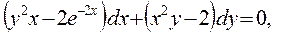
удовлетворяющий начальному условию  :
:
A) 
6. Найти частный интеграл уравнения 
удовлетворяющий начальному условию 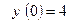 :
:
A) 
7. Найти частный интеграл уравнения 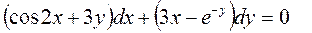
удовлетворяющий начальному условию


