 |
Главная |
Теорема 2. О непрерывности композиции функций
|
из
5.00
|
Определение 2
 Окрестность
Окрестность  называют проколотой, если из
называют проколотой, если из  исключена сама точка
исключена сама точка  , и обозначается
, и обозначается  (или
(или  ).
).
Определение 3
Говорят, что функция  имеет в точке
имеет в точке  предел, равный
предел, равный  , если для любой последовательности точек
, если для любой последовательности точек  , сходящейся к точке
, сходящейся к точке  , последовательность значений
, последовательность значений  сходится к числу
сходится к числу  и обозначается
и обозначается 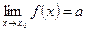 .
.
Замечание 1
Функция  может быть не определена в самой точке
может быть не определена в самой точке  .
.
Замечание 2
Так как предел функции есть более сложноорганизованный предел последовательно-сти, то имеют место все теоремы о пределах последовательностей.
Пример 1
Вычислим  .
.
Выберем любую последовательность  :
:  . Тогда
. Тогда 
 .
.
Пример 2
Вычислим 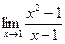 .
.
Выберем любую последовательность  такую, что
такую, что  . Тогда возникает неопределенность
. Тогда возникает неопределенность 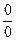 . Воспользуемся тем, что для любого
. Воспользуемся тем, что для любого  . Тогда
. Тогда  .
.
Пример 3
Рассмотрим функцию Дирихле  , (
, (  - множество рациональных чисел).
- множество рациональных чисел).
Если взять последовательность  , где
, где  , то
, то  ; если же
; если же  такова, что
такова, что  , то
, то  . Значит, функция Дирихле не имеет предел ни в одной точке действительной оси, так значение предела зависит от выбора последовательности
. Значит, функция Дирихле не имеет предел ни в одной точке действительной оси, так значение предела зависит от выбора последовательности  .
.
Теорема 1. Критерий Коши существования предела.
Для любого  , найдется
, найдется  , зависящее от
, зависящее от  , такое что
, такое что  ,следовательно
,следовательно  , что равносильно:
, что равносильно: 
 (1)
(1)
Доказательство:
Необходимость.Пусть соотношение (1) выполняется. Покажем, что для любой последовательности  , последовательность
, последовательность  стремится к
стремится к  при
при  . Выберем какое-нибудь
. Выберем какое-нибудь  . По
. По  найдем
найдем  из неравенства
из неравенства  , т.е. определим окрестность
, т.е. определим окрестность  . Зная
. Зная  , можно найти номер
, можно найти номер  , начиная с которого
, начиная с которого  попадает в
попадает в 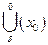 (
(  - коридор точки
- коридор точки  ). Тогда в силу соотношения (1) имеем
). Тогда в силу соотношения (1) имеем  . Это означает, что выполняется соотношение (**) для последовательности
. Это означает, что выполняется соотношение (**) для последовательности  , т.е.
, т.е.  .
.
Достаточность.Пусть существует 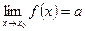 . Покажем, что выполняется соотношение (1). Воспользуемся методом от противного.
. Покажем, что выполняется соотношение (1). Воспользуемся методом от противного.
Пусть соотношение (1) не выполняется, т.е.  .
.
Так как  , то выполняется соотношение (**), т.е. найдется номер
, то выполняется соотношение (**), т.е. найдется номер  , начиная с которого
, начиная с которого 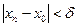 . Так как
. Так как  любое, то выберем в качестве
любое, то выберем в качестве  . Тогда
. Тогда  . По теореме о «двух милиционерах» при
. По теореме о «двух милиционерах» при 
 . Но тогда в силу определения 2 последовательность
. Но тогда в силу определения 2 последовательность  , т.е.
, т.е.  (имеет место соотношение (**)). Получили противоречие.
(имеет место соотношение (**)). Получили противоречие.
Определение 4.
Определение по Коши
Говорят, что функция  имеет в точке
имеет в точке  предел, равный
предел, равный  , если
, если 
 , т.е. выполняется соотношение (1).
, т.е. выполняется соотношение (1).
Замечание 3
Сформулируем определение предела функ-ции  в точке
в точке  на языке окрестностей:
на языке окрестностей:

 (
(  - окрестность точки
- окрестность точки  );
);
или
 .
.
Пример 4
Докажем, что  .
.
Так как  , то для любого
, то для любого  выберем
выберем  . При этом для всех
. При этом для всех  таких, что
таких, что  получим
получим 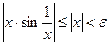 . Таким образом,
. Таким образом, 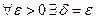
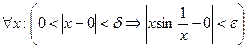 , т.е.
, т.е.  .
.
Пример 5
Докажем, что не существует предела функции
 в точке
в точке 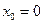 .
.
Рассмотрим последовательности 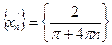 и
и  . При
. При 
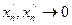 , но
, но  . Значит,
. Значит,  .
.
Определение 5
Число  называется пределом функции
называется пределом функции  в точке
в точке  слева, если
слева, если 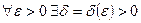
 . При этом число
. При этом число 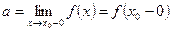 называют левым пределом функции
называют левым пределом функции  в точке
в точке  .
.
Аналогично вводится понятие правого предела  функции
функции  в точке
в точке  .
.
Теорема 2
Для того, чтобы существовал предел 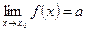 , необходимо и достаточно, чтобы в точке
, необходимо и достаточно, чтобы в точке  существовали односторонние пределы
существовали односторонние пределы  , причем
, причем  .
.
Доказательство:
Необходимость.Пусть существует 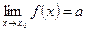 , т.е.
, т.е.  . Выберем последовательность
. Выберем последовательность  такой, что
такой, что  . Тогда получаем существование
. Тогда получаем существование 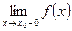 , причем
, причем 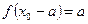 .
.
Для доказательства существования  достаточно выбрать любую последовательность
достаточно выбрать любую последовательность  , такую, что
, такую, что  .
.
Достаточность.Пусть существует  , т.е.
, т.е.  ,
,  .
.
Выберем  . Тогда для любого
. Тогда для любого 
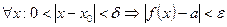 . +
. +
п. 2 Замечательные пределы
1. Первый замечательный предел  .
.
 Доказательство:
Доказательство:
| рис .6.3 |
Рассмотрим единичную окружность. Пусть  . Тогда
. Тогда  . Из рисунка видно, что
. Из рисунка видно, что  ,
,
 ,
,  . Тогда
. Тогда 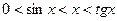 .
.
Так как  , то
, то  . В силу того, что
. В силу того, что  , получим
, получим  . Это неравенство имеет место и для
. Это неравенство имеет место и для  , т.к. функции
, т.к. функции 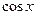 и
и 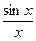 четные. Легко показать, что
четные. Легко показать, что  . +
. +
Следствия
1. 
2. 
3. 
4.  (
(  )
)
5. 
Доказательство (5):
 .
.
2. Второй замечательный предел  .
.
Доказательство:
Пусть  . Положим
. Положим  . Тогда
. Тогда 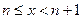 или
или  . Имеет место неравенство
. Имеет место неравенство  . Так как
. Так как  , то
, то 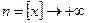 . Из неравенства
. Из неравенства  в силу того, что
в силу того, что  и
и  имеем
имеем  .
.
Теперь пусть  . Положим
. Положим  . Теперь
. Теперь  . Тогда
. Тогда 
 . +
. +
Следствия
1. 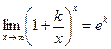 .
.
2. 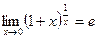 .
.
3,  в частности,
в частности,  .
.
4.  , в частности
, в частности  .
.
Доказательство (4):

 . +
. +
5. 
Доказательство (5):

 . +
. +
п. 3 Непрерывность функции в точке
Определение 1Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности 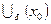 точки
точки  . Говорят, что функция
. Говорят, что функция  непрерывна в точке
непрерывна в точке  , если выполняется соотношение
, если выполняется соотношение  .
.
Определение 2
Функция  непрерывна в точке
непрерывна в точке  , если
, если  .
.
Определение 2*
Функция  непрерывна в точке
непрерывна в точке  , если
, если  .
.
Определение 3
Функция  называется бесконечно малойв точке
называется бесконечно малойв точке  , если
, если  .
.
Определение 4
Функция  называется непрерывнойв точке
называется непрерывнойв точке  , если бесконечно малому приращению
, если бесконечно малому приращению  аргумента соответствует бесконечно малое приращение
аргумента соответствует бесконечно малое приращение  функции, т.е.
функции, т.е.  , где
, где  .
.
Свойства непрерывных функций в точке
Теорема 1
Пусть функции  непрерывны в точке
непрерывны в точке  . Тогда
. Тогда  непрерывны в точке
непрерывны в точке  .
.
Доказательство:
Докажем непрерывность произведения  в точке
в точке  . Так как функции
. Так как функции  и
и  непрерывны в точке
непрерывны в точке  , то можно представить
, то можно представить  , где
, где  - БМФ в точке
- БМФ в точке  . Тогда
. Тогда 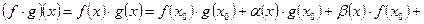
 . Перейдем к пределу при
. Перейдем к пределу при 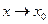 . Получим
. Получим  .
.
Определение 5
Пусть функция  определена в некото-
определена в некото-
рой окрестности точки  , а
, а  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Тогда функция
. Тогда функция  называется композицией функции или сложной функцией, а операция образования
называется композицией функции или сложной функцией, а операция образования  называется операцией композиции.
называется операцией композиции.
Замечание 1
Так как  , то
, то  , т.е. для непрерывной функции знак функции и предела можно менять местами.
, т.е. для непрерывной функции знак функции и предела можно менять местами.
Теорема 2. О непрерывности композиции функций
Пусть функция  непрерывна в точке
непрерывна в точке  ; функция
; функция  непрерывна в точке
непрерывна в точке  , причем
, причем  . Тогда
. Тогда  непрерывна в точке
непрерывна в точке  .
.
Доказательство:
По условию  . Рассмотрим
. Рассмотрим 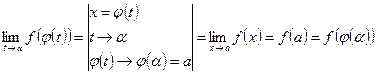 .
.
Определение 6
Функции  назы-
назы-
вают основными элементарными функциями. Функции, полученные из основных элементарных с помощью арифметических операций и операции композиции называются элементарными.
Теорема 3
Любая элементарная функция непрерывна на своей области определения.
Пример 1
Покажем непрерывность  в любой точке
в любой точке  числовой оси.
числовой оси.
Доказательство:
Рассмотрим  . Тогда
. Тогда  , что значит
, что значит  . Мы воспользовались тем, что
. Мы воспользовались тем, что  . Действительно, если
. Действительно, если  , то
, то  при
при  . Тогда при
. Тогда при  . Если же
. Если же  , то
, то  .
.
Определение 7
Точка  , в окрестности которой определена функция
, в окрестности которой определена функция  , причем в самой точке
, причем в самой точке  может быть не определена, называется точкой разрыва функции
может быть не определена, называется точкой разрыва функции  , если
, если  не является непрерывной в точке
не является непрерывной в точке  .
.
Точки разрыва функции бывают:
- точкой устранимого разрыва, если существуют  , причем
, причем  ;
;
- точкой разрыва I рода, если существуют  , но
, но 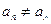 ;
;
- точкой разрыва II рода, если хотя бы один из односторонних пределов  или
или 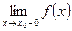 бесконечен или не существует.
бесконечен или не существует.
| рис. 6.4 |
 Пример
Пример
Рассмотрим функцию 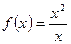 . Данная функция
. Данная функция  определена при
определена при  . В точке
. В точке  функция имеет разрыв. Найдем
функция имеет разрыв. Найдем  и
и  .
.
Тогда, доопределив функцию  в точке
в точке  , получим функцию
, получим функцию  , являющейся непрерывной в точке
, являющейся непрерывной в точке  .
.
Таким образом, мы устранили разрыв. Поэтому точка  является точкой устранимого разрыва функции
является точкой устранимого разрыва функции 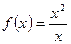 .
.
Пример 2
Рассмотрим функцию 

Каждая составная часть этой функции, кроме последней, непрерывна. Следовательно, надо исследовать функцию на стыках и в точке  . Вычислим все односторонние пределы:
. Вычислим все односторонние пределы:
1)  ;
;
 - точка непрерывности;
- точка непрерывности;
2)  ;
;
 - точка разрыва I
- точка разрыва I
рода;
3) 
 – точка разрыва I рода.
– точка разрыва I рода.
Пример
Рассмотрим функцию  .
.
 |
Функция имеет разрыв только в точке
 . Исследуем его:
. Исследуем его:  . Тогда
. Тогда  - точка разрыва II рода.
- точка разрыва II рода.
| рис. 6.6 |
п. 4 Бесконечно малые функции и их сравнение
Определение 1
Функцию  называют БМФ в окрестности точки
называют БМФ в окрестности точки  , если
, если  .
.
Определение 2
Функцию  называют ББФ в окрестности точки
называют ББФ в окрестности точки  , если
, если  , т.е.
, т.е.  .
.
Если  - БМФ в точке
- БМФ в точке  , то
, то 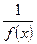 -ББФ в точке
-ББФ в точке  . Например, функция
. Например, функция 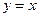 в
в 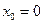 является БМФ, а
является БМФ, а  - ББФ в точке
- ББФ в точке 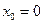 .
.
Определение 3
Пусть  - БМФ в окрестности
- БМФ в окрестности 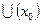 точки
точки  . Тогда:
. Тогда:
-  называют бесконечно малой более высокого порядка малости, чем
называют бесконечно малой более высокого порядка малости, чем  , если
, если 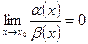 и обозначают
и обозначают  ;
;
-  и
и  называют БМФ одного порядка малости, если
называют БМФ одного порядка малости, если  ;
;
-  и
и  называют эквивалентными,
называют эквивалентными,
если 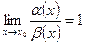 и обозначают
и обозначают  при
при 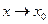 .
.
Теорема 1
Если  при
при 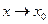 , то
, то 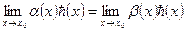 .
.
Доказательство:
Рассмотрим  .
.
Теорема 2
Пусть  при
при 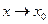 . Тогда их разность
. Тогда их разность  является бесконечно малой большего порядка малости, чем каждая из них, т.е.
является бесконечно малой большего порядка малости, чем каждая из них, т.е.  и
и  при
при 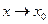 .
.
Доказательство:
Рассмотрим 
 .
.
Аналогично,  . +
. +
Замечание
Полученный результат позволяет все экви-
валентности записать в виде: если  при
при 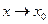 , то
, то  . Например,
. Например, 
 и т.д.
и т.д.
Определение 4
Представление функции  в окрестности
в окрестности 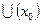 точки
точки  в виде
в виде  , где
, где  - некоторая константа, называется выделением главной части функции, при этом
- некоторая константа, называется выделением главной части функции, при этом  называется главной частьюфункции
называется главной частьюфункции  в
в 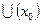 , а
, а  - порядок малостиэтой функции.
- порядок малостиэтой функции.
Пример
Вычислить  . Выделим главные части в каждом слагаемом числителя и знаменателя:
. Выделим главные части в каждом слагаемом числителя и знаменателя:  ,
,  ,
, 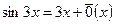 ,
, 
 .
.
Тогда 
п. 5 Свойства функций, непрерывных на промежутке
Определение 1
Функция  непрерывна на отрезке
непрерывна на отрезке  , если она непрерывна в каждой внутренней точке
, если она непрерывна в каждой внутренней точке  , а на концах отрезка непрерывна слева и справа соответственно, т.е.
, а на концах отрезка непрерывна слева и справа соответственно, т.е.  ,
,  .
.
Определение 2
Функция  ограничена сверху (снизу)на промежутке
ограничена сверху (снизу)на промежутке  , если
, если  .
.
Говорят, что функция  ограничена на промежутке
ограничена на промежутке  , если
, если  .
.
Замечание
Пусть  . Тогда
. Тогда  ограничена на
ограничена на  , если
, если  .
.
Определение 3
Говорят, что функция  неограниченна на интервале
неограниченна на интервале  , если
, если  .
.
Определение 4
 - ТВГфункции
- ТВГфункции  на отрезке
на отрезке  , если:
, если:
1)  ;
;
2) 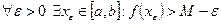 .
.
Определение 5
 - ТНГфункции
- ТНГфункции  на отрезке
на отрезке  , если:
, если:
1)  ;
;
2)  .
.
|
из
5.00
|
Обсуждение в статье: Теорема 2. О непрерывности композиции функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

