Обобщенная дистрибьютивность

Глава I. Теория множеств.

Лекция 1.

 

Понятие множества

Определение. Множество – объединение в единое целое объектов, хорошо различаемых нашей интуицией или мыслью. Объекты, составляющие множество, называются элементами множества. Множества обозначаются большими латинскими буквами (S), элементы множеств – маленькими (x, y).

Обозначения: Элемент принадлежит множеству: x Î S

Элемент не принадлежит множеству: y Ï S

Примеры множеств: N - множество натуральных чисел, Z - множество целых чисел, Q - множество рациональных чисел, R - множество действительных чисел, C - множество комплексных чисел.

 

Определение. Множество называется конечным, если оно содержит конечное число элементов.

 

Определение. Пустое (Æ) множество не содержит элементов.

 

Способы задания множеств:

1) Задание полного списка элементов. H = {понедельник, вторник, … воскресенье}

2) Указание некоторого характерного свойства. H = { x | свойство} H = { x | x = 2n, n Î N}

(иногда известны не все элементы множества)

 

Отношения между множествами:

Определение. Два множества называются равными, если они состоят из одних и тех же элементов.

(А = В) Û ("x Î A, x Î B ^ "x Î B x Î A)

 

Пример. A – множество положительных четных чисел. B – множество натуральных чисел, состоящих из сумм двух положительных нечетных чисел.

Доказательство: Необходимость. Пусть х Î А Þ x = 2n = (2n - 1) + 1 Þ x Î B

Достаточность. "x Î B Þ x = 2p – 1 + 2q – 1 = 2(p + q – 1) Þ х Î А

Следовательно: А = В.

Примеры: {2, 4, 6} = {6, 2, 4} = {4, 4, 2, 6}

Элементами множества могут быть и сами множества:

{студенты на лекции} = {421, 422, …, 426}

{1, 2} ¹ {{1, 2}}

 

Отношение включения.

Определение. Если каждый элемент множества А является элементом множества В, то А Í В (включено), при этом А – подмножество В. Если А Í В ^ А ¹ В, то А Ì В (строго включено).

 

Основные свойства Отношения включения:

1) А Í А

2) (А Í В ^ В Í С) Þ А Í С

3) (А Í В ^ В Í А) Þ А = В

Доказательство 2-го свойства: х Í А Þ х Í В Þ х Í С Следовательно: А Í С.

 

Примеры: А Ì В ^ В Ì С Þ А Ì С А Í В ^ В Ì С Þ А Ì С

 

Сравнимость множеств.

Определение. Множества А и В сравнимые, если А Í В Ú В Í А

 

Пример. A = { x | x > 3}, B = { x | x ³ 1}, C = { x | -5 < x ≤ 2}

A Ì B Þ А и В сравнимы, А и С не сравнимые, В и С не сравнимые.

 

Диаграмма Венна.

Определение. U – универсальное множество для данной задачи, если все рассматриваемые в этой задаче множества являются его подмножествами.

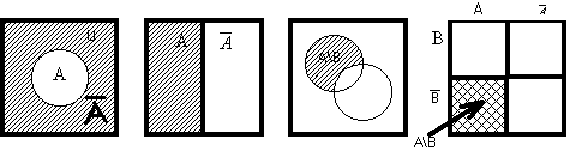
Определение. Диаграммой Венна называется схема множества U в виде прямоугольника, а других множеств в виде кругов или в какой-то другой области.

 

Алгебраические операции над множествами.

Определение. Относительным дополнениеммножества А до множества Х называется Х\А = { x | x Î X ^ x Ï A} (разность Х - А, Х без А).

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат А. = U\A – абсолютное добавление.

Определение. Объединением множеств (А È В) называется множество, элементы которого принадлежат хотя бы одному из этих множеств.

 

Определение. Пересечением множеств (А Ç В) называется множество, элементы которого принадлежат каждому из этих множеств.

 

Определение. Симметрической разностью множеств называется множество, элементы которого принадлежат ровно одному из этих множеств: А Ä В=(А \ В) Ú (В \ А).

 

Законы алгебры множеств.

1) Коммутативность

a) А È В = В È А

b) А Ç В = В Ç А

c) А Ä В = В Ä А

d) А \ В ¹ В \ А

2) Ассоциативность

a) А È (В È С) = (А È В) È С

b) А Ç (В Ç С) = (А Ç В) Ç С

c) А Ä (В Ä С) = (А Ä В) Ä С

d) А \ (В \ С) ¹ (А \ В) \ С

3) Дистрибутивность

a) А Ç (В È С) = (А Ç В) È (А Ç С)

b) А È (В Ç С) = (А È В) Ç (А È С)

4) – без названия

a) А Ç А = А

b) А È А = А

c) А Ç Æ = Æ

d) А È Æ = А

e) А Ç U = А

f) А È U = U

5) Законы де Моргана

a) 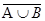= Ç

b) = È

6) Дополнение к U и Æ

a) = Æ

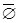b) = U

7) Поглощение

a) А È (А Ç В) = А

b) А Ç (А È В) = А

8) – без названия –

a) Если " А, А È В = А, то В = Æ

b) Если " А, А Ç В = А, то В = U

9) Если А È В = U ^ А Ç В = Æ => В = А =

10) Двойное дополнение: = А

 

Полезные тождества:

1) А È В = А Ä В Ä (А Ç В)

2) А \ В = А Ä (А Ç В)

3) А Ç В = (А È В) Ä А Ä В

4) А \ В = (А È В) Ä В

5) А Ç В = А \ (А \ В)

6) А È В = (А Ä В) Ä (А \ (А \ В))

Нельзя выразить \ через «Ç» и «È»,или «Ç» через «È» и «\»

 

Лекция 2.

Определение. Равенство алгебры множеств, полученное заменой всех знаков È на Ç, Ç на È, U на Æ, Æ на U называется двойственным.

Все рассматриваемые законы алгебры множеств двойственны.

Закон 9 – самодвойственный.

Для разности двойственный закон верен, т.к. А \ В = А Ç

 

Закон дистрибьютивности определения относительно пересечения:

А È (В Ç С) = (А È В) Ç (А È С)

Доказательство:

а) Необходимость: "x Í (A È (B Ç C)) Þ (x Í A Ú x Í B È C);

x ( B ( C Þ (x Í B) ^ (x Í C) Þ (x Í A È B) ^ (x Í A È C) Þ x Í (A È B) È (A È C)

б) Достаточность: "x Í (A È B) È (A È C) Þ (x Í A È B) ^ (x Í A È C) Þ

Þ ((x Í A) Ú (x Í B) ^ (x Í A) Ú (x Í C)) Þ (x Í A) Ú ((x Í B) ^ (x Í C)) Þ x Í А È (В Ç С)

 

Закон де Моргана: 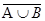= Ç

Доказательство:

а) Необходимость: "x Í 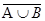Þ x Ï (A È B) Þ (x Ï A) ^ (x Ï B) Þ (x Í ) ^ (x Í ) Þ x Í ( Ç )

б) Достаточность: "x Í ( Ç ) Þ (x Í ) ^ (x Í ) Þ (x Ï A) ^ (x Ï B) Þ x Ï (A È B) Þ x Í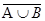

Примеры:

æ A \ B = Æ | A \ B = A Ç = Æ Þ A Í B ü

è B \ A = Æ | Û B \ A = B Ç = Æ Þ B Í A þ Þ A = B

Ýß

A Ä B = Æ Û A = B

 

Утверждение. Отношения включения множеств могут быть определены в терминах È и Ç.

 

Следующие утверждения о произвольных множествах А и В попарно-эквивалентны:

1) А Ç В = А

2) А È В = В A Í B

3) А \ В = Æ

4) А È В = U

5) А Ç В = Æ

 

Примеры:

1) 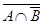È B = ( È ) È B = ( È B) È B = È (B È B) = È B

2) (A \ B) È (A Ç B) = (A Ç ) È (A Ç B) = A Ç ( È B) = A È U = A

 

Обобщенные тождества алгебры множеств:

Обобщенная дистрибьютивность

а) A Ç (B­₁ È B₂ È ... È B_n) = (A Ç B₁) È (A Ç B₂) È ... È (A Ç B_n)

а) A Ç ( ) = (1)

б) A È ( ) =

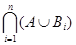
Доказательство утверждения (а): (методом математической индукции)

1) n = 2: левая часть (1) = A Ç (B­₁ È B₂) ü

правая часть (1) = (A Ç B₁) È (A Ç B₂) þ Þ левая часть = правая часть (по доказанному ранее)

2) Допустим A Ç ( ) = 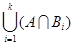, (k Î N, k ³ 2) - верно

Надо доказать: A Ç ( ) =

Доказательство: A Ç ( ) = A Ç ( È B_k+1) = [по доказательству в 1] =

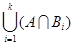= (A Ç ( )) È (A Ç B_k+1) = [по допущению] = È (A Ç B_k+1) =

Так как выполнено оба условия обобщенного принципа математической индукции, то равенство (1) верно.