 |
Главная |
Принцип двойственности
|
из
5.00
|
Определение. Функция f*(x1, …, xn) =  называется двойственной функции f(x1, …, xn).
называется двойственной функции f(x1, …, xn).
Пример: (построение функции, двойственной к исходной)
| x | y | z | f(x, y, z) | 
| 
|
Таблица для двойственной функции f*(x, y, z) при упорядоченном наборе значений переменной получается из таблицы для функции f(x, y, z) построением функции отрицания  и переворачиванием столбца значений от функции
и переворачиванием столбца значений от функции  .
.
Таблица функций, двойственным к элементарным:

| 0* | 
| 1* | x | 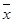
| x* | 
| 
| |||
0* = 1 1* = 0 x* = x 
| x | y | x & y | 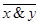
| (x & y)* | x | y | x Ú y | 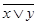
| (x Ú y)* | |
(x & y)* = x Ú y (x Ú y)* = (x & y)
Из определения двойственности вытекает:
f** = (f*)* =  =
=  = f Þ f** = f
= f Þ f** = f
Функция f двойственна к f*
Определение. Если функция f(x1, …, xn) =  , то функция f(x1, …, xn) называется самодвойственной.
, то функция f(x1, …, xn) называется самодвойственной.
Теорема двойственности
Если j(x1, …, xn) = f(f1(x11, …, 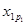 ), …, fm(xm1, …,
), …, fm(xm1, …, 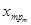 )), где (x1, …, xn) – переменные, входящие в наборы (x11, …,
)), где (x1, …, xn) – переменные, входящие в наборы (x11, …, 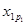 ), …, (xm1, …,
), …, (xm1, …, 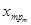 ), то j*(x1, …, xn) = f(f1*(x11, …,
), то j*(x1, …, xn) = f(f1*(x11, …, 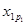 ), …, fm*(xm1, …,
), …, fm*(xm1, …, 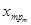 )).
)).
Доказательство: j*(x1, …, xn) º [по определению] º 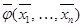 = [по условию] =
= [по условию] =
=  =
=  =
=
=  = [по определению двойственной функции] =
= [по определению двойственной функции] =
= 
Пример: f1(x, y) = x & y, f2(x, y) = x Ú y, f3(x) = 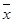 .
.
j = 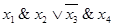 = f2(f1(x1, x2), f1(f3(x3), x4))
= f2(f1(x1, x2), f1(f3(x3), x4))
j* = f2*(f1*(x1, x2), f1*(f3*(x3), x4)) = f1(f2(x1, x2), f2(f3(x3), x4)) = 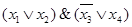 .
.
Принцип двойственности
Если формула A = C[f1, …, fs] реализует формулу f(x1, …, xn), то формула C[f1, …, fs], полученная из формулы f1, …, fs на f1* …, fs* , реализует f*(x1, …, xn). Эту формулу называют двойственной к А и обозначают А*. Для формулы А над множеством P = {0, 1, x, 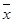 , &, Ú} принцип двойственности записывается так:
, &, Ú} принцип двойственности записывается так:
«Для получения двойственной формулы надо заменить 0 на 1, 1 на 0, & на Ú, Ú на & и сохранить функции x и 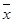 .»
.»
Принцип двойственности позволяет сократить почти в два раза усилия по выводу новых тождеств при рассмотрении свойств элементарных функций.
МАТЕРИАЛ ЭКЗАМЕНА
(Лекция 9)
Разложение булевых функций по переменным
Введем обозначение: 
| x | d | xd | |
| Þ xd = 1 Û x = d | |||
| xx = 1 | |||
Обозначение: 
Теорема (О разложении булевых функций по переменным)
Каждую функцию алгебры логики f(x1, x2, …, xn) для "m Î {1, 2, …, n} можно представить в виде  , где дизъюнкция берется по всевозможным наборам значений d1, …, dm переменных x1, …, xm. Такое представление функции f называется разложением этой функции по m переменным.
, где дизъюнкция берется по всевозможным наборам значений d1, …, dm переменных x1, …, xm. Такое представление функции f называется разложением этой функции по m переменным.
Доказательство: Рассмотрим произвольный набор значений переменных (a1, …, an) и вычислим f(a1, …, an) сначала стандартным образом, а затем так:  = [По ранее доказанному, если ai ¹ di, то
= [По ранее доказанному, если ai ¹ di, то  ] =
] =  = f(a1, …, an).
= f(a1, …, an).
Следствия:
1) m = 1. Тогда f(x1, …, xn) =  =
=  .
.
2) m = n. Тогда f(x1, …, xn) =  , остались лишь те наборы d, при которых f(d1, …, dn) = 1.
, остались лишь те наборы d, при которых f(d1, …, dn) = 1.
f(x1, …, xn) =  , f(d1, …, dn) = 1 , f(d1, …, dn) = 1
|
Такое различие называется Совершенной Дизъюнктивной Нормальной Формулой (СДНФ).
Пример:
| x1 | x2 | x3 | f | f1 | f2 | f3 | f = f1Ú f2 Ú f3

 - СДНФ - СДНФ
| |
Существует еще и Совершенная Конъюнктивная Нормальная Формула (СКНФ):
f(x1, …, xn) =  , f(d1, …, dn) = 1 , f(d1, …, dn) = 1
|
Только для функции «0» мы не можем составить СДНФ.
По аналогии, не существует СКНФ для функции «1».
Полином Жегалкина
Если формула алгебры логики составлена исключительно из функций 0, 1, &, Å, то после несложных преобразований ее можно записать в виде полинома по «Сумме по модулю 2».
Определение. Полиномом Жегалкина от n переменных x1, …, xn называется «Сумма по модулю 2»:  .
.
Пример: ПЖ(x1, x2) = a11x1x2Å a1x1Å a2x2Å ao
Слагаемых в этой сумме столько, сколько подмножеств (j1, …, js) из n чисел, то есть 2n, при этом значения коэффициентов  . Таким образом, число полиномов Жегалкина от n переменных равно
. Таким образом, число полиномов Жегалкина от n переменных равно 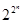 , то есть |ПЖ(n)| =
, то есть |ПЖ(n)| = 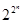 .
.
Теорема Жегалкина
Каждая булева функция может быть выражена с помощью полинома Жегалкина, причем единственным образом.
Пояснение. Различные функции соответствуют различным полиномам Жегалкина, так как число 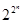 равно числу булевых функций.
равно числу булевых функций.
Замечание. Если у функции есть фиктивные переменные, то они не должны входить в полином Жегалкина.
Способы нахождения Полинома Жегалкина:
1) Через законы Алгебры Логики.
a) Из формулы.
b) Из СДНФ.
2) Метод неопределенных коэффициентов.
Способ 1(а): x Ú y = 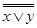 =
=  = (x Å 1) (y Å 1) Å 1 =
= (x Å 1) (y Å 1) Å 1 =  = xy Å x Å y
= xy Å x Å y
Способ 2:
| x | y | x ® y | (x ® y) = a12xy Å a1x Å a2y Å a0 | ||||
| a0 = f(0, 0) = 1 | |||||||
| a0 Å a1 = f(1, 0), 1 Å a1 = 0 Þ a1 = 1 | |||||||
| a2 Å a0 = f(0, 1), 1 Å a2 = 1 Þ a2 = 0 | |||||||
| a12 Å a1 Å a2 Å a0 = f(1, 1), a12 Å 1 Å 0 Å 1 = 1 Þ a12 = 1 |
ПЖ(x ® y) = xy Å x Å 1
Определение. Если полином Жегалкина не содержит конъюнкций, то есть имеет вид a1x1 Å a2x2 Å … Å anxn Å a0, то соответствующая ему функция называется линейной.
Полнота и замкнутость
Определение. Система функций {f1, f2, …, fs}называется полной (функционально полной), если любая булева функция может быть записана в виде формул через функции этой системы ({f1, f2, …, fs} Ì P2).
Пример:
1) P2 – полная.
2) {Ø, &, Ú} – полная Þ Если f(x1, …, xn) º 0, то f(x1, …, xn) = x1 &  .
.
3) {0, 1} – неполная.
Теорема (О полноте системы булевых функций)
Пусть даны 2 системы булевых функций R = {f1, f2, …, fr} (I) и S = {g1, g2, …, gs} (II), причем система I – полная и каждая функция системы I выражается в виде формул системы II. В этом случае система II является полной.
(без доказательства)
Следствие. Полными являются следующие системы: {Ø, Ú}, {Ø, &}, {¤}, {Ø, ®}, {0, 1, &, Å}.
Доказательство:
а) (I) {Ø, &, Ú}. x & y =  =
=  . Аналогично: x Ú y =
. Аналогично: x Ú y =  .
.
б) (I) {Ø, &}. 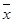 = x / x. Тогда: x & y =
= x / x. Тогда: x & y =  = (x / y) / (x / y).
= (x / y) / (x / y).
Понятие полноты тесно связано с понятием замыкания.
Определение. Пусть М – некоторое подмножество булевых функций. Замыканием М (обозначается [M]) называется множество всех булевых функций, являющихся суперпозицией функций из М.
Пример:
1) М = Р2, [M] = P2.
2) M = {1, x Å y}, f Î M, f = a0 Å a1x1 Å … Å anxn (f – линейная функция).
Свойства замыкания:
1) M Í [M]
2) [[M]] = [M]
3) M1 Í M2 [M1] Í [M2]
4) [M1 È M2] Ê [M1] È [M2]
Определение. Класс (множество) М называется замкнутым (функционально замкнутым), если [M] = M.
(Лекция 10)
Примеры:
1) M = P2, [M] = P2 =M – замкнутое
2) M = L (множество линейных функций), [M] = L = M – замкнутое
3) M = {Ø, &, Ú} Þ [M] =P2 Þ M – замкнутое
4) M = {0, 1}Þ M – неполное, [M] = {0, 1} – замкнутое.
5) M = {1, 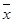 }Þ [M] = {0, 1, x,
}Þ [M] = {0, 1, x, 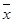 } Þ M – незамкнутое
} Þ M – незамкнутое
6) [M] – замкнутый класс по свойству 2.
|
из
5.00
|
Обсуждение в статье: Принцип двойственности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

