 |
Главная |
Перестановки и подстановки
|
из
5.00
|
47. Найдите  ,
,  ,
,  ,
,  ,
,  ,
,  и порядок каждой из подстановок:
и порядок каждой из подстановок:
а)  ,
,  ;
;
б) 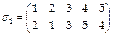 ,
,  ;
;
в)  ,
,  ;
;
г)  ,
,  ;
;
48. Сколькими способами можно обить 6 стульев тканью, если имеются ткани шести цветов и все стулья должны быть разного цвета?
49. Сколькими способами могут расположиться в турнирной таблице 10 команд, если известно, что никакие две команды не набрали поровну очков?
50. Сколько существует способов поставить на книжную полку в беспорядке собрание сочинений, состоящее из 7 томов?
51. Сколько всевозможных кортежей длиной 7 можно составить из слова «кислота»?
52. Сколькими способами можно переставить буквы слова юпитер так, чтобы гласные шли в алфавитном порядке?
2.2. Размещения и сочетания
53. В группе из 26 человек выбирают актив: старосту, физорга, профорга и культорга. Сколькими способами могут избрать актив группы?
54. Сколькими способами можно устроить на работу 8 выпускников факультета программирования на различные должности в 5 вычислительных центрах?
55. Сколько различных спортивных прогнозов могут дать болельщики перед началом первенства по футболу, если в высшей лиге участвуют 15 команд и разыгрываются три медали: золотая, серебряная, бронзовая?
56. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?
57. В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление трех различных видов деталей (по одному виду на каждого).
58. Сколькими способами можно выбрать 5 делегатов из состава конференции на которой присутствуют 15 человек?
59. Группе из пяти сотрудников выделено три путевки. Сколько существует способов распределения путевок, если: а) все путевки различны; б) все путевки одинаковы?
60. Из всех студентов вашей группы на беседу с деканом приглашены пятеро. Сколькими способами это можно сделать?
61. Для проведения итогов олимпиады по компьютерному моделированию избрали жюри в составе председателя, заместителя председателя и трех членов жюри. Сколькими способами можно выбрать жюри из 15 преподавателей кафедры информатики?
62. Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?
63. Лифт, в котором находится 9 пассажиров, может останавливаться на десяти этажах. Пассажиры выходят группами в два, три и четыре человека. Сколькими способами это может произойти?
64. Сколько шестизначных номеров можно составить из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9?
2.3. Перестановки с повторениями
65. Требуется составить расписание отправления поездов на различные дни недели. При этом необходимо, чтобы: 3 дня отправлялись по 2 поезда в день, 2 дня - по 1 поезду в день, 2 дня - по 3 поезда в день. Сколько можно составить различных расписаний?
66. Сколько слов можно получить, переставляя буквы в слове «математика»?
67. Сколькими способами можно разложить 28 различных предметов по четырем различным ящикам, так, чтобы в каждом ящике оказалось по 7 предметов?
68. Сколькими способами можно переставить буквы слова «кофеварка» так, чтобы гласные и согласные буквы чередовались?
69. Сколько различных перестановок образуется из следующих слов: а) зебра; б) баран; в) водород; г) абракадабра?
2.4. Размещения и сочетания с повторениями
70. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта пирожных?
71. Сколькими способами можно разделить 6 различных конфет между тремя детьми?
72. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток?
73. Крокодил имеет 68 зубов. Доказать, что среди 1617 крокодилов может не оказаться двух с одним и тем же набором зубов.
74. Сколько различных десятизначных чисел можно написать, используя цифры 0, 1 и 2?
75. Алфавит X состоит из двух символов. Сколько существует слов алфавита X, длины которых не превосходят 4?
76. Из 15 красных и 7 белых гладиолусов формируют букеты. Сколькими способами можно составить букеты из 4 красных и 3 белых гладиолусов?
2.5.Комбинированные задачи
77. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было не менее 2 женщин. Сколькими способами можно это сделать?
78. Сколькими способами можно положить 28 различных открыток в 4 одинаковых конверта так, чтобы в каждом конверте лежало по 7 открыток.
79. Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?
80. Сколько номеров, состоящих из двух букв, за которыми идут пять цифр, можно составить, использовав 32 буквы и 10 цифр?
81. Во взводе 3 сержанта и 30 солдат. Сколько существует способов выделения одного сержанта и трех солдат для патрулирования?
82. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами их можно посадить в два ряда, чтобы рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
83. Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд, так чтобы при этом два футболиста одной команды не стояли рядом?
84. Два почтальона должны разнести 10 писем по 10 адресатам. Сколькими способами они могут распределить работу?
85. Сколько существует вариантов, чтобы из букв слова «студент» составить всевозможные кортежи длиной 5?
86. Даны n точек на плоскости, никакие три из которых не лежат на одной прямой и никакие 4 - на одной окружности. Через каждые две из этих точек проводится прямая, а через каждые три - окружность. Найти наибольшее число точек пересечения всех проведенных прямых со всеми окружностями.
87. Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколькими различными способами можно посадить четырех человек? А семь человек? Во скольких случаях два данных человека из семи оказываются соседями? Во скольких случаях данный человек (из семи) имеет двух данных соседей?
88. Сколькими способами можно вынуть 4 карты из полной колоды так, чтобы были 3 масти? Так, чтобы были 2 масти?
89. В шахматной олимпиаде участвуют представители n стран по 4 представителя от каждой страны. Сколькими способами можно они могут встать в ряд так, чтобы рядом с каждым был представитель той же страны?
90. Укротитель хочет вывести на арену цирка n львов и k тигров; при этом нельзя, чтобы два тигра шли друг за другом. Сколькими способами он может расположить зверей?
91. Сколько положительных чисел от 20 до 1000 делятся ровно на одно из чисел 7, 11 или 13?
92. Группу из 16 студентов должны разбить на подгруппы для работы в разных компьютерных классах. Сколько существует всех возможных вариантов формирования подгрупп, если в трех компьютерных классах соответственно 5, 4 и 7 работающих ЭВМ?
93. Из цифр 3, 4, 5, 6 составлены четырехзначные числа. Сколько вариантов таких чисел можно найти, если среди найденных четверок нет чисел, заканчивающихся на 36?
94. Сколькими способами можно построить кортежи из букв слова «грамматика»?
95. Сколькими способами можно поставить на полку четырехтомник Пушкина, двухтомник Ахматовой и трехтомник Лермонтова так, чтобы книги каждого автора стояли рядом?
96. На полке стоят 10 книг, 5 из них — Собрание сочинений Л. Н. Толстого. Сколько существует вариантов расстановки книг на полке при условии, что все 5 томов Л. Н.Толстого должны стоять рядом?
97. После окончания колледжа 12 выпускников-программистов решили ежегодно в день встречи с выпускниками посещать кафе и обмениваться впечатлениями. Так как в кафе столики рассчитаны на четырех человек, то друзья решили, что при каждой новой встрече за столиками будет четверка, не повторяющая прошлогодние. За сколько лет каждый из выпускников побеседует с каждым из друзей, сидя за каким-нибудь одним столом?
98. Три девушки и семь юношей распределились на практику в два вычислительных центра. Сколько способов разместить их поровну так, чтобы в каждый вычислительный центр попала хотя бы одна девушка?
99. В состав хоккейной команды входит три нападающих, два защитника и один вратарь. Сколько различных команд из них может составить тренер, если у него занимаются семь нападающих, пять защитников и три вратаря?
100. Когда Гулливер попал в Лилипутию, он обнаружил, что там все вещи ровно в 12 раз короче, чем на родине. Сколько лилипутских спичечных коробков поместится в спичечном коробке Гулливера?
|
из
5.00
|
Обсуждение в статье: Перестановки и подстановки |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

