 |
Главная |
Передаточные функции дискретных систем
|
из
5.00
|
Чтобы найти передаточные функции дискретных систем, как и в случае непрерывных систем, необходимо первоначально определить передаточную функцию разомкнутой системы. Структурная схема на рисунке.
 g x
g x
T T
Передаточная функция
W(Z)=  ,
,
Где X(z), G(z ) - изображение функций времени x(t), g(t). Рассмотрим первоначально простейший случай, когда D(z)=1. В этом случае последовательно соединены идеальный импульсный элемент, экстраполятор и непрерывная часть системы. Экстраполятор и непрерывная часть в совокупности образуют приведенную непрерывную часть, передаточная функция которой определяется выражением
W(s) =Wэ(s) W0(s)
Импульсной переходной функцией или функцией веса приведенной непрерывной части системы является оригинал изображения W(s)
k (t)=L-1[W(s)]
Тогда можно записать
W (Z) =Z{k(t)}=Z{W(s)}.
Таким образом, чтобы найти передаточную функцию W(z) необходимо определить Z-преобразование передаточной функции приведенной непрерывной части.
Пусть в системе используется экстраполятор нулевого порядка. Тогда
Wэ(s)=L{kэ(t)}=  .
.
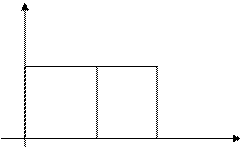 |
kэ
1
0 g T T t
kэ(t)=1(t)-1(t-T)
L[1(t)]= 
L[1(t-T)]=e-TS(  ), т.е. Wэ(S)=
), т.е. Wэ(S)=  ,
,
(если импульсный элемент формирует импульсы с последовательностью g, то Wиэ(S)=  )
)
В этом случае
W(s) =(1-e-Ts) 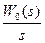 =W1(e-Ts)
=W1(e-Ts) 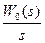 .
.
Для отыскания Z-преобразования функции времени, заданной преобразованием Лапласа в такой форме можно воспользоваться выражением
Z{W(s)}=W1(z)Z{ 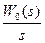 }
}
Поэтому
W(z)=  Z{
Z{ 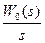 }=
}= 
Z-преобразование Z {  } находится путем разложения рациональной дроби
} находится путем разложения рациональной дроби 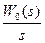 на простые с дальнейшим использованием таблиц Z-преобразований.
на простые с дальнейшим использованием таблиц Z-преобразований.
Пример.
Пусть 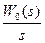 =
= 
Тогда пользуясь таблицей, будем иметь
W(z)=K  Z{
Z{  } =K
} =K  [
[ 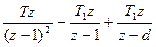 ] ,
] ,
где d=e-(  )
)
Для большинства цифровых систем управления D(z)¹1. В этом случае
W (z)=D(z)Z{W(s)}),
т.к. ЭВМ или цифровое управляющее устройство, осуществляя модуляцию последовательности входных d-функций, не изменяет дискретной природы сигналов.
В любой момент времени nT ЭВМ в соответствии с алгоритмом работы определяет и выдает на выход числовую величину, получаемую в общем случае по значениям входного и выходного сигналов в данный и предшествующие моменты времени.
 |
x1 x2
x2(n)=  aix1(n-i)-
aix1(n-i)-  bix2(n-i) (*)
bix2(n-i) (*)
где i- целое положительное число
Учитывая, что
Z{f[n-i]}=Z-IF(z), где F(z)=Z{f[n]}
Можно записать, что
D(Z)=  и применяя к (*) Z-преобразование
и применяя к (*) Z-преобразование
X2(z)=  aiz-iX1(z)-
aiz-iX1(z)-  biz-iX2(z) или
biz-iX2(z) или
X2(z)=  bIz-i=X1(Z)
bIz-i=X1(Z)  aiz-i,
aiz-i,
где b0=1
Откуда D(Z)= 
Умножив числитель и знаменатель на zl , получим
D (Z)= 
Пример
Пусть ЭВМ реализует функцию корректирующего устройства с алгоритмом
X2[n]=d1x1[n]+d2Ñx1[n]=d1x1[n]+d2{x1[n]-x[n-1]}=
=(d1+d2)x[n]-d2x[n-1]=a0x[n]-a1x[n-1]
X2[Z]= a0X1[z]- a1z-1X1[z];
Тогда
D(Z)= a0-a1z-1= 
Зная D(z) всегда можно определить W(z).
Рассматривая полученные выражения, следует учитывать особый вид дискретной передаточной функции, которую не следует путать с обычной передаточной функцией непрерывного звена, т.к. W(z)¹W(s) при замене в последней символа s на z.
Для систем с единичной обратной связью, если W(z) представляет собой передаточную функцию разомкнутой системы
Ф(z)= 
и передаточную функцию по ошибке
Фe(z)= 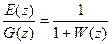
и по возмущению
Фf(z)= 
Знаменатель рассмотренных передаточных функций замкнутой системы называется ее характеристическим полиномом. Обычно изображения входных сигналов и передаточные функции представляют собой дробно-рациональные функции z. Они позволяют использовать различные оценки качества систем регулирования.
|
из
5.00
|
Обсуждение в статье: Передаточные функции дискретных систем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

