 |
Главная |
Отображения на комплексной плоскости
|
из
5.00
|
Лекция 2. Функции комплексного переменного
Основные понятия функций комплексного переменного
Пусть заданы два множества 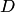 и
и 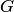 комплексных чисел.
комплексных чисел.
Если каждому значению 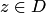 ставится в соответствие число
ставится в соответствие число 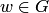 , то говорят, что на множестве
, то говорят, что на множестве 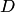 задана функция
задана функция 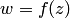 комплексного переменного, т.е.
комплексного переменного, т.е.
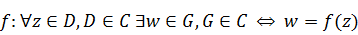
Если записать комплексные числа  и
и 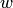 в алгебраической форме:
в алгебраической форме: 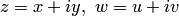 , то замечаем, что действительная
, то замечаем, что действительная 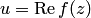 и мнимая
и мнимая 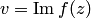 части функции
части функции 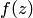 являются функциями действительных переменных
являются функциями действительных переменных 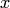 и
и 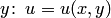 и
и 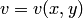 .
.
Задание функции 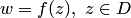 эквивалентно заданию на множестве
эквивалентно заданию на множестве 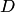 двух функций
двух функций 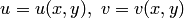 двух действительных переменных.
двух действительных переменных.
Кроме того, если для числа 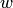 записать модуль
записать модуль 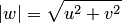 и аргумент
и аргумент 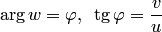 для
для 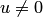 и
и  при
при 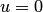
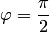 если
если 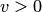 и
и 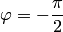 если
если 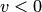 , то получим аналогичное утверждение. Задание функции комплексного переменного
, то получим аналогичное утверждение. Задание функции комплексного переменного 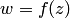 равносильно заданию двух функций двух действительных переменных. Первая из функций определяет модуль функции:
равносильно заданию двух функций двух действительных переменных. Первая из функций определяет модуль функции: 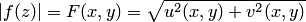 , вторая — аргумент функции:
, вторая — аргумент функции: 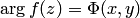 , где
, где 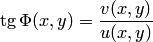 в точках, в которых
в точках, в которых 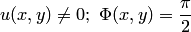 если
если 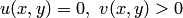 и
и 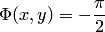 если
если 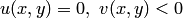 .
.
Пример 1.Найти значение функции 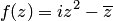 в точках
в точках 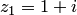 и
и 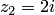 .
.
Решение. 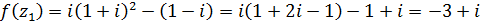 .
.
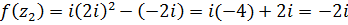 .
.
Пример 2. Найти 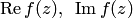 , если а)
, если а) 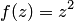 ; б)
; б) 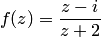 .
.
Решение. а) 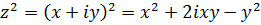 ,
, 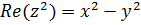 ,
, 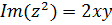 . б)
. б) 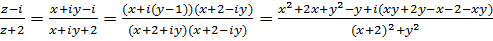 ,
,
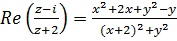 ,
, 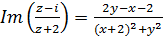 .
.
Отображения на комплексной плоскости
 Задание функции комплексного переменного
Задание функции комплексного переменного 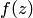 с областью определения
с областью определения 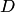 и областью значений
и областью значений 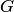 есть отображение множества
есть отображение множества 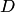 на множество
на множество 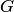 ,
, 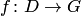 (рис. 3.1).
(рис. 3.1).
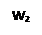
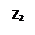




Точка 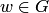 называется образом точки
называется образом точки  при отображении
при отображении 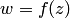 , точка
, точка 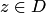 — прообразом.
— прообразом.
По определению предполагается однозначность отображения, т.е. каждому числу 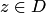 соответствует единственное значение
соответствует единственное значение 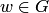 , но при этом может оказаться, что точка
, но при этом может оказаться, что точка 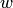 является образом двух или более точек
является образом двух или более точек 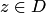 (на рис. 2.1 это точка
(на рис. 2.1 это точка 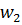 , так как
, так как 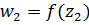 и
и 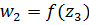 ).
).
Если любое значение 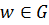 является образом только одной точки
является образом только одной точки 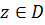 , то отображение называется однолистным в области
, то отображение называется однолистным в области 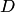 , в противном случае — неоднолистным. Из определения следует, что однолистное отображение является взаимно однозначным отображением.
, в противном случае — неоднолистным. Из определения следует, что однолистное отображение является взаимно однозначным отображением.
Простейшими однолистными (во всей комплексной плоскости) отображениями являются отображения 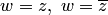 . Первое отображает любую область, в том числе и всю комплексную плоскость, на себя, второе — верхнюю полуплоскость на нижнюю полуплоскость, а нижнюю на верхнюю.
. Первое отображает любую область, в том числе и всю комплексную плоскость, на себя, второе — верхнюю полуплоскость на нижнюю полуплоскость, а нижнюю на верхнюю.
Примером неоднолистного в 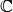 отображения является
отображения является 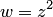 . Действительно, различным точкам, например
. Действительно, различным точкам, например 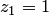 и
и 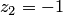 , соответствует одно значение
, соответствует одно значение 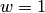 , а точкам
, а точкам 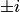 — одно значение
— одно значение 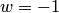 . Неоднолистным отображением является и
. Неоднолистным отображением является и  . Каждой точке
. Каждой точке 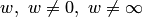 , соответствуют
, соответствуют 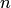 значений
значений  . В силу этого отображение
. В силу этого отображение  если
если 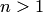 называют n-листным, а отображение
называют n-листным, а отображение 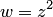 — двулистным.
— двулистным.
Из определения получаем и условие однолистности отображения, отображение является однолистным на множестве 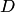 , если для любых точек
, если для любых точек 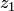 и
и 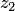 , принадлежащих
, принадлежащих 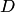 , равенство
, равенство 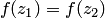 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 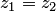 . Иначе: отображение однолистно на множестве
. Иначе: отображение однолистно на множестве  , если множество не содержит ни одной пары чисел
, если множество не содержит ни одной пары чисел 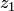 и
и 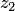 , таких, что
, таких, что 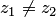 и выполняется условие
и выполняется условие 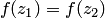 .
.
Пример 3. Найти область однолистности функции 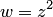 .
.
Решение.Во всей комплексной плоскости отображение не является однолистным. Но можно найти множество, где условие однолистности будет выполнено, то есть множество, которое не содержит двух различных точек 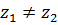 , для которых выполняется равенство
, для которых выполняется равенство 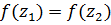 . Рассмотрим разность
. Рассмотрим разность 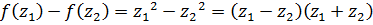 . При
. При 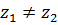 равенство
равенство 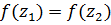 выполняется, если
выполняется, если 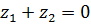 . Таким образом, функция однолистна в области, которая не содержит две точки
. Таким образом, функция однолистна в области, которая не содержит две точки 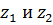 такие, что
такие, что 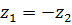 . Эти точки надо расположить на границе области. Так как этому условию удовлетворяют точки симметричные начала координат, то в качестве границы области следует взять любую кривую, проходящую через начало координат. Например, такой областью является полуплоскость
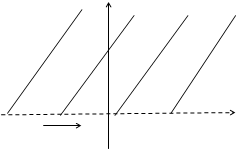
. Эти точки надо расположить на границе области. Так как этому условию удовлетворяют точки симметричные начала координат, то в качестве границы области следует взять любую кривую, проходящую через начало координат. Например, такой областью является полуплоскость 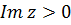 . Причем, она отображается во всю комплексную плоскость с разрезом по действительной полуоси, которая пробегается дважды. На рис. 3.2 направление обхода указано стрелкой. Аналогично полуплоскость
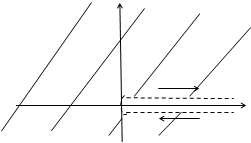
. Причем, она отображается во всю комплексную плоскость с разрезом по действительной полуоси, которая пробегается дважды. На рис. 3.2 направление обхода указано стрелкой. Аналогично полуплоскость  отображается во всю плоскость с разрезом, только меняется направление обхода.
отображается во всю плоскость с разрезом, только меняется направление обхода.
 | |||
 |
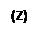

Пример 4. Исследовать на однолистность отображения: а) 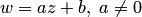 ; б)
; б) 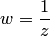 ; в)
; в)  .
.
Решение.а) Отображение однолистно во всей комплексной плоскости, так как для 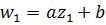 и
и 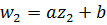 равенство
равенство 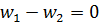 выполняется только тогда, когда
выполняется только тогда, когда 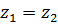 .
.
б) При 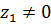 и
и 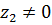 имеем
имеем 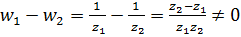 , если
, если 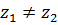 . Отображение однолистно в любой области, не содержащей начало координат.
. Отображение однолистно в любой области, не содержащей начало координат.
в) Во всей плоскости функция не является однолистной, так как, например, для точек 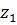 и
и 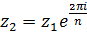 значения функции совпадают, так как
значения функции совпадают, так как 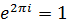 .
.
Однолистным отображение будет в любой области, принадлежащей углу раствора 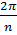 с вершиной в начале координат. Каждый такой угол функция
с вершиной в начале координат. Каждый такой угол функция 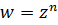 отображает на всю плоскость с разрезом по лучу
отображает на всю плоскость с разрезом по лучу  (рис. 3.3).
(рис. 3.3).
 |
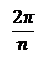
|
из
5.00
|
Обсуждение в статье: Отображения на комплексной плоскости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

