 |
Главная |
Критерий согласи Пирсона
|
из
5.00
|
Проверим, согласуются ли полученные данные с гипотезой  о нормальном распределении
о нормальном распределении  , используя критерий согласия Пирсона, где
, используя критерий согласия Пирсона, где 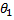 =
= 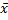 ,
, 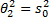 - ранее вычисленные выборочные характеристики.
- ранее вычисленные выборочные характеристики.
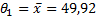 ;
; 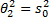 =214,38
=214,38
 .
.
Задаем уровень доверия γ=0, 95 и уровень значимости α=0,05.
В таблице 9 приведено использование критерия Пирсона для  :
:  .
.
Таблица 9.
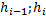
| 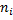
| 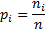
| 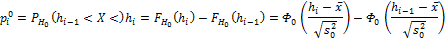
| 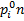
| 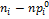
| 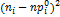
| 
| |
| 7,5-12,5 | 0,0061 | 0,00336 | 3,3197 | 2,6803 | 7,1841 | 2,1641 | ||
| 12,5-17,5 | 0,0091 | 0,00832 | 8,2202 | 0,7798 | 0,6082 | 0,0740 | ||
| 17,5-22,5 | 0,0142 | 0,01719 | 16,9837 | -2,9837 | 8,9026 | 0,5242 | ||
| 22,5-27,5 | 0,0364 | 0,03227 | 31,8828 | 4,1172 | 16,9517 | 0,5317 | ||
| 27,5-32,5 | 0,0466 | 0,05401 | 53,3619 | -7,3619 | 54,1973 | 1,0157 | ||
| 32,5-37,5 | 0,0870 | 0,08064 | 79,6723 | 6,3277 | 40,0395 | 0,5026 | ||
| 37,5-42,5 | 0,1053 | 0,10737 | 106,0816 | -2,0816 | 4,3329 | 0,0408 | ||
| 42,5-47,5 | 0,1285 | 0,12748 | 125,9502 | 1,0498 | 1,1020 | 0,0087 | ||
| 47,5-52,5 | 0,1377 | 0,13891 | 137,2431 | -1,2431 | 1,5452 | 0,0113 | ||
| 52,5-57,5 | 0,1265 | 0,12705 | 125,5254 | -0,5254 | 0,2760 | 0,0022 | ||
| 57,5-62,5 | 0,1073 | 0,10664 | 105,3603 | 0,6397 | 0,4092 | 0,0039 | ||
| 62,5-67,5 | 0,0820 | 0,07982 | 78,8622 | 2,1378 | 4,5704 | 0,0580 | ||
| 67,5-72,5 | 0,0516 | 0,05329 | 52,6505 | -1,6505 | 2,7242 | 0,0517 | ||
| 72,5-77,5 | 0,0324 | 0,03174 | 31,3591 | 0,6409 | 0,4107 | 0,0131 | ||
| 77,5-82,5 | 0,0162 | 0,01717 | 16,9640 | -0,9640 | 0,9292 | 0,0548 | ||
| 82,5-87,5 | 0,0081 | 0,00779 | 7,6965 | 0,3035 | 0,0921 | 0,0120 | ||
| 87,5-92,5 | 0,0051 | 0,00695 | 6,8666 | -1,8666 | 3,4842 | 0,5074 | ||
| S |  = 5,5760 = 5,5760
|
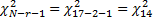 , где r - число параметров выбранной модели; r=2.
, где r - число параметров выбранной модели; r=2.
Статистика критерия Пирсона:
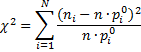
где N – число интервалов;  - гипотетические вероятностные события.
- гипотетические вероятностные события.
Из теоремы Пирсона имеем:


 По таблице для
По таблице для  находим
находим 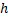 :
:  =0,95 ⇒
=0,95 ⇒ 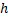 =23,685
=23,685
доверительная область критическая область
 почти достоверных событий, маловероятных событий,
почти достоверных событий, маловероятных событий,
 если гипотеза
если гипотеза 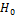 верна, если гипотеза
верна, если гипотеза 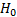 верна
верна
p=γ 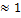
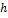 1-γ=α
1-γ=α 
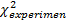 = 5,5760
= 5,5760




 Доверительная область критическая область
Доверительная область критическая область
5,5760 23,685
Так как 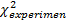 = 5,5760 попало в доверительную область, то никаких противоречий с гипотезой
= 5,5760 попало в доверительную область, то никаких противоречий с гипотезой  не наблюдается; гипотеза
не наблюдается; гипотеза  принимается с уровнем значимости α=1-γ. Другими словами, гипотеза
принимается с уровнем значимости α=1-γ. Другими словами, гипотеза  на γ
на γ  100% согласуется с экспериментальными данными, а возможна ошибка 100% согласуется с экспериментальными данными, а возможна ошибка α
100% согласуется с экспериментальными данными, а возможна ошибка 100% согласуется с экспериментальными данными, а возможна ошибка α  100%.
100%.
Критерии значимости.
1). Принимая определенную статистическую гипотезу о распределении вероятностей с помощью критериев значимости, проверим нулевую гипотезу о неизвестных параметров распределения.
Принимая гипотезу 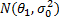 , проверим гипотезу
, проверим гипотезу  :
:  =50;
=50; 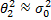 =225.
=225.
 - заранее данное число, дисперсия известна.
- заранее данное число, дисперсия известна.
В ходе проведения эксперимента n=988; 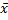 =49,92.
=49,92.
Гипотеза  :
: 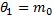 =50 (то есть, проверим, можно ли округлять как в школе).
=50 (то есть, проверим, можно ли округлять как в школе).
Альтернативная гипотеза  :
: 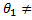 50.
50.
Уровень значимости: α=0,05; уровень доверия γ=0,95.
Статистика критерия значимости:  .
.
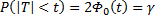 ;
;
 .
.
 Из таблицы для функции Лапласа найдем t: t=1,96.
Из таблицы для функции Лапласа найдем t: t=1,96.
 | |||
 |
критическая обл-ть доверительная обл-ть критическая обл-ть
 γ
γ 
 маловероятные события,
маловероятные события,  почти достоверные
почти достоверные 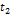 маловероятные события,
маловероятные события,
если гипотеза  события, если гипотеза
события, если гипотеза  если гипотеза
если гипотеза 
верна верна верна
Теперь посчитаем реализацию T для нашего конкретного эксперимента:
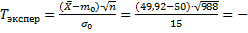 0,1697
0,1697

критическая обл-ть доверительная обл-ть критическая обл-ть


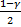 =0,025 γ=0,95
=0,025 γ=0,95  =0,025
=0,025
-1,96 -0,1697 1,96
 0,1697 попадает в доверительную область. Гипотеза
0,1697 попадает в доверительную область. Гипотеза  принимаем с уровнем значимости α=0,05 и уровнем доверия γ=0,95. Значимой разности между
принимаем с уровнем значимости α=0,05 и уровнем доверия γ=0,95. Значимой разности между 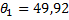 и
и  50 нет.
50 нет.
2). Принимая определенную статистическую гипотезу о распределении вероятностей с помощью критериев, проверим нулевую гипотезу о неизвестных параметрах распределения.
Принимая гипотезу  ,проверим гипотезу
,проверим гипотезу  :
: 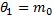 =50;
=50; 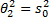 =214,38.
=214,38.
В данном случае дисперсия не задана, т.е. неизвестна, но заменяется на расчетную единицу 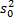 .
.
В ходе проведения эксперимента n=988; 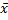 =49,92.
=49,92.
Гипотеза  :
: 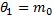 =50 (то есть, проверим, можно ли округлять как в школе).
=50 (то есть, проверим, можно ли округлять как в школе).
Альтернативная гипотеза  :
: 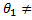 50.
50.
Уровень значимости: α=0,05; уровень доверия γ=0,95.
Статистика критерия значимости:  .
.
Мы будем пользоваться двусторонним распределением Стьюдента с (n-1) степенями свободы (данное распределение табулировано): 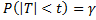 ; n-1=987; α=0,05; γ=0,95.
; n-1=987; α=0,05; γ=0,95.
Из таблицы имеем: 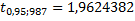 .
.

критическая обл-ть доверительная обл-ть критическая обл-ть
 γ
γ 
 маловероятные события,
маловероятные события,  почти достоверные
почти достоверные 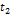 маловероятные события,
маловероятные события,
если гипотеза  события, если гипотеза
события, если гипотеза  если гипотеза
если гипотеза 
верна верна верна
Теперь посчитаем реализацию T для нашего конкретного эксперимента:
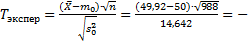 0,1738;
0,1738;

критическая обл-ть доверительная обл-ть критическая обл-ть


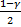 =0,025 γ=0,95
=0,025 γ=0,95 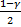 =0,025
=0,025
-1,96 -0,1738 1,96
 0,1738 попадает в доверительную область. Гипотеза
0,1738 попадает в доверительную область. Гипотеза  принимаем с уровнем значимости α=0,05 и уровнем доверия γ=0,95. Значимой разности между
принимаем с уровнем значимости α=0,05 и уровнем доверия γ=0,95. Значимой разности между 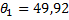 и
и  50 нет.
50 нет.
3). Принимая гипотезу  ,проверим гипотезу
,проверим гипотезу  :
: 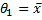 ;
;  .
.
В данном случае уточняем второй параметр нормальной модели, т.е. дисперсию.
В ходе проведения эксперимента n=988; 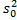 =214,38.
=214,38.
Гипотеза  :
:  =225.
=225.
Альтернативная гипотеза  :
: 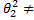 225.
225.
Уровень значимости: α=0,05; уровень доверия γ=0,95.
Статистика критерия значимости: 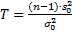 ,
, 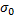 – гипотетическая величина.
– гипотетическая величина.
Доказано, что эта статистика распределена как  с (n-1) степенью свободы,
с (n-1) степенью свободы,  .
.
 ;
;
 |


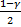 γ
γ 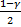
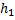

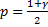
Дело в том, что  табулирована односторонне, т.е.
табулирована односторонне, т.е. 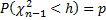 , поэтому придется дважды обратиться к таблице для
, поэтому придется дважды обратиться к таблице для  .
.
Т.к. γ=0,95, то 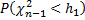 =0,025,
=0,025,  =0,975.
=0,975.
Теперь посчитаем реализацию T для нашего конкретного эксперимента:
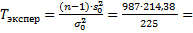 940,416
940,416
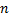 =988 – большое число и по таблице для
=988 – большое число и по таблице для  ни
ни 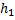 , ни
, ни  не найти.
не найти.
Поэтому воспользуемся ранее полученными результатами:
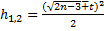 , где
, где  из
из 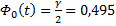 из таблицы для функции Лапласа;
из таблицы для функции Лапласа;  =1,96.
=1,96.
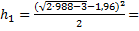 901,361
901,361
 1075,481.
1075,481.
 |

 0,025 0,95 0,025
0,025 0,95 0,025
901,361 940,416 1075,481
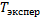 =940,416 попадает в доверительную область. Гипотеза
=940,416 попадает в доверительную область. Гипотеза  принимаем с уровнем значимости α=0,05 и уровнем доверия γ=0,95. Значимой разности между
принимаем с уровнем значимости α=0,05 и уровнем доверия γ=0,95. Значимой разности между  214,38 и
214,38 и  225 нет.
225 нет.
γ-доверительное интервальное оценивание.
Нахождение γ – доверительного интервала. γ=0,95; m=50; σ=15.
1). Гипотеза первая нормальная статистическая модель 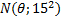 :
:
 ;
;
 – из таблицы Лапласа;
– из таблицы Лапласа;
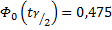 ; таким образом, из таблицы Лапласа
; таким образом, из таблицы Лапласа 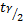 =1,96;
=1,96; 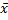 =49,91903.
=49,91903.
Вывод: в среднем случайная величина θ принимает 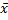 и с вероятностью γ=0,95 колеблется в пределах
и с вероятностью γ=0,95 колеблется в пределах  . В нашем случае колеблется в пределах 49,91903
. В нашем случае колеблется в пределах 49,91903 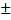 1,96
1,96  .
.
Вывод: θ принимает значение 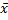 =49,91903 и колеблется в пределах (48,98368974; 50,85436694).
=49,91903 и колеблется в пределах (48,98368974; 50,85436694).
2). Гипотеза вторая нормальная статистическая модель  :
:


 =0,975;
=0,975;
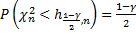 =0,025;
=0,025;
n=988 – большое число и по таблице для 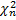
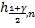 и
и 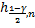 не найти, поэтому воспользуемся ранее полученными результатами:
не найти, поэтому воспользуемся ранее полученными результатами:
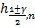 =
= 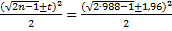 ;
;
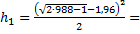 902,31649;
902,31649;
 1076,52511.
1076,52511.
Вывод:  принимает значение
принимает значение 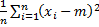 и колеблется в пределах
и колеблется в пределах 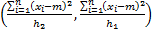 .
.
Найдем теперь эти пределы.
В качестве 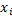 возьмем середины интервалов. Результаты вычислений представлены в виде таблицы:
возьмем середины интервалов. Результаты вычислений представлены в виде таблицы:  =50.
=50.
| Интервалы a=7,5, b=92,5, h=5 | частоты
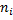
| Середины интервалов 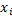
| 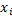 -50 -50
| 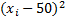
| 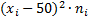
| |
| 7,5-12,5 | -40 | |||||
| 12,5-17,5 | -35 | |||||
| 17,5-22,5 | -30 | |||||
| 22,5-27,5 | -25 | |||||
| 27,5-32,5 | -20 | |||||
| 32,5-37,5 | -15 | |||||
| 37,5-42,5 | -10 | |||||
| 42,5-47,5 | -5 | |||||
| 47,5-52,5 | ||||||
| 52,5-57,5 | ||||||
| 57,5-62,5 | ||||||
| 62,5-67,5 | ||||||
| 67,5-72,5 | ||||||
| 72,5-77,5 | ||||||
| 77,5-82,5 | ||||||
| 82,5-87,5 | ||||||
| 87,5-92,5 | ||||||

| 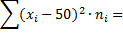
| |||||
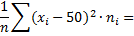
| 214,1700405 | |||||
 902,31649 902,31649
| 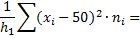
| 234,737926 | ||||
 1076,52511 1076,52511
| 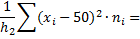
| 196,751475 |
Вывод:  принимает значение 214,1700405 и колеблется в пределах (196,751475; 234,737926).
принимает значение 214,1700405 и колеблется в пределах (196,751475; 234,737926).
3). Общая нормальная статистическая модель  .
.
 (в данной модели) принимает значение
(в данной модели) принимает значение 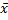 и колеблется в пределах
и колеблется в пределах 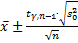 с вероятностью γ=0,95.
с вероятностью γ=0,95.
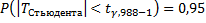 ;
;
При больших значениях n ввиду малой отличаемости из таблицы Стьюдента берут значение для бесконечности; таким образом, 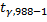 =1,96.
=1,96.
 49,91903;
49,91903; 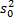 =214,38047.
=214,38047.
Вывод: 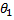 колеблется в пределах (49,00603; 50,83203).
колеблется в пределах (49,00603; 50,83203).
В среднем  принимает значение
принимает значение  и колеблется в пределах
и колеблется в пределах 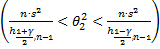 :
:
 =214,16348;
=214,16348;
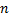 =988 – большое число и по таблице для
=988 – большое число и по таблице для 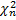
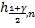 и
и 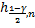 не найти, поэтому воспользуемся ранее полученными результатами:
не найти, поэтому воспользуемся ранее полученными результатами:
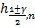 =
= 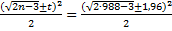 ;
;
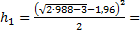 901,36061;
901,36061;
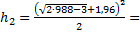 1075,48199.
1075,48199.
Вывод:  колеблется в пределах (196,743154; 234,749023).
колеблется в пределах (196,743154; 234,749023).
Можно вместо  взять
взять 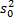 , тогда
, тогда  колеблется в пределах (196,942489; 234,986864).
колеблется в пределах (196,942489; 234,986864).
|
из
5.00
|
Обсуждение в статье: Критерий согласи Пирсона |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

