Второй признак равенства треугольников

Билет № 1

Первый признак равенства треугольников.

Первый признак равенства треугольника по двум сторонам и углу между ними формулируется в виде:

Теорема. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство.

Рассмотрим ΔABC и ΔA₁B₁C₁, у которых AB=A₁B₁, AC=A₁C₁, А= А₁. Докажем, что ΔABC=ΔA₁B₁C₁. Так как A= A₁ то треугольник ABC можно наложить на треугольник А₁В₁С₁ так, что вершина А совместится с вершиной A₁ а стороны АВ и АС наложатся соответственно на лучи А₁В₁ и А₁С₁. Поскольку АВ=A₁B₁, AC=A₁C₁ то сторона АВ совместится со стороной A₁B₁ а сторона АС — со стороной A₁C₁ в частности, совместятся точки В и В₁ С и С₁. Следовательно, совместятся стороны ВС и В₁С₁. Итак, треугольники ABC и A₁B₁C₁ полностью совместятся, значит, они равны. Теорема доказана.

Запись на доске:

Дано: ΔABC, ΔA₁B₁C₁, AB=A₁B₁, AC=A₁C₁, А= А₁.

Доказать: ΔABC=ΔA₁B₁C₁

Доказательство. A= A₁ ═> ΔABC можно наложить на ΔА₁В₁С₁ так, что А→A₁ а АВ и АС наложатся на лучи А₁В₁ и А₁С₁.

АВ=A₁B₁, AC=A₁C₁ ═> АВ → A₁B₁ а АС → A₁C₁ В частности, В → В₁ С → С₁. Следовательно, ВС → В₁С₁. Итак, ΔABC → ΔA₁B₁C₁ полностью, значит, ΔABC=ΔA₁B₁C₁.

Параллелограмм. Определение, свойства, признаки.

Определение. Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

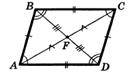Четырехугольник ABCD имеет стороны AB║DC, а сторона BC║AD. Следовательно ABCD –параллелограмм. АС и ВD – диагонали параллелограмма.

Свойства:

1) В параллелограмме противоположные стороны равны и противоположные углы равны (AB=DC, BC=AD, ÐA=ÐC, ÐB=ÐD).

2) Диагонали параллелограмма точкой пересечения делятся пополам (BF=FD, AF=FC).

3) сумма углов, прилежащих к одной стороне равна 180⁰ (ÐA+ÐВ= ÐС+ÐD=ÐВ+ÐC=ÐА+ÐD=180⁰)

Признаки:

1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

2) Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.

3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то он параллелограмм.

Запись на доске:

Свойства:

1) AB=DC, BC=AD, ÐA=ÐC, ÐB=ÐD.

2) BF=FD, AF=FC.

3) ÐA+ÐВ= ÐС+ÐD=ÐВ+ÐC=ÐА+ÐD=180⁰)

Признаки:

1) Если ABСD - четырёхуг., и AB║DC и AB=DC, то – ABСD парал-м.

2) Если ABСD - четырёхуг., и AB=DC, BC=AD, то – ABСD парал-м.

3) Если ABСD - четырёхуг., и BF=FD, AF=FC, то – ABСD парал-м..

Задача.

Билет № 2

Второй признак равенства треугольников.

Второй признак равенства треугольника по стороне и двум прилежащим к ней углам формулируется в виде теоремы.

Теорема: Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника то такие треугольники равны.

Доказательство:РассмотримΔABC и ΔA₁B₁C₁, у которых AB=A₁B₁, А= А₁, ÐB=ÐB_1. Докажем, что ΔABC=ΔA₁B₁C_1. Наложим треугольник ABC на треугольник A₁B₁C₁ так, чтобы вершина A совместилась с вершиной A₁, сторона AB – со стороной A₁B₁, а вершины C и C₁ оказались по одну сторону со стороны A₁B₁. Поскольку ÐA=ÐA₁, ÐB=ÐB₁, то сторона AC наложится на сторону A₁C₁, а сторона BC – на B₁C₁. Вершина C общая точка сторон AC и BC окажется как на стороне A₁C₁ так и на стороне B₁C₁, т.е. совместится с общей точкой этих сторон C₁. Значит стороны AC и A₁C₁, BC и B₁C₁ совместятся, следовательно, и совместятся треугольники ABC и A₁B₁C₁. Отсюда следует, что они равны: ∆ABC=∆A₁B₁C₁

Запись на доске:

Дано: ΔABC, ΔA₁B₁C₁, AB=A₁B₁, А= А₁, ÐB=ÐB_1.

Доказать: ΔABC=ΔA₁B₁C₁

Доказательство:Наложим ΔABC на ΔA₁B₁C₁ так, чтобы A → A₁, AB → A₁B₁, а вершины C и C₁ оказались по одну сторону со стороны A₁B₁.

ÐA=ÐA₁, ÐB=ÐB₁ ═>AC наложится на A₁C₁, а сторона BC – на B₁C₁.

C AC, C BC ═> C A₁C₁, C B₁C₁, ═> С→C₁.

Значит стороны AC → A₁C₁, BC → B₁C₁, ═> ΔABC → ΔA₁B₁C₁.

Значит, ∆ABC=∆A₁B₁C₁