 |
Главная |
Понятие функции, её свойства
|
из
5.00
|
Переменная величина y называется числовой функцией переменной величины x, если каждому возможному числовому значению величины x ставится в соответствие по какому-нибудь правилу или закону единственное числовое значение величины y.
Обозначение:  или
или  , где x — это независимая переменная, или аргумент; y — это зависимая переменная или функция.
, где x — это независимая переменная, или аргумент; y — это зависимая переменная или функция.
Множество задания функции X и множество значений функции Y для числовых функций традиционно называют областью определения функции (ООФ) и областью значений функции (ОЗФ).
Область определения и область значений функции
Областью определения функции (ООФ)  называется множество числовых значений, которые может принимать аргумент
называется множество числовых значений, которые может принимать аргумент  .
.
Областью значений функции (ОЗФ)  называется множество числовых значений, которые принимает функция, если ее аргумент х принадлежит области определения функции.
называется множество числовых значений, которые принимает функция, если ее аргумент х принадлежит области определения функции.
ООФ – это основная характеристика любой функции, с учетом которой исследуются все остальные характеристики;
находится чаще всего как подмножество X множества действительных чисел, на котором выполнимы все операции, определяющие значение функции у по значению ее аргумента х; в этом случае ООФ называют естественной областью определения функции;
может находиться по смыслу функции  и в этом случае будет более узкой, чем естественная ООФ;
и в этом случае будет более узкой, чем естественная ООФ;
приняты и другие обозначения ООФ, например,  .
.
Пример 1. Найти область определения функции  .
.
ООФ: 
ООФ записана из ограничения по делению: на ноль делить нельзя.
Пример 2. Найти область определения функции 
ООФ:  .
.
ООФ определена операцией извлечения корня квадратного, которая имеет смысл только для неотрицательных чисел.
Нули функции и промежутки знакопостоянства.
Нулем функции  называется такое значение
называется такое значение  ее аргумента, при котором значение функции равно нулю:
ее аргумента, при котором значение функции равно нулю:  .
.
Промежутком знакопостоянства функции y=f(x) называется промежуток значений ее аргумента  , во всех точках которого функция принимает значения одного знака.
, во всех точках которого функция принимает значения одного знака.
Пример 3. Найти промежутки знакопостоянства функции  .
.
Решение. ООФ:  ;
;

Данная функция имеет два нуля, которые разбивают ее ООФ на промежутки знакопостоянства функции.
Знак функции на каждом из обозначенных промежутков можно определить по точке-представительнице промежутка, вычислив значение функции в ней:

Четность, нечетность функций
Функция  называется четной функцией, если выполняются два условия:
называется четной функцией, если выполняются два условия:
1) её ООФ симметрична относительно нуля;
2)  .
.
Функция  называется нечетной функцией, если выполнены два условия:
называется нечетной функцией, если выполнены два условия:
1) её ООФ симметрична относительно нуля;
2)  .
.
Пример 4. Исследовать функцию  на чётность/нечётность.
на чётность/нечётность.
Решение. ООФ:  => ООФ симметрична относительно нуля.
=> ООФ симметрична относительно нуля.
Вычисляем у(-х), используя четность основных элементарных функций:

Равенство у(-х)=у(х) выполняется для всех  , поэтому данная функция является четной.
, поэтому данная функция является четной.
Пример 5. Исследовать функцию  на чётность/нечётность.
на чётность/нечётность.
Решение.  . ООФ является симметричной относительно нуля.Вычисляем у(-х):
. ООФ является симметричной относительно нуля.Вычисляем у(-х):
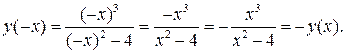
Равенство у(-х)=у(х) выполняется для всех  . Поэтому данная функция является нечетной.
. Поэтому данная функция является нечетной.
Пример 6. Исследовать функцию  на чётность/нечётность.
на чётность/нечётность.
Решение.  . ООФ не является симметричной относительно нуля. Поэтому свойством четности или нечетности эта функция обладать не может. Следовательно, она относится к функциям общего вида, которые не являются ни четными, ни нечетными.
. ООФ не является симметричной относительно нуля. Поэтому свойством четности или нечетности эта функция обладать не может. Следовательно, она относится к функциям общего вида, которые не являются ни четными, ни нечетными.
|
из
5.00
|
Обсуждение в статье: Понятие функции, её свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

