 |
Главная |
Оценка абсолютной погрешности метода средних прямоугольников
|
из
5.00
|
Суть метода прямоугольников.
Пусть функция y = f(x) непрерывна на отрезке [a; b]. Нам требуется вычислить определенный интеграл  .
.
Обратимся к понятию определенного интеграла. Разобьем отрезок [a;b] на n частей  точками
точками  . Внутри каждого отрезка
. Внутри каждого отрезка  выберем точку
выберем точку  . Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения
. Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения  , то любая из интегральных сумм является приближенным значением интеграла
, то любая из интегральных сумм является приближенным значением интеграла 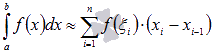 .
.
Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму (далее мы покажем, какую именно интегральную сумму берут в методе прямоугольников).
Метод средних прямоугольников.
Формула метода средних прямоугольников.
Если отрезок интегрирования [a;b] разбить на РАВНЫЕ части длины h точками 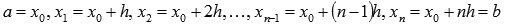 (то есть
(то есть 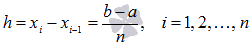 ) и в качестве точек
) и в качестве точек  выбрать СЕРЕДИНЫ элементарных отрезков
выбрать СЕРЕДИНЫ элементарных отрезков  (то есть
(то есть 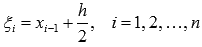 ), то приближенное равенство
), то приближенное равенство 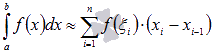 можно записать в виде
можно записать в виде  . Это и есть формула метода прямоугольников. Ее еще называют формулой средних прямоугольников из-за способа выбора точек
. Это и есть формула метода прямоугольников. Ее еще называют формулой средних прямоугольников из-за способа выбора точек  .
.
 называют шагом разбиения отрезка [a;b].
называют шагом разбиения отрезка [a;b].
Приведем графическую иллюстрацию метода средних прямоугольников.

Из чертежа видно, что подынтегральная функция y=f(x) приближается кусочной ступенчатой функцией  на отрезке интегрирования.
на отрезке интегрирования.
С геометрической точки зрения для неотрицательной функции y=f(x) на отрезке[a;b] точное значение определенного интеграла представляет собой площадь криволинейной трапеции, а приближенное значение по методу прямоугольников – площадь ступенчатой фигуры.

Оценка абсолютной погрешности метода средних прямоугольников.
Перейдем к оценке абсолютной погрешности метода прямоугольников. Сначала оценим погрешность на элементарном интервале. Погрешность метода прямоугольников в целом будет равна сумме абсолютных погрешностей на каждом элементарном интервале.
На каждом отрезке  имеем приближенное равенство
имеем приближенное равенство  . Абсолютную погрешность метода прямоугольников
. Абсолютную погрешность метода прямоугольников  на i-ом отрезке вычисляем как разность между точным и приближенным значением определенного интеграла:
на i-ом отрезке вычисляем как разность между точным и приближенным значением определенного интеграла:  . Так как
. Так как  есть некоторое число и
есть некоторое число и  , то выражение
, то выражение  в силу четвертого свойства определенного интеграла можно записать как
в силу четвертого свойства определенного интеграла можно записать как  . Тогда абсолютная погрешность формулы прямоугольников на i-ом элементарном отрезке будет иметь следующий вид
. Тогда абсолютная погрешность формулы прямоугольников на i-ом элементарном отрезке будет иметь следующий вид
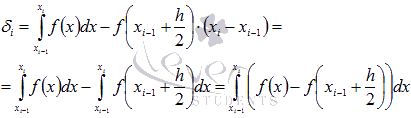
Если считать, что функция y = f(x) имеет в точке 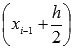 и некоторой ее окрестности производные до второго порядка включительно, то функцию y = f(x)можно разложить в ряд Тейлора по степеням
и некоторой ее окрестности производные до второго порядка включительно, то функцию y = f(x)можно разложить в ряд Тейлора по степеням  с остаточным членом в форме Лагранжа:
с остаточным членом в форме Лагранжа:
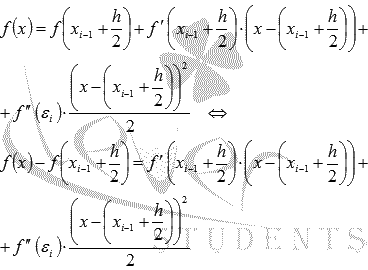
По свойствам определенного интеграла равенства можно интегрировать почленно:

где  .
.
Таким образом, 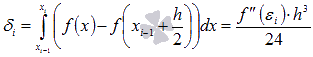 и
и  .
.
Абсолютная погрешность формулы прямоугольников на отрезке [a; b] равна сумме погрешностей на каждом элементарном интервале, поэтому
 и
и 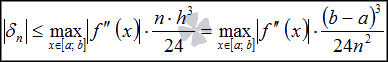 .
.
Полученное неравенство представляет собой оценку абсолютной погрешности метода прямоугольников.
К началу страницы
|
из
5.00
|
Обсуждение в статье: Оценка абсолютной погрешности метода средних прямоугольников |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

