Сначала просто задача

Листок 6. Метод математической индукции.

Задача 6.0. Из квадрата 16ґ16 произвольно вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на "уголки" из трех клеток.

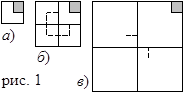
Решение. Попытаемся сначала решить более простую аналогичную задачу. Во-первых, уменьшим размеры квадрата (например, до 4ґ4 или 2ґ2), а, во-вторых, временно зафиксируем вырезанную клетку в углу квадрата. Ну, с квадратом 2ґ2, вообще все просто, – какую бы клетку мы не вырезали, оставшиеся три клетки образуют требуемый "уголок" (рис. 1а). А что же делать в квадрате 4ґ4? Разрежем его на четыре квадратика 2ґ2. С тем, у которого имеется вырезанная клетка, все ясно. Если далее попытаться разрезать оставшийся "большой уголок" на маленькие, то оказывается, что это можно сделать единственным способом (вспомните известную задачу на разрезание из вступительных экзаменов во "Вторую школу"), причем один из получившихся уголков будет принадлежать всем трем квадратикам 2ґ2 (рис. 1б), вырезая из каждого именно угловую клетку. Попробуем теперь разрезать на уголки квадрат 8ґ8 с вырезанным уголком. Делим его на четыре квадрата 4ґ4: с одним – все ясно, у остальных вырежем "уголок" из трех клеток, примыкающий к центру большого квадрата. Каждый из квадратов при этом потеряет по одной клетке, причем опять же именно по угловой (рис. 1в), а значит, оставшиеся части (как мы уже знаем) можно разрезать на "уголки" из трех клеток.

Наверное, все уже поняли, что произойдет дальше. По аналогичному сценарию мы можем разрезать на требуемые "уголки" и квадрат 16ґ16, и квадрат 32ґ32, и т.д. Однако мы забыли, что задача звучала несколько иначе, нежели та, которую мы пока решили, а именно: вырезается из квадрата 16ґ16 не угловая клетка, а произвольная! Что же делать?

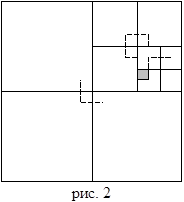
Довести полученное нами решение до искомого не так уж и трудно. Квадрат 16ґ16 делим на четыре квадрата 8ґ8, один из которых (тот, где вырезанная клетка) делим на четыре квадрата 4ґ4, один из них опять же делим на четыре квадрата 2ґ2 и начинаем вырезать "уголки". Сначала в том квадратике, где имеется вырезанная клетка, затем "уголки" от трех оставшихся квадратиков 2ґ2, 4ґ4 и 8ґ8 (рис. 2). Далее каждый из оставшихся квадратов с вырезанной угловой клеткой мы умеем разрезать на "уголки" из трех клеток. 

Обсудим решение. Проследим за логикой наших рассуждений. Сначала мы существенно упростили искомую задачу (уменьшили размеры и передвинули, как захотели вырезанную клетку), затем, получив решение самой простой задачи, заметили, что при решении следующей задачи мы можем воспользоваться уже полученным результатом. Далее, как снежный ком – при решении третьей задачи пользуемся результатами второй и так можно продолжать до бесконечности. Ясно, что, идя так по цепочке, мы дойдем до каждого из ее утверждений, значит все они верны. Таким образом, мы доказали даже более сильный факт, чем требовалось: любой квадрат 2ⁿґ2ⁿбез одной клетки можно разрезать на "уголки" из трех клеток.

Описанный процесс очень напоминает всем знакомую детскую игру – выстраиваешь, друг за другом костяшки домино, а затем толкаешь первую. Она повалит вторую, та – третью и так до тех пор, пока не упадут все (рис. 3). Только в наших рассуждениях вместо падающих доминошек – последовательные доказательства утверждений. Доказали одно, оно влечет за собой доказательство следующего, следующее – дальше и т.д.

Задача 6.1. Имеется 2187 одинаковых на вид монет. Одна из них фальшивая – легче, чем настоящая. Все настоящие монеты весят одинаково. Докажите, что с помощью чашечных весов без гирь можно определить фальшивую монету не более, чем за семь взвешиваний.

Основные определения.

Прежде, чем вводить какие-либо определения заметим, что в предыдущих рассуждениях (задача 6.0) все доказываемые утверждения были очень похожи, отличались только степенью двойки в размерах квадрата. Поэтому естественно занумеровать все эти утверждения. Первое (А₁): квадрат 2¹ґ2¹ без одной клетки можно разбить на "уголки". Второе (А₂): квадрат 2²ґ2²без одной клетки можно разбить на "уголки". Третье (А₃): квадрат 2³ґ2³без одной клетки можно разбить на "уголки"...

Упражнение 1. Сформулируйте пятое, семнадцатое и 2001-е утверждения в этой цепочке.

Упражнение 2. Сформулируйте n-е, (n+1)-е и k-е утверждения в этой цепочке.

Таким образом, можно представить, что все наши утверждения выстроились в очередь (за доказательством!) друг за другом как "доминошки", а мы приготовились их "толкать". Понятно, надо убедиться, что падая, каждая задет и увлечет за собой следующую.

Основная схема. Изложенный выше метод рассуждений требует установления истинности двух фактов:

Факт 1. Первое утверждение верно. (мы можем толкнуть первую доминошку) Факт 2. Если интересующее нас утверждение верно на каком-то шаге, то верно и следующее за ним утверждение. (толкнув одну, уроним и следующую)

Первый факт называется базой (базисом) индукции, второй – индукционным переходом или шагом индукции. Индукционный переход включает в себя посылку (предположение) индукции (утверждение верно при n=k) и заключение (утверждение верно при n=k+1). Другими словами, шаг индукции состоит в переходе от посылки к заключению, т.е. в выводе, что заключение верно, если верна посылка. (если упадет k-я доминошка, то упадет и (k+1)-я

Итак, пусть имеется последовательность утверждений: А₁, А₂, ..., А_n, ... . Для того, чтобы доказать справедливость всех утверждений этой последовательности, можно поступить следующим образом:

1) Доказать истинность утверждения А₁;

2) Доказать, что при любом натуральном n из справедливости утверждения А_n следует справедливость утверждения А_n+1 .

Логический прием, позволяющий заключить, что рассматриваемое утверждение верно для всех натуральных чисел, коль скоро справедливы и базис, и переход называется методом математической индукции (ММИ).

Утверждения A₁, A₂, A₃, … называют частными формулировками, а утверждение "для всякого n имеет место A_n" – универсальной формулировкой. Если мы доказали и базу, и переход, то истинность универсальной формулировки основана на следующем стандартном рассуждении:

Утверждение A1 истинно, т.к. мы доказали базу индукции. Последовательно применяя индукционный переход при k=1, 2, 3, … , получаем истинность утверждений A2, A3, A4, … . Этим способом мы можем последовательно дойти до любого значения n и убедиться, что это An истинно. Следовательно, для всякого n утверждение An справедливо.

Таким образом, метод математической индукции заключается, по существу, в разрешении не пользоваться стандартным рассуждением в каждой конкретной ситуации, т.е. он позволяет сделать заключение об истинности универсальной формулировки сразу, как только установлена истинность базиса индукции и индукционного перехода.

Задача 6.2. Докажите, что при любом натуральном n справедливо равенство: 1 + 2 + 3 + ... + n = .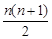

Решение. У нас имеется последовательность утверждений:

А₁: 1 = 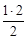; А₂: 1 + 2 = 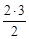; А₃: 1 + 2 + 3 = ; ...

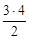1) База индукции: очевидно, что утверждение А₁ верно.

2) Индукционный переход: пусть верно какое-то утверждение А_k, т.е. верно равенство 1 + 2 + 3 +...+ k = 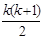(предположение, что А_k верно называется индукционным предположением). Докажем, что тогда верно утверждение А_k+1:

1 + 2 + 3 +...+ k + (k + 1) = 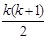+ (k + 1) = + =

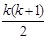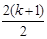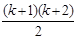
Но это как раз и есть утверждение А_k+1. В силу принципа математической индукции верны все утверждения А₁, А₂, ... , т.е. наша формула верна при любом натуральном n. š

Задача 6.3. Докажите тождество: 1 + 3 + 5 + ... + (2n – 1) = n² для любого натурального n.

Задача 6.4.Докажите тождество: 1²+ 2²+ 3²... + n² = 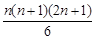для любого натурального n.

Задача 6.5Докажите тождество: 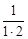+ + 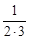+ 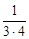... + 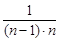= 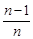для любого натурального n.

Задача 6.6Докажите тождество: (n + 1)(n + 2)...( n + n) = 2ⁿ×1×3×5×...×(2n – 1) для любого натурального n.

Задача 6.7 Докажите тождество: 1×1! + 2×2! + 3×3! + ... + n×n! = (n + 1)! – 1 для любого натурального n.

Замечание 1. Обращаем ваше внимание, что при выполнении индукционного перехода важно показать, что все проводимые рассуждения справедливы для любогоk.

Замечание 2. Вместо утверждения А₁ в качестве базы индукции мы могли взять, например, утверждение А₅. Тогда, выполнив индукционный переход, мы бы доказали, что исходное утверждение верно для всех натуральных n, начиная с 5.[1]

Задача 6.8. Докажите, что сумма углов выпуклого n-угольника равна 180°×(n–2).

Решение. Утверждение задачи имеет смысл при всех натуральных n ³ 3, поэтому и базой индукции будет соответственно n =3.

1) База индукции: утверждение А₃ верно по теореме о сумме углов треугольника.

2) Индукционный переход: выведем заключение о том, что "сумма углов выпуклого (k+1)-угольника равна 180°×((k+1)–2)=180°×(k–1)" из предпосылки "сумма углов выпуклого k-угольника равна 180°×(k–2)". Для этого в (k+1)-угольнике возьмем две вершины по разные стороны от какой-либо одной вершины, и соединим их диагональю (это всегда возможно ввиду выпуклости многоугольника[2]), которая разобьет исходный многоугольник на две части: на треугольник и выпуклый k-угольник. Сумму углов исходного многоугольника можно получить, сложив сумму углов треугольника (180°) и сумму углов k-угольника (180°(k–2) – индукционное предположение!). Складывая эти суммы, получаем 180°(k–1), что и требовалось доказать.š

Задача 6.9.Найдите ошибку в следующем доказательстве: “Докажем, что все натуральные числа равны. База индукции – любое одно число равно самому себе – верно. Пусть доказано для k чисел. Т.е. доказано, что любые k чисел равны между собой. Рассмотрим k+1 число. Если из этого множества выбросить одно из чисел, то их останется ровно k. По индукционному предположению они все равны. Заменим одно из оставшихся чисел на выброшенное ранее. Тогда снова имеем ровно k равных между собой чисел. Следовательно, все k+1 чисел равны между собой. Тем самым утверждение доказано.”

Задача 6.10.Докажите с помощью метода математической индукции следующее утверждение: "В любом n-угольнике количество диагоналей равно ."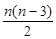

Задачи на делимость.

Техника составления и обоснования индукционных переходов при решении задач на делимость похожа на соответствующую технику для тождеств: для доказательства обычно выясняется КАК изменяется выражение при переходе от k к k +1 и проверяется делимость этого "изменения" на нужное число.

Задача 6.11.Докажите, что n³+(n+1)³+(n+2)³ делится на 9 при любом натуральном n.

Решение. База (n=1): 1³+2³+3³=36 – делится на 9. Переход: пусть при n=k утверждение задачи истинно (т.е. k³+(k+1)³+(k+2)³ M 9 при некотором k). Докажем тогда, что при n=k+1 утверждение также справедливо (т.е. (k+1)³+(k+2)³+(k+3)³ M 9). В самом деле,

,

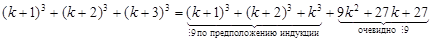а сумма двух чисел, кратных 9, также кратна 9, что и требовалось доказать.š

Задача 6.12.Докажите, что при любом натуральном n 15ⁿ+ 6 кратно 7.

Задача 6.13. Докажите, что при любом натуральном n 7ⁿ+ 3n – 1 кратно 9.

Задача 6.14. Докажите, что при любом натуральном n 2³ⁿ+ 1 кратно 3ⁿ⁺¹.

Задача 6.15.Докажите, что при любом натуральном n 5×2^3n–2+ 3^3n–1 кратно 19.

Задача 6.16.Докажите, что число 111…11 (243 единицы) делится на 243.

Решение.[3] Будем доказывать более общее утверждение, а именно, что число, записываемое 3ⁿединицами, делится на 3ⁿ. База: 111 делится на 3. Переход: пусть доказано, что число, записанное k единицами делится на 3^k. Разделим число, записанное 3^k+1 единицами на число, записанное 3^k единицами. Получим число 100..010..01 (две последовательности нулей по 3^k – 1 штук). Очевидно, что полученное число делится на 3. Следовательно, исходное число делится на 3^k+1 и тем самым индукционный переход, а, значит, и все утверждение доказаны. В частности оно доказано для n=5, поэтому доказано требуемое утверждение, т.к. 243=3⁵.š

Задача 6.17*. Докажите, что существует 100-значное число, делящееся на 2¹⁰⁰, в десятичной записи которого участвуют только цифры 1 и 2.

Неравенства.

Приемы доказательств неравенств более разнообразны, однако, наиболее часто используется следующий факт "сложения неравенств": если а > b и с > d, то a + c > b + d. Здесь в роли неравенства а > b выступает неравенство для k, а с и d – "довески" к левой и правой частям соответственно при переходе от k к k +1.

Задача 6.18.Докажите, что модуль суммы любого числа слагаемых не превосходит суммы модулей этих слагаемых.

Задача 6.19.Докажите, что при любом натуральном n справедливо неравенство 2ⁿ> n.

Задача 6.20.При каких натуральных n выполнено: а) 2ⁿ> 2n + 1; б) 2ⁿ> n² ?

Задача 6.21.Докажите неравенство Бернулли: (1 + х)ⁿ³ 1 + nx при х ³ –1, n Î N.

 

[1] Заметим, что тогда справедливость утверждений 1, 2, 3, 4 мы не доказали и ничего про них не знаем. Такая индукция имеет смысл, когда для меньший значений n утверждение не определено. Например, в задачах про многоугольники число сторон не может быть меньше 3, поэтому нет смысла рассматривать утверждения для "двуугольников" или "одноугольников".

[2] Существует несколько определений выпуклого многоугольника. В данном случае можно использовать любое из двух: Первое – "многоугольник называется выпуклым, если для любых двух его точек А и В отрезок АВ целиком принадлежит этого многоугольнику."(аналогичным образом можно дать определение любой выпуклой фигуры)

Второе – "многоугольник называется выпуклым, если любая диагональ принадлежит ему целиком".

[3] Заметим, что при решении аналогичных задач возникают типичные ошибки: признака делимости на 27, аналогичного признакам делимости на 3 и на 9 – нет; если число делится на 3 и на 9, то совсем не обязательно, что оно делится на 27.