Классификация входных потоков

По характеру входной поток требований разделяется на детерминированный поток требований и стохастический (рис.2).

Детерминированный входной поток может быть двух видов. В первом случае требования поступают через равные промежутки времени. Другим видом детерминированного потока является поток, в котором требования поступают по известной программе - расписанию, когда моменты поступления новых требований известны заранее.

 

Рис.2. Классификация входного потока

 

Если промежутки времени между поступлениями требований случайны, то это будет стохастический процесс.

Стохастический поток требований подразделяется на три вида: поток с произвольными стохастическими свойствами, рекуррентный поток и совершенно случайный или пуассоновский поток требований.

Произвольный поток требований характеризуется тем, что на него не накладывается никаких ограничений на стохастическую независимость интервалов между поступлениями требований, а также на характер вероятностных законов, описывающих интервалы между требованиями.

Входной поток называется рекуррентным, если он характеризуется следующими свойствами:

• продолжительность интервалов между поступлениями требований стохастически независимы;
• продолжительность интервалов описывается одной и той же плотностью распределения.

Входной поток называется совершенно случайным или простейшим, если для него характерно:

• продолжительность интервалов между поступлениями требований статистически независимы;
• продолжительность интервалов описывается одной и той же плотностью распределения;
• вероятность поступления требований на достаточно малом интервале Δt зависит только лишь от величины Δt (это свойство называется стационарностью или однородностью прихода);
• вероятность поступления требований на интервале Δt не зависит от предыстории процесса;
• характер потока требований таков, что в любой момент времени может поступить только одно требование.

Таким образом, простейший поток требований или совершенно случайный поток - это поток, определяющейся свойствами стационарности, ординарности и отсутствием последствия одновременно.

Предположения о совершенно случайном входном потоке требований эквивалентно тому, что плотность распределения интервалов времени между последовательными поступлениями требований описывается экспоненциальным законом:

(1.1)

где λ - интенсивность поступления заявок в систему.

Если интервалы распределены по экспоненциальному закону, то процесс пуассоновский. Такие процессы называются М-процессами (Марковскими).

Кроме закона Пуассона часто применяется закон распределения Эрланга.

(1.2)

СМО с отказами

Одноканальная СМО содержит один канал (n = 1), и на ее вход поступает пуассоновский поток заявок П_вх интенсивность (среднее число событий в единицу времени) которого inП_вх=λ. Так как интенсивность входящего потока может изменяться во времени, то вместо λ записывают λ (t). Тогда время обслуживания каналом одной заявки Т_об распределено по показательному закону и записывается в виде: , где λ - интенсивность отказов.

Состояние СМО характеризуется простаиванием или занятостью ее канала, т.е. двумя состояниями: S₀ - канал свободен и простаивает, S₁ - канал занят. Переход системы из состояния S₀ в состояние S₁ осуществляется под воздействием входящего потока заявок П_вх, а из состояния S₁ в состояние S₀ систему переводит поток обслуживании П_об: если в данный момент времени система находится в некотором состоянии, то с наступлением первого после данного момента времени СМО переходит в другое состояние. Плотности вероятностей перехода из состояния S₀ в S₁ и обратно равны соответственно λ и µ. Граф состояний подобной СМО с двумя возможными состояниями приведен на рис.3.

 

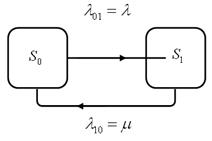
Рис.3. Граф состояний одноканальной СМО с отказами.

 

Для многоканальной СМО с отказами (n > 1) при тех же условиях состояния системы обозначим по числу занятых каналов (по числу заявок, находящихся в системе под обслуживанием, так как каждый канал в СМО либо свободен, либо обслуживает только одну заявку).

Таким образом, подобная СМО может находиться в одном из следующих (n+1) состояний: s₀ - все n каналов свободны; s₁ - занят только один из каналов, остальные (n-1) каналов свободны; s_i - заняты i - каналов, (n-i) каналов свободны; s_n - заняты все n каналов. Граф состояний такой СМО приведен на рис.4.

 

Рис.4. Граф состояний многоканальной СМО с отказами.

При этом имеет место а

Пользуясь общим правилом составления дифференциальных уравнений Колмогорова, можно для приведенных на рис.2 и рис.3 графов состояний составить системы дифференциальных уравнений:

например, для одноканальной СМО (рис.2) имеем:

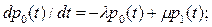
для многоканальной СМО (рис.3) соответственно имеем:

Решив первую систему уравнений, можно найти значения p₀ (t) и p₁ (t) для одноканальной СМО и построить графики при трех случаях:

1) λ >µ;

2) λ=µ;

3) λ<µ

СМО с ожиданием

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью λ. Интенсивность потока обслуживания равна µ (т.е. в среднем непрерывно занятый канал будет выдавать µ обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), т.е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость. Граф состояний СМО в этом случае имеет вид, показанный на рис.6.

 

Рис.6. Граф состояний одноканальной СМО с ожиданием

 

Состояния СМО имеют следующую интерпретацию:

S₀ - канал свободен;

S₁ - канал занят (очереди нет);

S₂ - канал занят (одна заявка стоит в очереди);

S_n - канал занят (n-1 заявок стоит в очереди);

S_N - канал занят (N-1 заявок стоит в очереди).

Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:

(1.11)

где ρ=λ/µ; n - номер состояния.

Решение приведенной выше системы уравнений (1.10) для нашей модели СМО имеет вид:

(1.12)

(1.13)

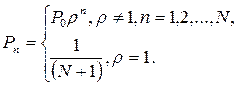
Следует отметить, что выполнение условия стационарности для данной СМО необязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать N-1), а не соотношением между интенсивностями входного потока, т.е. не отношением λ/µ=ρ. Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной (N-1): вероятность отказа в обслуживании заявки:

(1.14)

относительная пропускная способность системы:

(1.15)

абсолютная пропускная способность:

(1.16)

среднее число находящихся в системе заявок:

(1.17)

среднее время пребывания заявки в системе:

(1.18)

средняя продолжительность пребывания клиента (заявки) в очереди:

(1.19)

среднее число заявок (клиентов) в очереди (длина очереди):

. (1.20) [2, 89 - 92].

Теперь рассмотрим более подробно СМО, имеющую n-каналов с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживаний - интенсивность µ. Необходимо найти предельные вероятности состояний СМО и показатели ей эффективности.

Система может находиться в одном состоянии S₀, S₁, S₂,…,S_k,…,S_n,…, нумеруемых по числу заявок, находящихся в СМО: S0 - в системе нет заявок (все каналы свободны); S₁ - занят один канал, остальные свободны; S₂ - заняты два канала, остальные свободны; …, S_k - занято k каналов, остальные свободны; …, S_n - заняты все n каналов (очереди нет); S_{n+1 -} заняты все n каналов, в очереди одна заявка; …, S_{n+r -} заняты все n каналов, r заявок стоит в очереди, ….

Граф состояний показан на рисунке 7.

 

Рис.7. Граф состояний многоканальной СМО с ожиданием

Обратим внимание, что по мере увеличения в СМО от 0 до n увеличивается число каналов обслуживания. При числе заявок в СМО, большем, чем n, интенсивность потока обслуживания сохраняется равной nµ.

Формулы для предельных состояний СМО с ожиданием выглядят следующим образом:

(1.27)

(1.28)

(1.29)

Вероятность того, что заявка окажется в очереди равна:

(1.30)

Для n-канальной СМО с ожиданием, используя прежние формулы, можно найти:

среднее число занятых каналов:

(1.31)

среднее число заявок в очереди:

(1.32)

среднее число заявок в системе:

(1.31) [4, 349 - 360].