Оценка параметров уравнения множественной регрессии. Частные уравнения регрессии

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов. В результате его применения строится система нормальных уравнений, решение которой позволяет определить параметры уравнения регрессии.

Для линейного уравнения множественной регрессии

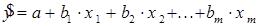
система нормальных уравнений имеет вид:

Для ее решения может быть применен метод исключения Гаусса.

Возможен и другой способ оценки параметров линейного уравнения множественной регрессии - через построение уравнения регрессии в стандартизированном масштабе.

При построении уравнения регрессии в стандартизированном масштабе все переменные переводятся в стандартизированные величины (так называемые «стандарты») по формулам:

, .

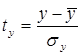Таким образом, начало отсчета каждой стандартизированной переменной совпадает с ее средним значением, а в качестве единицы измерения принимается ее среднее квадратическое отклонение.

Уравнение регрессии в стандартизированном масштабе имеет следующий вид:

.

Стандартизированные коэффициенты регрессии или b - коэффициенты определяются с помощью обычного метода наименьших квадратов.

При этом система нормальных уравнений будет иметь вид:

где - парные коэффициенты корреляции,

- парные коэффициенты межфакторной корреляции.

Стандартизированные коэффициенты регрессии показывают на сколько среднеквадратических отклонений (s_y) изменится результативный признак при изменении соответствующего фактора на одно среднеквадратическое отклонение (s_x) при неизменных значениях других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизированные коэффициенты регрессии b _i сопоставимы. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результативный признак. В этом основное достоинство стандартизированных коэффициентов регрессии в отличие от обычных коэффициентов регрессии b_i, которые несравнимы между собой.

Связь коэффициентов множественной регрессии b_i со стандартизированными коэффициентами b_i описывается соотношением

.

Параметр a определяется следующим образом

.

Для расширения аналитических возможностей и более подробной характеристики влияния факторов на результативный признак наряду с коэффициентами чистой регрессии b_i и b-коэффициентами в линейной множественной регрессии вычисляются частные коэффициенты детерминации, D- и Q-коэффициенты, а так же частные коэффициенты эластичности.

Частные коэффициенты детерминации характеризуют вклад каждого фактора в изменение результативной переменной и рассчитываются по формуле:

.

Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака обусловлена вариацией i-го фактора, входящего во множественное уравнение регрессии.

Сумма частных коэффициентов детерминации равна коэффициенту детерминации:

.

Чтобы оценить долю влияния каждого фактора в суммарном влиянии факторов, включенных в уравнение регрессии, вычисляют D -коэффициенты:

, .

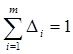Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменится значение результативного признака при изменении соответствующего фактора x_i на 1 процент при неизменном значении других факторов, зафиксированных на среднем уровне. В случае линейного уравнения регрессии частные коэффициенты эластичности не являются постоянными величинами, а зависят от значения соответствующего фактора

.

По этой причине, часто, на практике, используют средние частные коэффициенты эластичности:

.

Для более точной оценки влияния каждого фактора на результативный признак используют, также Q-коэффициенты, определяемые по формуле

,

где - коэффициент вариации i-го фактора

.

Q-коэффициенты характеризуют с одной силу влияния некоторого фактора на результат (через показатель эластичности), а с другой - возможность изменения этого фактора (посредством коэффициента вариации).

Для целенаправленного воздействия на какой либо экономический процесс следует использовать управляемые факторы имеющие максимальное значение модуля Q-коэффициента.

На основе линейного уравнения множественной регрессии могут быть найдены частные уравнения регрессии, связывающие результативный признак y с соответствующим фактором x_i при закреплении значений других учитываемых во множественной регрессии факторов на среднем уровне:

или

где

Таким образом, по внешнему виду частные уравнения регрессии похожи на парные уравнения регрессии. Однако в отличие от уравнений парной регрессии частные уравнения характеризуют изолированное влияние соответствующих факторов на результат.

Параметры нелинейных уравнений регрессии также определяются методом наименьших квадратов. В этом случае нелинейные уравнения множественной регрессии приводятся к линейному виду.

Так, параболическое уравнение множественной регрессии сводится к линейному путем введения новых переменных z_i

,

где .

Гиперболическое уравнение вида

сводится к линейному заменой зависимой переменной :

,

а гипербола вида

- заменой независимых переменных

.

Экспоненциальное уравнение регрессии

линеаризуется путем логарифмирования:

и последующей замены переменной :

.

Так же логарифмированием и заменой переменных приводится к линейному виду степенное уравнение множественной регрессии

:

,

,

где , , .