 |
Главная |
Математическое ожидание. Дисперсия и среднее квадратическое отклонение случайной величины
|
из
5.00
|
Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, выражающие наиболее характерные свойства (черты) закона распределения случайной величины. Такие числа носят название числовых характеристик случайной величины.
Математическим ожиданием (или средним значением) 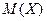 (или
(или  ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
Если дискретная случайная величина X принимает конечное число значений  , то ее математическое ожидание
, то ее математическое ожидание 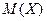 находится по формуле
находится по формуле
 (3)
(3)
Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то
 , (4)
, (4)
при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд 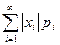 .
.
Математическое ожидание непрерывной случайной величины X с плотностью вероятности  , находится по формуле
, находится по формуле
 , (5)
, (5)
при этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл  ).
).
Дисперсией (рассеянием)  (или
(или 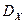 ) случайной величины
) случайной величины  называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
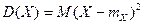 .
.
Из определения вытекает часто используемая формула:
 .
.
Если  -дискретная случайная величина, то ее дисперсия вычисляется по формуле:
-дискретная случайная величина, то ее дисперсия вычисляется по формуле:
 , (т. е.
, (т. е.  ) (6)
) (6)
в случае конечного числа значений, принимаемых случайной величиной X, и по формуле
 , (т. е.
, (т. е.  ) (7)
) (7)
в случае счетного числа значений.
Если X - непрерывная случайная величина сплотностью  , то
, то
 (или
(или  ). (8)
). (8)
Средним квадратическим отклонением случайной величины  называется величина
называется величина 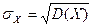 .
.
Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.
Мода и медиана
Кроме математического ожидания и дисперсии в теории вероятностей применяется еще ряд числовых характеристик, в частности, мода и медиана случайной величины.
Модой  дискретной случайной величины X называется ее наиболее вероятное значение.
дискретной случайной величины X называется ее наиболее вероятное значение.
Модой непрерывной случайной величины X называется такое ее значение  , при котором плотность распределения
, при котором плотность распределения  имеет максимум, т. е.
имеет максимум, т. е. 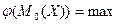 .
.
На рис. 3 и 4 показана мода для дискретной и непрерывной случайной величины.


Рис. 3 Рис. 4
Если многоугольник распределения (кривая распределения) имеет два или несколько максимумов, то распределение называется двухмодальным или многомодальным.
Иногда встречаются распределения, которые имеют минимум, но не имеют максимум. Такие распределения называются антимодальными.
Медианой непрерывной случайной величины X (обозначение:  ) называется такое ее значение
) называется такое ее значение  , для которого одинаково вероятно, окажется ли случайная величина
, для которого одинаково вероятно, окажется ли случайная величина  меньше
меньше  или больше
или больше  , т. е.
, т. е.
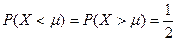 . (9)
. (9)
Геометрически вертикальная прямая  , проходящая через точку с абсциссой, равной
, проходящая через точку с абсциссой, равной  , делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна
, делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна  , т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке
, т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке  равна
равна  , т. е.
, т. е.  .
.

Рис. 5
Для дискретной случайной величины медиана обычно не определяется.
Решение задач
Пример 1.Производится три независимых опыта, в каждом из которых событие A появляется с вероятностью 0,4. Рассматривается случайная величина X – число появлений события A в трех опытах. Построить ряд и многоугольник распределения, функцию распределения случайной величины X. Найти: 1) вероятность событий: A={X<2}; B={  }; C={
}; C={ 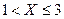 }; 2) математическое ожидание
}; 2) математическое ожидание  , дисперсию
, дисперсию 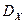 , среднее квадратическое отклонение
, среднее квадратическое отклонение  случайной величины X.
случайной величины X.
Решение.Случайная величина X может принимать значения  ;
;  ;
;  ;
;  . Соответствующие им вероятности
. Соответствующие им вероятности 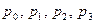 найдем, воспользовавшись формулой Бернулли. При n=3,
найдем, воспользовавшись формулой Бернулли. При n=3,  ;
;  имеем:
имеем:  ;
;  ;
;
 ;
;  .
.
Отсюда ряд распределения случайной величины X имеет вид:

(Контроль:  ).
).
Многоугольник распределения случайной величины X представлен на рис.6.


Рис. 6 Рис. 7
Найдем функцию распределения F(x). По определению функции распределения имеем: если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то
, то 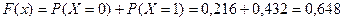 ;
;
если 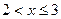 , то
, то  ;
;
если  , то
, то 
 .
.
Итак, 
График функции F(x) изображен на рис. 7.
1) Сначала вычислим искомые вероятности непосредственно:
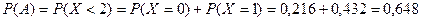 ;
;
 ;
;
 .
.
Эти же вероятности найдем, воспользовавшись формулами:
 и
и  . Тогда
. Тогда  ;
;
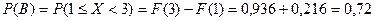 ;
;

2) Найдем математическое ожидание случайной величины X. Используя формулу (3), получим  . Вычислим дисперсию. По формуле (6) имеем:
. Вычислим дисперсию. По формуле (6) имеем:
 =0,72. Тогда среднее квадратическое отклонение
=0,72. Тогда среднее квадратическое отклонение  .
.
Пример 2.Дан ряд распределения дискретной случайной величины X:

Найти моду.
Решение.Так как дискретная случайная величина X принимает значение  с наибольшей вероятностью
с наибольшей вероятностью  по сравнению с двумя соседними значениями, то мода случайной величины X равна 20, т. е.
по сравнению с двумя соседними значениями, то мода случайной величины X равна 20, т. е.  .
.
Пример 3.Дана функция
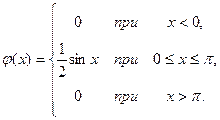
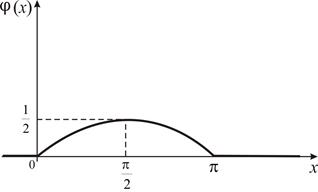
Рис. 8
Показать, что  может служить плотностью вероятности некоторой случайной величины X.. Найти математическое ожидание и дисперсию случайной величины X.
может служить плотностью вероятности некоторой случайной величины X.. Найти математическое ожидание и дисперсию случайной величины X.
Решение.Используя свойство нормированности плотности распределения, найдем, что
 ,
,
кроме того,  . Следовательно,
. Следовательно,  может служить плотностью вероятности некоторой случайной величины. Так как прямая
может служить плотностью вероятности некоторой случайной величины. Так как прямая  является осью симметрии соответствующей дуги кривой
является осью симметрии соответствующей дуги кривой  (см. рис.8), то математическое ожидание случайной величины X равно
(см. рис.8), то математическое ожидание случайной величины X равно  , т. е.
, т. е.  . Найдем дисперсию, воспользовавшись формулой (8). Двукратным интегрированием по частям получим:
. Найдем дисперсию, воспользовавшись формулой (8). Двукратным интегрированием по частям получим:

Пример 4.Дана плотность вероятности случайной величины X;

Найти функцию распределения F(X), вероятность попадания случайной величины X в промежуток  , числовые характеристики величины X:
, числовые характеристики величины X:  .
.
Решение.Найдем функцию распределения случайной величины X, для этого воспользуется соотношением (1).
Если x < 0, то  .
.
Если  , то
, то  .
.
Если x > a, то 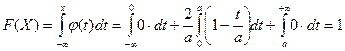 .
.
Итак, 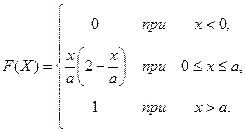
По формуле (*) имеем  .
.
Найдем математическое ожидание случайной величины X. Согласно формуле (5)
 .
.
Теперь отыщем дисперсию. По формуле (8)

Отсюда среднее квадратическое отклонение  .
.
Пример 5.Найти моду, медиану, математическое ожидание и функцию распределения случайной величины X с плотностью вероятности

Решение.Найдем точку максимума функции  :
:  ; отсюда
; отсюда  при
при  . Точка
. Точка  является точкой максимума функции
является точкой максимума функции  , так как
, так как  , если
, если  и
и 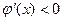 , если
, если  . Следовательно, мода
. Следовательно, мода  .
.
Медиану  определим из условия (9):
определим из условия (9):  (или
(или 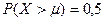 ).
).
В данном случае по формуле (2): 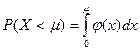 , т. е.
, т. е.  .
.
Таким образом, приходим к уравнению:  или
или  . Отсюда,
. Отсюда,  .
.
Воспользовавшись формулой (5), вычислим математическое ожидание случайной величины X:


Найдем функцию распределения случайной величины X.
Прежде всего заметим, что если x < 0, то 
Если же  то
то 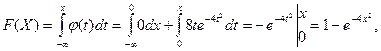 т. е.
т. е.  .
.
|
из
5.00
|
Обсуждение в статье: Математическое ожидание. Дисперсия и среднее квадратическое отклонение случайной величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

