Обратный ход метода Гаусса

Учреждение образования «Белорусская государственная

Сельскохозяйственная академия»

 

 

 

Кафедра высшей математики

 

Методические указания

по изучению темы «Метод Гаусса решения систем линейных

уравнений» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)

 

Горки, 2013

 

Метод Гаусса решения систем линейных уравнений

Эквивалентные системы уравнений

 

Две системы линейных уравнений называются эквивалентными, если каждое решение одной из них является решением другой. Процесс решения системы линейных уравнений состоит в последовательном преобразовании её в эквивалентную систему с помощью так называемых элементарных преобразований, которыми являются:

1) перестановка любых двух уравнений системы;

2) умножение обеих частей любого уравнения системы на отличное от нуля число;

3) прибавление к любому уравнению другого уравнения, умноженного на любое число;

4) вычёркивание уравнения, состоящего из нулей, т.е. уравнения вида .

 

Гауссовы исключения

 

Рассмотрим систему m линейных уравнений с n неизвестными:

Суть метода Гаусса или метода последовательного исключения неизвестных состоит в следующем.

Вначале с помощью элементарных преобразований исключается неизвестная из всех уравнений системы, кроме первого. Такие преобразования системы называются шагом гауссового исключения. Неизвестная называется разрешающей переменной на первом шаге преобразований. Коэффициент называется разрешающим коэффициентом, первое уравнение называется разрешающим уравнением, а столбец коэффициентов при разрешающим столбцом.

При выполнении одного шага гауссового исключения нужно пользоваться следующими правилами:

1) коэффициенты и свободный член разрешающего уравнения остаются неизменными;

2) коэффициенты разрешающего столбца, расположенные ниже разрешающего коэффициента, обращаются в нули;

3) все прочие коэффициенты и свободные члены при выполнении первого шага вычисляются по правилу прямоугольника:

, где i=2,3,…,m; j=2,3,…,n.

Аналогичные преобразования выполним и над вторым уравнением системы. Это приведёт к системе, у которой во всех уравнениях, кроме первых двух, будет исключена неизвестная . В результате таких преобразований над каждым из уравнений системы (прямой ход метода Гаусса) исходная система приводится к эквивалентной ей ступенчатой системе одного из следующих видов.

 

Обратный ход метода Гаусса

 

Ступенчатая система

имеет треугольный вид и все (i=1,2,…,n). Такая система имеет единственное решение. Неизвестные определяются, начиная с последнего уравнения (обратный ход метода Гаусса).

Ступенчатая система имеет вид

где , т.е. число уравнений системы меньше либо равно числу неизвестных. Эта система не имеет решений, так как последнее уравнение не будет выполняться ни при каких значениях переменной .

Ступенчатая система вида

имеет бесчисленное множество решений. Из последнего уравнения неизвестная выражается через неизвестные . Затем в предпоследнее уравнение вместо неизвестной подставляется её выражение через неизвестные . Продолжая обратный ход метода Гаусса, неизвестные можно выразить через неизвестные . В этом случае неизвестные называются свободными и могут принимать любые значения, а неизвестные базисными.

При практическом решении систем удобно выполнять все преобразования не с системой уравнений, а с расширенной матрицей системы, состоящей из коэффициентов при неизвестных и столбца свободных членов.

Пример 1. Решить систему уравнений

Решение. Составим расширенную матрицу системы и выполним элементарные преобразования:

.

В расширенной матрице системы число 3 (оно выделено) является разрешающим коэффициентом, первая строка является разрешающей строкой, а первый столбец – разрешающим столбцом. При переходе к следующей матрице разрешающая строка не изменяется, все элементы разрешающего столбца ниже разрешающего элемента заменяются нулями. А все другие элементы матрицы пересчитываются по правилу четырёхугольника. Вместо элемента 4 во второй строке запишем , вместо элемента -3 во второй строке будет записано и т.д. Таким образом, будет получена вторая матрица. У этой матрицы разрешающим элементом будет число 18 во второй строке. Для формирования следующей (третьей матрицы) вторую строку оставляем без изменения, в столбце под разрешающим элементом запишем нуль и пересчитаем оставшиеся два элемента: вместо числа 1 запишем , а вместо числа 16 запишем .

В результате исходная система свелась к эквивалентной системе

Из третьего уравнения находим . Подставим это значение во второе уравнение: 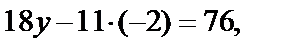y=3. В первое уравнение подставим найденные значения y и z: , x=2.

Таким образом, решением данной системы уравнений является x=2, y=3, .

Пример 2. Решить систему уравнений

Решение. Выполним элементарные преобразования над расширенной матрицей системы:

Во второй матрице каждый элемент третьей строки разделили на 2.

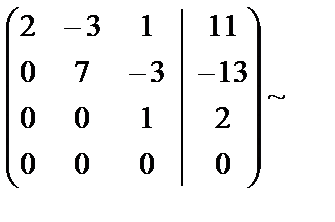
В четвёртой матрице каждый элемент третьей и четвёртой строки разделили на 11.

. Полученная матрица соответствует системе уравнений

Решая данную систему, найдём , , .

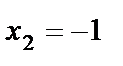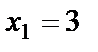Пример 3. Решить систему уравнений

Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования:

.

Во второй матрице каждый элемент второй, третьей и четвёртой строк разделили на 7.

В результате получена система уравнений

эквивалентная исходной.

Так как уравнений на два меньше, чем неизвестных, то из второго уравнения . Подставим выражение для в первое уравнение: , .

Таким образом, формулы дают общее решение данной системы уравнений. Неизвестные и являются свободными и могут принимать любые значения.

Пусть, например, 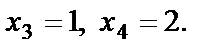Тогда и . Решение является одним из частных решений системы, которых бесчисленное множество.

 

Вопросы для самоконтроля знаний

 

1) Какие преобразования линейных систем называются элементарными?

2) Какие преобразования системы называются шагом гауссова исключения?

3) Что такое разрешающая переменная, разрешающий коэффициент, разрешающий столбец?

4) Какими правилами нужно пользоваться при выполнении одного шага гауссова исключения?