 |
Главная |
Нормальное уравнение плоскости
|
из
5.00
|
Плоскость и прямая в пространстве
Общее уравнение плоскости
Плоскость однозначно определяется точкой на плоскости и вектором, перпендикулярным к ней. Пусть точка Mo(x0,y0,z0) лежит на плоскости и вектор 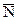 (A,B,C) перпендикулярен к плоскости (рис. 1)
(A,B,C) перпендикулярен к плоскости (рис. 1)

Возьмём на плоскости p любую точку M(x,y,z), образуем вектор 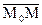 и используем условие перпендикулярности двух векторов
и используем условие перпендикулярности двух векторов 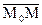 и
и 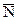 .
.
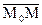 ^
^ 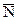 Þ (
Þ ( 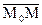 ,
, 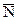 ) = 0 (1)
) = 0 (1)
Обозначим  радиусы векторы точек
радиусы векторы точек 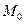 и
и 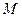 , соответственно
, соответственно 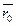 и
и  . Тогда уравнение (2) можно записать так:
. Тогда уравнение (2) можно записать так:  . (2)
. (2)
Получим векторное уравнение плоскости.
Запишем левое уравнение (2) в координатной форме.
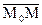 =(x0-x, y0-y, z-z0),
=(x0-x, y0-y, z-z0), 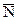 =(A, B, C)
=(A, B, C) 
(  ,
, 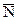 ) = 0
) = 0 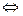 A(x-x0) + B(y0-y) + C(z-z0)=0 (3)
A(x-x0) + B(y0-y) + C(z-z0)=0 (3)
Запишем правое уравнение (2) в координатной форме: 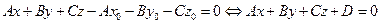 , (4)
, (4)
где 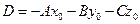 .
.
Уравнение (4) называется общим уравнением плоскости в пространстве, а уравнение (3) – уравнением прямой, проходящей через данную точку.
Рассмотрим, в чём заключаются особенности расположения плоскости, заданной общим уравнением Ax+By+Cz+D=0, если некоторые коэффициенты этого уравнения обращаются в нуль.
1. A=0. В этом случае вектор N=Bj+Ck; он компланарен ортам j и k, т.е. параллелен плоскости Oyz, поэтому соответствующая плоскость будет параллельна оси Ox.
Аналогично, если B = 0, то плоскость параллельна оси Oy, если С = 0, то плоскость параллельна оси Oz.
2. D=0. Плоскость проходит через начало координат.
3. A=0, B=0 Þ плоскость параллельна плоскости Oxy (перпендикулярна оси Oz); уравнение такой плоскости приводится к виду z = c.
Аналогично, если A=C=0, то плоскость перпендикулярна оси Oy; если B=C=0, то плоскость перпендикулярна оси Ox. Уравнения таких плоскостей приводится соответственно к виду y = b; x = a.
4. A=D=0. Плоскость проходит через ось Ox, поскольку она параллельна оси Ox(A=0) и проходит через начало координат (D=0).
Аналогично, если B=D=0, то плоскость проходит через ось Oy. Если C=D=0, то плоскость проходит через ось Oz.
5. A=B=D=0. Плоскость совпадает с плоскостью Oxy, её уравнение z = 0.
A=C=D=0. Плоскость совпадает с плоскостью Oxz, её уравнение z = 0.
B=C=D=0. Плоскость совпадает с плоскостью Oyz, её уравнение x = 0.
Уравнение в отрезках
Пусть в уравнении Ax+By+Cz+D = 0 , A¹0 , B¹0 , C¹0 , D¹0,
т.е. плоскость пересекает все три оси координат и не проходит через начало.
Преобразуем уравнение следующим образом: Ax + By + Cz = -D
 , обозначив a = (-D/A); b = (-D/B); c = (-D/C), будем иметь
, обозначив a = (-D/A); b = (-D/B); c = (-D/C), будем иметь
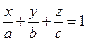 (5)
(5)
Уравнение (5) называется уравнением плоскости в отрезках.
Нормальное уравнение плоскости
Пусть в пространстве заданы система прямоугольных декартовых координат и некоторая плоскость p (рис. 2), положение которой определено единичным вектором  , имеющим направление перпендикуляра OD, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра.
, имеющим направление перпендикуляра OD, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра. 
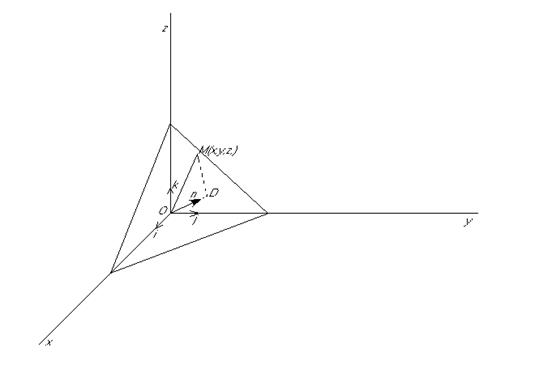
Рис. 2
Произвольную точку плоскости М мы будем обозначать двояким образом: либо при помощи её координат в виде M(x,y,z), либо при помощи её радиус-вектора – в виде  =
= 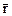 ; оба способа равнозначны, поскольку
; оба способа равнозначны, поскольку 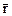 =x
=x 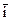 + y
+ y  + z
+ z 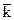 .
.
При любом положении точки М на плоскости p проекция её радиуса вектора 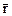 на направление вектора
на направление вектора  всегда равна p:
всегда равна p: 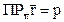 . Но это равенство можно записать используя скалярное произведение.
. Но это равенство можно записать используя скалярное произведение.
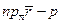 = (r,n) - p = 0 (6)
= (r,n) - p = 0 (6)
Это также векторное уравнение плоскости p.
От векторного уравнения перейдём к её координатному уравнению.
Обозначим через a, b, g углы образованные единичным вектором  с ортами
с ортами 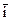 ,
,  ,
, 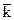 . Тогда cosa, cosb и cosg будут координатами этого вектора:
. Тогда cosa, cosb и cosg будут координатами этого вектора:
 =
= 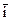 cosa +
cosa +  cosb +
cosb + 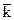 cosg (7)
cosg (7)
Кроме того, известно, что 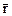 = x
= x 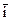 + y
+ y  + z
+ z 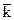 (8)
(8)
Выразим ( 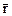 -
-  ) - p = 0 в координатной форме:
) - p = 0 в координатной форме:
( 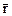 ,
,  ) - p = x cosa + y cosb + z cosg – p = 0 (9)
) - p = x cosa + y cosb + z cosg – p = 0 (9)
Это нормальное уравнение плоскости в координатной форме.
Пусть теперь дано какое-нибудь уравнение плоскости p: Ax + By + Cz + D = 0 (10)
Как, отправляясь от этого уравнения, получить нормальное уравнение той же плоскости?
Так как уравнения (6) и (7) определяют одну и ту же плоскость p, то их соответствующие коэффициенты пропорциональны, т.е.
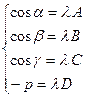 (11)
(11)
при некотором l, из равенств (11) определяем l: ôlô= 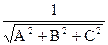 (9)
(9)
Знак l определяем для случая D¹0 из четвёртого равенства (11); так как p>0, то lD<0 и, следовательно, l имеет знак, противоположный знаку D.
Определение: Число l, имеющее модуль 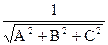 и знак, противоположный знаку коэффициента D, называется нормирующим множителем уравнения (10). При D=0 можно знак l выбрать произвольно.
и знак, противоположный знаку коэффициента D, называется нормирующим множителем уравнения (10). При D=0 можно знак l выбрать произвольно.
Мы установили: для того, чтобы из общего уравнения плоскости (10) получить нормальное уравнение плоскости (9), надо обе части уравнения (10) умножить на нормирующий множитель этого уравнения.
|
из
5.00
|
Обсуждение в статье: Нормальное уравнение плоскости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

