Е) график функции распределения

1)Из ящика, содержащего 2 бракованных и 4 годных детали, наугад извлекают 4 детали. число вынутых годных деталей. Найти .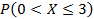

2)В колоде осталось 7 карт, из них 3 козырных. Наугад выбирают 4 карты. число взятых козырных карт. Найти вероятность того, что козырных карт будет не менее одной среди выбранных.

3)Из каждой партии телевизоров для контроля извлекают 4 телевизора и последовательно их проверяют. При появлении плохо работающего телевизора бракуется вся партия. Пусть количество проверенных телевизоров до появления бракованного, а вероятность брака равна 0,2. Найти .

4)Котировки акций могут быть размещены в Интернете на трех сайтах. Материал есть на первом сайте с вероятностью 0,7, на втором – с вероятностью 0,6, на третьем – 0,8. Студент переходит к новому сайту только в том случае, если не найдет данных на предыдущем. Пусть число сайтов, которые посетит студент. Какова вероятность того, что студент посетит меньше трех сайтов?

5)В цехе имеется 5 однотипных станков. Вероятность выхода из строя одного станка равна 0,8. число станков, потребовавших ремонта. Найти .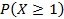

6)В тесто кладется изюм из расчета четыре изюминки на булку. Покупатель приобретает 2 булки. суммарное число изюма в купленных булках. Найти вероятность того, что в купленной булке не больше трех изюминок. Сколько изюма надо класть в тесто, чтобы вероятность иметь хотя бы одну изюминку в булке была не меньше 0,8?

7)Имеется 9 радиоламп, среди которых 3 неисправных. Наугад берутся 4 радиолампы и проверяются на годность. число неисправных радиоламп. Найти .

8)Производятся последовательные испытания 5 приборов, причем испытания прекращаются сразу после того, как проверяемый прибор оказался надежным. Вероятность выдержать испытание для каждого прибора равна 0,8. число испытаний, после которых закончится проверка. Какова вероятность того, что испытания не пройдут более, чем 3 прибора?

9)Производится тестирование 5 больших интегральных схем (БИС). Вероятность того, что БИС неисправна, равна 0,6. число неисправных БИС. Найти .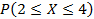

10)Пусть число очков, выпавших при бросании двух игральных костей. Найти вероятность того, что суммарное число очков будет ровно 10.

11)Пусть число гербов, полученных при бросании трех монет. Найти .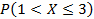

12)В ящике 100 шаров, из них 20 синих, 30 черных и 50 красных. Шар вынимают наугад, фиксируют его цвет и возвращают его в ящик. Проводится 6 таких испытаний. число вынутых черных шаров в этих испытаниях. Найти .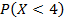

13)В ящике содержится 7 стандартных и 3 бракованных детали. Вынимают детали последовательно до появления стандартной, не возвращая их обратно. число извлеченных бракованных деталей. Найти

14)При бросании двух игральных костей игрок выигрывает 25 руб., если на обеих костях выпадает по 6 очков; 3 руб. – если на одной кости выпало 6 очков; 1 руб. – если сумма выпавших очков равна 6. размер выигрыша, возможный при одном бросании. Какова вероятность того, что сумма выигрыша составит не менее 2 рублей?

15)В первой урне содержится 3 белых и 5 черных шаров, во второй урне – 6 белых и 4 черных шара, в третьей урне – 1 белый и 3 черных шара. Из каждой урны вынимают по 1 шару. число извлеченных черных шаров. Найти

16)В группе из 5 изделий имеется 1 бракованное. Чтобы его обнаружить, выбирают наугад одно изделие за другим и проверяют. число извлеченных деталей до обнаружения бракованной. Найти вероятность того, что число извлеченных деталей до обнаружения бракованных составит не менее 2.

17)На карточках записаны двузначные числа от 31 до 60. Карточку извлекают из урны, фиксируют, возвращают в урну и тщательно перемешивают. число карточек с цифрой 5 в серии из 4 таких испытаний. Найти

18)Из урны, содержащей 2 белых и 3 черных шара, вынимается шар, записывается его цвет и возвращается обратно. Опыт повторяется 5 раз. число появления белого шара. Найти вероятность того, что это число будет не меньше 2.

19)Имеется 5 патронов. По мишени ведутся выстрелы до первого попадания или пока не будут израсходованы все патроны. число израсходованных патронов. Вероятность попадания при каждом выстреле равна 0,6. Найти

20)Блок состоит из четырех независимо функционирующих элементов. Вероятность безотказной работы каждого элемента в течение определенного периода равна 0,9. число безотказно работающих элементов блока. Найти вероятность безотказной работы хотя бы одного элемента.

21)В партии, состоящей из 10 деталей, имеется 4 бракованных. Наугад извлекают 3 детали. число бракованных деталей среди 3 выбранных. Найти

22)Вероятность того, что трамвай подойдет к остановке строго по расписанию, равна 0,7. число трамваев, прибывших по расписанию, из 4 исследуемых. Какова вероятность того, что не больше 3 трамваев придет к остановке по расписанию?

23) число попаданий при четырех выстрелах, если вероятность промаха при каждом выстреле 0,6. Найти вероятность того, что будет не менее трех попаданий.

24)В среднем около 20% клиентов, обратившихся в фирму «Турсервис», оказываются недовольными уровнем обслуживания в этой фирме. число недовольных среди трех случайным образом выбранных клиентов. Найти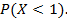

25)В тесто кладется изюм из расчета три изюминки на булку. Покупатель приобретает 2 булки. суммарное число изюма в купленных булках. Найти вероятность того, что в купленной булке нет ни одной изюминки. Сколько изюма надо класть в тесто, чтобы вероятность иметь хотя бы одну изюминку в булке была не меньше 0,99?

26)На связке пять различных ключей, ровно один из которых подходит к замку. Некто по очереди вставляет ключи в замок до тех пор, пока не откроет дверь (не подошедшие ключи откладываются в сторону). Пусть число попыток. Найти вероятность того, что этот некто откроет дверь не раньше, чем с третьей попытки.

27)По сети независимо друг от друга передаются четыре сообщения. Вероятность передачи каждого без искажения равняется 0,7. числа сообщений, переданных без искажения. Найти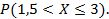

28)Каждый из четырех проверяемых студентов выполняет упражнения на тренажере с вероятностью 0,75. число студентов, выполнивших упражнение на тренажере. Найти вероятность того, что не менее двух студентов выполняет упражнение.

29)Три стрелка независимо один от другого стреляют по одному разу по одной и той же мишени. Вероятность попадания для каждого стрелка соответственно равны 0,7; 0,5; 0,1. число попаданий в мишень. Найти

30)Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует внимание рабочего равна для первого – 0,9; для второго – 0,8; для третьего – 0,75. число станков, которые не потребуют внимание рабочего в течение часа. Найти вероятность того, что хотя бы один станок не потребует внимания рабочего.

Задачи, пробные тесты

Типовой вариант контрольного материала:

1. Пусть вероятность того, что стрелок при стрельбе по спортивной мишени выбьет 10 очков равна 0,4; 9 очков – 0,2; 7 очков – 0,1; 6 очков – 0,1. Составить закон распределения случайной величины Х – числа выбитых стрелком очков. Составить интегральную функцию распределения и построить ее график. Вычислить мат.ожидание, Р(7≤ Х ≤10) и вероятность того, что стрелок выбьет более 7 очков.

2. Дифференциальный закон распределения непрерывной случайной величины Х задан графиком:

у

х

Записать аналитическое выражение дифференциального закона распределения случайной величины Х. Найти мат.ожидание и дисперсию случайной величины. Вычислить Р(2<Х<2,5).

Случайная величина Х распределена нормально с математическим ожиданием a = 25. Вероятность попадания Х в интервале (10, 15) равна 0,2. Чему равна вероятность попадания Х в интервал (35, 40)?

 

(примеры решения типовых задач см приложение 1)

(таблицы, схемы, рисунки см. приложение 2)