Краткие теоретические сведения. В Haskell списки являются гомогенными структурами данных

Списки

В Haskell списки являются гомогенными структурами данных. Они хранят несколько элементов одного типа. Это означает, что можно работать со списком целых чисел или списком символом, но нельзя иметь список, включающий несколько целых чисел и несколько символов. Списки заключаются в квадратные скобки, а элементы разделяются запятыми: [1,2,3,4,5].

 

Примечание. Можно использовать ключевое слово let для определения имени прямо в GHCi. Запись let a = 1 в GHCi эквивалентна записи a = 1 в загруженном скрипте.

 

Следует отметить, что строки — это списки символов. "hello" — это синтаксический сахар для ['h','e','l','l','o']. Поскольку строки являются списками, к ним можно применять любые функции для работы со списками.

Стандартная задача — объединение списков. Для этого предназначен оператор ++.

 

ghci> [1,2,3,4] ++ [9,10,11,12] [1,2,3,4,9,10,11,12] ghci> "hello" ++ " " ++ "world" "hello world" ghci> ['w','o'] ++ ['o','t'] "woot"

 

Для добавления одного элемента в начало списка используется оператор cons :.

 

ghci> 'A':" SMALL CAT" "A SMALL CAT" ghci> 5:[1,2,3,4,5] [5,1,2,3,4,5]

 

[], [[]], [[],[],[]] — разные списки. Первый представляет собой пустой список, второй — список, содержащий один пустой список, а третий — список, содержащий три пустых списка. Пустая строка, записываемая как "", эквивалентна пустому списку [].

Для получения некоторого элемента списка используется операция !!. Индексация начинается с нуля.

 

ghci> "Johnny Depp" !! 7 'D' ghci> [9.4,33.2,96.2,11.2,23.25] !! 1 33.2

 

Попытка получить, например, пятый элемент в трехэлементном списке приведет к ошибке.

Списки также могут содержать другие списки, которые состоят из списков, элементами которых являются списки...

 

ghci> let b = [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]] ghci> b [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]] ghci> b ++ [[1,1,1,1]] [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3],[1,1,1,1]]

 

Списки внутри списка могут быть различной длины, но они не могут быть различных типов. Так же, как нельзя иметь список, содержащий несколько чисел и несколько символов, нельзя иметь и список, содержащий несколько списков символов и несколько списков чисел.

Списки можно сравнивать, если сравнимы содержащиеся в них элементы. Если используются операторы <, <=, > и >=, списки сравниваются в лексикографическом порядке. Сначала сравниваются первые элементы. Если они равны, сравниваются вторые элементы, и так далее.

 

ghci> [3,2,1] > [2,1,0] True ghci> [3,4,2] == [3,4,2] True

 

Функции для работы со списками

Ниже перечислены базовые функции для работы со списками:

● head принимает список и возвращает его первый элемент (голову);

● tail принимает список и возвращает его хвост, то есть все элементы, за исключением головы;

● last принимает список и возвращает его последний элемент;

● init принимает список и возвращает всё, кроме его последнего элемента;

● length принимает список и возвращает его длину;

● null проверяет, является ли список пустым. Она возвращает True при пустом аргументе, иначе результат — False;

● reverse обращает список (меняет порядок элементов на обратный);

● take принимает число и список и извлекает указанное число элементов из начала списка;

● drop работает похожим образом, только отбрасывает указанное число элементов из начала списка;

● maximum принимает список, содержимое которого может быть расположено в некотором порядке, и возвращает максимальный элемент;

● minimum возвращает наименьший элемент списка;

● sum принимает список чисел и возвращает их сумму;

● product принимает список чисел и возвращает их произведение;

● elem принимает элемент и список элементов и проверяет, является ли первый аргумент элементом списка.

При использовании первых четырех функций нужно следить за тем, чтобы параметр не был пустым списком, иначе будет сгенерирована ошибка.

 

ghci> let xs = [1,2,3,4,5,6] ghci> head xs ghci> tail xs [2,3,4,5,6] ghci> last xs ghci> init xs [1,2,3,4,5] ghci> length xs ghci> null xs False ghci> reverse xs [6,5,4,3,2,1] ghci> take 3 xs [1,2,3] ghci> drop 4 xs [5,6] ghci> maximum xs ghci> minimum xs ghci> sum xs ghci> product xs ghci> 7 `elem` xs False

 

Диапазоны

Диапазоны — это способ создания списков, являющихся арифметическими последовательностями, которые могут быть перечислены.

Для того, чтобы создать, например, список, содержащий все натуральные числа от 1 до 20, необходимо написать [1..20].

 

ghci> [1..20] [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] ghci> ['a'..'z'] "abcdefghijklmnopqrstuvwxyz" ghci> ['K'..'Z'] "KLMNOPQRSTUVWXYZ"

 

В диапазонах можно задавать шаг. Необходимо просто разделить первые два элемента запятыми, а затем указать верхний предел. Следует соблюдать осторожность при использовании в диапазонах чисел с плавающей точкой, потому что они не совсем точные (по определению).

 

ghci> [2,4..20] [2,4,6,8,10,12,14,16,18,20] ghci> [3,6..20] [3,6,9,12,15,18] ghci> [0.1, 0.3 .. 1] [0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999]

 

Диапазоны можно также использовать для создания бесконечных списков, просто не определяя верхний предел. Очень часто к бесконечным спискам применяется функция take.

Существует несколько полезных функций, производящих бесконечные списки.

cycle принимает список и зацикливает его в бесконечный список. Для того, чтобы увидеть результат, уйдет вечность, поэтому следует в каком-нибудь месте обрезать список.

 

ghci> take 10 (cycle [1,2,3]) [1,2,3,1,2,3,1,2,3,1]

 

repeat принимает элемент и производит бесконечный список из одного этого элемента.

 

ghci> take 10 (repeat 5) [5,5,5,5,5,5,5,5,5,5]

 

Если необходимо некоторое количество одинаковых элементов в списке, проще использовать функцию replicate. replicate 3 10 вернет [10,10,10].

Выражения списков

В курсе математики рассматривается запись для выражения множества. Она обычно используется для построения более специфических множеств на основе более общих множеств. Простое выражение для множества, которое содержит первые 10 четных натуральных чисел, выглядит следующим образом: .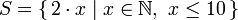

Часть до вертикальной линии называется производящей функцией, x — переменная, N — входное множество, x <= 10 — предикат. Это означает, что множество содержит удвоенные значения натуральных чисел, которые удовлетворяют предикату.

На Haskell такой список можно записать следующим образом:

 

ghci> [x * 2 | x <- [1..10]] [2,4,6,8,10,12,14,16,18,20]

 

Теперь добавим к выражению условие (или предикат). Предикаты располагаются после связывающей (присваивающей) части и отделяются от нее запятой. Допустим, нам нужны только такие элементы, которые (удвоенные) больше или равны 12.

 

ghci> [x * 2 | x <- [1..10], x * 2 >= 12] [12,14,16,18,20]

 

Определим список чисел от 50 до 100, чей остаток от деления на 7 равен 3.

 

ghci> [x | x <- [50..100], x `mod` 7 == 3] [52,59,66,73,80,87,94]

 

Отсев элементов списка предикатами также называется фильтрацией. Элемент включается в список, только если все предикаты возвращают True. Создадим выражение, которое заменяет в списке каждое нечетное число меньше 10 на "BANG!", а каждое нечетное число больше 10 — на "BOOM!". Если число четное, то мы его исключаем из списка. Для удобства поместим это выражение в функцию, чтобы его легко можно было использовать повторно.

 

boomBangs xs = [if x < 10 then "BOOM!" else "BANG!" | x <- xs, odd x]

 

ghci> boomBangs [7..13] ["BOOM!","BOOM!","BANG!","BANG!"]

 

Кроме того, что в выражении списка можно задавать несколько предикатов (элемент должен удовлетворять все предикаты для того, чтобы быть включенным в список), можно также использовать несколько входных списков. При использовании элементов из нескольких списков выражение списка порождает все возможные комбинации элементов заданных списков, а затем объединяет их по указанной производящей функции. Список, образованный выражением, использующим элементы двух списков по 4 элемента каждый, будем иметь длину 16, если не задать фильтрацию. Если у нас есть два списка [2,5,10] и [8,10,11] и мы хотим получить произведения всех возможных комбинаций между числами этих списков, можно использовать следующий код:

 

ghci> [x * y | x <- [2,5,10], y <- [8,10,11]] [16,20,22,40,50,55,80,100,110]

 

Можно написать собственную версию функции length.

 

length' xs = sum [1 | _ <- xs]

 

Символ _ означает, что для нас не имеет значения, какой элемент мы получаем из списка, поэтому вместо написания имени переменной, которую мы не будем никогда использовать, используется _.

Кортежи

В некотором смысле кортежи подобны спискам: они позволяют хранить несколько значений, как одно значение. Однако, между ними есть несколько фундаментальных различий. Список чисел хранит только числа. Это его тип, и не имеет значения то, сколько он хранит чисел: одно или бесконечное количество. Кортежи, в отличие от списков, используются тогда, когда точно известно, сколько значений нужно объединить, и тип кортежа зависит от того, сколько он включает компонентов, какие они имеют типы и в каком порядке они расположены. Кортежи заключаются в круглые скобки, а их компоненты разделяются запятыми.

Кортежы, как и данные других типов, можно заключать в списки: [(1,2),(8,11),(4,5)]. А запись [(1,2),(8,11,5),(4,5)] приведет к ошибке, потому что в одном списке нельзя хранить данные разных типов, а тут мы комбинируем пары с тройкой, которые являются разными типами данных.

Кортежи следует использовать, когда заранее известно, сколько компонентов должен содержать некоторый кусок данных. Кортежи менее гибки, поскольку кортежи разной длины соответствуют разным типам данных, поэтому нельзя написать общую функцию для присоединения элемента к кортежу — нужно иметь отдельную функцию для добавления элемента к паре, отдельную — к тройке, отдельную — к четырехэлементному кортежу и т.д.

В то время как существуют одноэлементные списки, нет такого понятия, как одноэлементный кортеж. Если подумать, в этом действительно нет смысла. Одноэлементный кортеж был бы просто отдельным значением, и от использования такого кортежа не было бы никакой выгоды.

Как и списки, кортежи можно сравнивать друг с другом, если сравнимы их компоненты. Нельзя только сравнивать два кортежа, имеющих разные типы. Далее рассмотрим две полезные функции, которые оперируют парами (только парами):

● fst принимает пару и возвращает ее первый компонент;

● snd принимает пару и возвращает ее второй компонент.

 

ghci> fst (8,11) ghci> snd (8,11)

 

Функция zip принимает два списка и сцепляет их в один список путем объединения соответствующих элементов в пары:

 

ghci> zip [1,2,3,4,5] [5,5,5,5,5] [(1,5),(2,5),(3,5),(4,5),(5,5)]

 

Если длины списков не совпадают, более длинный список просто обрежется до длины более короткого.

Типы данных

Haskell характеризуется статической типизацией данных. Тип каждого выражения известен во время компиляции, что ведет к более безопасному коду. Если попытаться написать программу, в которой будет выполняться деление булева значения на какое-то число, она даже не скомпилируется. Также Haskell обладает возможностью вывода типов. Если записать число, не нужно указывать ему на то, что это число. Haskell может это вывести самостоятельно, поэтому не нужно явно записывать типы функций и выражений.

Тип — это нечто, похожее на ярлык, который имеет каждое выражение. Он говорит о том, к какой категории вещей относится выражение. Выражение True — это булево значение, "hello" — строка и т.д.

Для получения типов выражений можно использовать GHCi. Для этого используется команда :type (или ее сокращенная форма :t) с указанием выражение, тип которого нужно получить.

 

ghci> :t 'a' 'a' :: Char ghci> :t True True :: Bool ghci> :t "HELLO!" "HELLO!" :: [Char] ghci> :t (True, 'a') (True, 'a') :: (Bool, Char) ghci> :t 4 == 5 4 == 5 :: Bool

 

Выполнение команды :t над выражением приводит к выводу этого выражения, за которым следует :: и его тип. :: читается как “имеет тип”. Явные типы всегда обозначаются первой буквой в верхнем регистре.

Функции также имеют типы. При определении функции можно явно задать ее тип. Это обычно считается хорошей практикой, за исключением написания коротких функций.

 

removeNonUppercase :: [Char] -> [Char] removeNonUppercase st = [c | c <- st, c `elem` ['A'..'Z']

 

Функция removeNonUppercase имеет тип [Char] -> [Char], означающий, что она производит отображение из строки в строку, поскольку она принимает одну строку в качестве параметра и возвращает другую строку как результат. Тип [Char] является синонимом String, поэтому будет более понятно, если записать так: removeNonUppercase :: String -> String. Нам необязательно задавать для этой функции определение типа, поскольку компилятор самостоятельно может вывести, что она принимает строку и возвращает строку, но мы всё равно сделали это. А как записать тип функции, которая принимает несколько параметров? Рассмотрим простую функцию, которая принимает три целых числа и складывает их.

 

addThree :: Int -> Int -> Int -> Int addThree x y z = x + y + z

 

Параметры разделены символами ->, и нет никаких особых различий между типами аргументов и типом результата. Тип результата — это последний компонент в определении, а типы аргументов — первые три.

Функции являются выражениями, поэтому команда :t работает с ними без проблем.

Рассмотрим подробнее некоторые наиболее распространенные типы.

Int обозначает целое число. Он используется для целых чисел. 7 может быть типа Int, а 7.2 — нет. Тип Int ограничен. Это означает, что он имеет минимальное и максимальное значение. Обычно на 32-битных машинах минимальным целым числом типа Int является -2147483648, а максимальным — 2147483647.

Integer также обозначает целое число. Главное его отличие от предыдущего типа заключается в том, что он неограничен, поэтому может использоваться для представления действительно больших целых чисел. Int, однако, более эффективен.

 

factorial :: Integer -> Integer factorial n = product [1..n]

 

ghci> factorial 50

 

Float обозначает число с плавающей точкой одинарной точности.

 

circumference :: Float -> Float circumference r = 2 * pi * r

 

ghci> circumference 4.0 25.132742

 

Double обозначает число с плавающей точкой двойной точности.

 

circumference' :: Double -> Double circumference' r = 2 * pi * r

 

ghci> circumference' 4.0 25.132741228718345

 

Bool — булев тип. Он имеет только два возможных значения: True и False.

Char используется для представления символа. Он заключается в одинарные кавычки. Список символов является строкой.

Тип кортежа зависит от его длины, типов его компонентов и порядка из следования, поэтому теоретически существует бесконечное множество типов кортежей. Следует отметить, что пустой кортеж () — это также тип, который может иметь только одно значение: ().

Переменные типов

Узнаем тип функции head:

 

ghci> :t head head :: [a] -> a

 

a — это переменная типа. Это означает, что a может быть любого типа. Функции, которые содержат переменные типов, называются полиморфными. Определение типа функции head говорит о том, что она принимает список любого типа и возвращает один элемент этого типа.

Хотя переменные типов могут иметь имена, состоящие более чем из одного символа, обычно используют имена a, b, c, d...

Классы типов

Класс типов — это что-то вроде интерфейса, который определяет некоторое поведение. Если тип является частью класса типов, это означает, что он поддерживает и реализует поведение, которое описывает класс типов.

Рассмотрим сигнатуру функции ==?

 

ghci> :t (==) (==) :: Eq a => a -> a -> Bool

 

Здесь можно увидеть новый символ =>. Всё, что находится до символа =>, называется ограничением класса. Предыдущее определение типа можно прочитать следующим образом: функция равенства принимает два любых значения одного типа и возвращает результат типа Bool. Тип этих двух значений должен быть членом класса Eq (это было ограничением класса).

Рассмотрим некоторые базовые классы типов.

Eq используется для классов, которые поддерживают проверку на равенство. Его члены реализуют функции == и /=. Так что если в функции существует ограничение класса Eq для переменной типа, она может использовать == или /= в своем определении. Все ранее упомянутые типы, за исключением функций, являются частью Eq, поэтому могут быть проверены на равенство.

Ord используется для типов, которые поддерживают упорядочение. Все ранее рассмотренные типы, кроме функций, являются частью Ord. Ord покрывает стандартные функции сравнения, такие как >, <, >= и <=. Функция compare принимает два члена Ord одного типа и возвращает отношение порядка между ними. Ordering — это тип, который имеет значения GT, LT и EQ, которые означают больше чем, меньше чем и равно. Для того, чтобы быть членом Ord, тип должен быть также членом класса Eq.

Члены класса Show могут быть представлены как строки. Все изученные ранее типы, кроме типов функций, являются частью Show. Наиболее используемой функцией, которая работает с классом Show, является show. Она принимает значение, чей тип является членом Show, и представляет его как строку.

 

ghci> show 3 "3" ghci> show 5.334 "5.334" ghci> show True "True"

 

Read — это класс типов, в какой-то степени противоположный классу Show. Функция read принимает строку и возвращает значение типа, являющегося членом класса Read.

 

ghci> read "True" || False True ghci> read "8.2" + 3.8 12.0 ghci> read "5" - 2 ghci> read "[1,2,3,4]" ++ [3] [1,2,3,4,3]

 

Опять же, все ранее рассмотренные типы входят в этот класс. Но если просто записать read "4", сгенерируется ошибка. GHCi выведет сообщение о том, что не знает, что именно мы хотим получить в результате. В предыдущих случаях использования функции read мы производили над ее результатом некоторые действия, поэтому GHCi мог вывести тип результата. Но если мы не используем результат в дальнейшем, у GHCi не будет возможности выяснить тип. Для таких случаев можно использовать аннотации типов. Аннотации типов являются способом явного задания того, какой тип должно иметь выражение. Делается это добавлением :: к концу выражения и указанием типа.

 

ghci> read "5" :: Int ghci> read "5" :: Float 5.0 ghci> (read "5" :: Float) * 4 20.0 ghci> read "[1,2,3,4]" :: [Int] [1,2,3,4] ghci> read "(3, 'a')" :: (Int, Char) (3, 'a')

 

Члены Enum — последовательно упорядоченные типы, они могут быть перечислены. Главное преимущество класса типов Enum состоит в том, что его типы можно использовать в диапазонах списков. Для них также определены последователи и предшественники, которые можно получить функциями succ и pred. В этот класс входят следующие типы: (), Bool, Char, Ordering, Int, Integer, Float и Double.

Члены класса Bounded имеют верхние и нижние границы.

 

ghci> minBound :: Int -2147483648 ghci> maxBound :: Char '\1114111' ghci> maxBound :: Bool True ghci> minBound :: Bool False

 

Функции minBound и maxBound очень интересны, потому что имеют тип Bounded a => a. В этом смысле они являются полиморфными константами.

Все кортежи также являются частью класса Bounded, если компоненты также входят в него.

Num — числовой класс типов. Его члены могут вести себя, как числа. К нему относятся типы Int, Integral, Float и Double. Для того, чтобы присоединиться к классу типов Num, тип также должен входить в классы типов Show и Eq.

Integral также является числовым классом типов. Num включает все числа: как целые, так и вещественные. Integral включает только целые числа. В него входят типы Int и Integer.

Floating включает только числа с плавающей точкой (Float и Double).

Очень полезная функция для работы с числами — fromIntegral. Она имеет следующее определение типа: fromIntegral :: (Integral a, Num b) => a -> b. Из ее сигнатуры видно, что она принимает целое число и переводит его в более общее число. Это полезно, когда нужно, чтобы целые и вещественные числа работали вместе без проблем.

Содержание отчета

1. Титульный лист с указанием названия лабораторной работы.

2. Цель работы.

3. Номер варианта.

4. Задание.

5. Исходный код разработанных функций.

6. Результаты тестирования разработанных функций.

Варианты заданий

Все функции можно определить в одном файле с произвольным именем. Для каждой функции обязательно указать определение типа.

Вариант 1

1. Определить функцию, принимающую в качестве аргумента список целых чисел и возвращающую список сумм цифр двузначных элементов входного списка.

2. Определить функцию, принимающую на вход целое число и возвращающую квадраты чисел, находящихся в диапазоне от 1 до 100 и кратных введенному, в виде списка.

3. Определить функцию, принимающую в качестве аргумента список пар чисел и символ. Если введенный символ равен ‘a’, то вернуть список сумм компонентов каждой пары. Если введенный символ равен ‘s’, то вернуть список разностей первого и второго компонента каждой пары. В противном случае вернуть список произведений компонентов каждой пары.

Вариант 2

1. Определить функцию, принимающую в качестве аргумента список чисел и возвращающую список удвоенных значений элементов списка, кратных его голове.

2. Определить функцию, принимающую на вход список чисел и целое число и возвращающую список чисел, в котором указанное число первых элементов удваивается, а остальные элементы утраиваются.

3. Определить функцию, принимающую в качестве аргумента две пары, соответствующие комплексным числам в формате (<действительная часть>,<мнимая часть>). Результат функции — произведение введенных комплексных чисел.

Вариант 3

1. Определить функцию, принимающую в качестве аргумента список целых чисел и возвращающую в качестве результата произведение нечетных элементов списка.

2. Определить функцию, принимающую на вход два целых числа a и b и возвращающую b-ое по счету число в списке чисел, кратных числу a.

3. Определить функцию, принимающую в качестве аргументов список целых чисел и целое число. Результат функции — список пар (<частное>,<остаток>), составленных по каждому элементу входного списка на основе частного от целочисленного деления каждого элемента списка на входное число и остатка от этого деления.

Вариант 4

1. Определить функцию, принимающую в качестве аргумента список чисел и возвращающую среднее арифметическое его элементов.

2. Определить функцию, принимающую на вход строку и целое число и возвращающую в качестве результата строку, составленную из исходной заменой всех символов, которые больше символа на позиции, указанной входным параметром, этим символом.

3. Определить функцию, принимающую в качестве аргумента две пары, соответствующие комплексным числам в формате (<действительная часть>,<мнимая часть>). Результат функции — частное от деления введенных комплексных чисел.

Вариант 5

1. Определить функцию, принимающую в качестве параметров список символов и число и возвращающую в качестве результата конкатенацию исходного списка и списка, составленного из указанного числа последних элементов и расположенного в обратном порядке.

2. Определить функцию, принимающую на вход список любого типа и значение такого же типа и удаляющую все вхождения указанного значения из списка.

3. Определить функцию, принимающую в качестве аргументов две пары, соответствующие двум точкам на плоскости, и возвращающую расстояние между этими точками.

Вариант 6

1. Определить функцию, принимающую в качестве аргументов список чисел и возвращающую список булевых значений, в котором элементы, соответствующие положительным числам в исходном списке, имеют истинное значение, а соответствующие отрицательным — ложное. Нулевые значения не принимают участие в формировании результирующего списка.

2. Определить функцию, принимающую на вход список положительных целых чисел и возвращающую факториал максимального элемента списка.

3. Определить функцию, принимающую в качестве аргумента список чисел. Результат функции — список пар, в которых первый компонент равен соответствующему значению исходного списка, а второй — его квадрату для четных чисел и третьей степень для нечетных.

Контрольные вопросы

1. Формат записи списков.

2. Какие существуют базовые операции и функции для работы со списками?

3. Формат задания диапазона. Указание шага.

4. Формат записи выражений списков.

5. Формат записи кортежей.

6. Основные отличия кортежей от списков.

7. Какие функции предназначены для извлечения компонентов пар?

8. Каков формат команды определения типа выражения?

9. Формат определения типа функции.

10. Основные типы данных в Haskell.

11. Что такое переменная типа?

12. Что такое класс типов?

13. Основные классы типов в Haskell.

14. Что такое аннотация типа?

Формат 60х84 ¹/₁₆. Бумага тип. № 1. Печать ротапринтная. Уч. изд. л. 2.0. Усл. печ. л. 2.0. Тираж 150 экз. Заказ № 28.

Редакционно-издательский отдел ДГТУ

ИПЦ ДГТУ 367015, Махачкала, пр. Калинина, 70.