 |
Главная |
Формула Ньютона-Лейбница
|
из
5.00
|
Понятие определенного интеграла
Пусть на отрезке  задана функция задана функция  . Разделим этот отрезок точками . Разделим этот отрезок точками  на на  частей, длины которых равны соответственно числам частей, длины которых равны соответственно числам  , где , где  . На каждой из этих частей выберем произвольную точку . На каждой из этих частей выберем произвольную точку
| 
|
 и рассмотрим сумму
и рассмотрим сумму 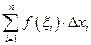 , (1) которая называется интегральной суммой.
, (1) которая называется интегральной суммой.
Определение 1. Определенным интегралом от функции  по промежутку
по промежутку  (обозначается
(обозначается  ) называется предел интегральных сумм (1), если этот предел существует и не зависит от способа разбиения области интегрирования
) называется предел интегральных сумм (1), если этот предел существует и не зависит от способа разбиения области интегрирования  и выбора точек
и выбора точек  .
.
Для каких функций определенный интеграл существует, т. е. соответствующие функции интегрируемы на отрезке  ? Для ответа на этот вопрос надо установить сходимость сумм Дарбу (1). Для этого надо рассмотреть верхнюю и нижнюю суммы Дарбу (значения функции
? Для ответа на этот вопрос надо установить сходимость сумм Дарбу (1). Для этого надо рассмотреть верхнюю и нижнюю суммы Дарбу (значения функции  берутся соответственно самые большие и самые маленькие на каждом промежутке) и доказать, что разность между ними стремится к 0 при
берутся соответственно самые большие и самые маленькие на каждом промежутке) и доказать, что разность между ними стремится к 0 при  . Этот факт интегрируемости функции несложно установить для непрерывной функции на отрезке. Доказаны и более тонкие теоремы об интегрируемости монотонных и кусочно непрерывных функций.
. Этот факт интегрируемости функции несложно установить для непрерывной функции на отрезке. Доказаны и более тонкие теоремы об интегрируемости монотонных и кусочно непрерывных функций.
Свойства определенного интеграла
Теорема 1. (Линейные свойства определенного интеграла) Пусть функции  и
и  интегрируемы на отрезке
интегрируемы на отрезке  (т. е. существуют интегралы
(т. е. существуют интегралы  и
и  ). Тогда справедливы следующие формулы:
). Тогда справедливы следующие формулы:
 (2)
(2)
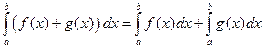 (3)
(3)
 (4)
(4)
 (5)
(5)
Теорема 2. (Свойства аддитивности и монотонности определенного интеграла) Пусть функции  и
и  интегрируемы на отрезке
интегрируемы на отрезке  и
и 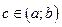 . Тогда справедливы следующие формулы:
. Тогда справедливы следующие формулы:
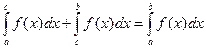 (6)
(6)
 (7)
(7)
Доказательство. Каждый из написанных интегралов является пределом соответствующих интегральных сумм. А для этих конечных сумм написанные формулы, безусловно, справедливы. Теоремы доказаны.
Теорема 3. (Теорема о среднем) Пусть функция  непрерывна на отрезке
непрерывна на отрезке  . Тогда существует значение
. Тогда существует значение 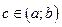 , для которого справедлива следующая формула:
, для которого справедлива следующая формула:
 (8)
(8)
Доказательство. Непрерывная функция на отрезке достигает на этом отрезке свое наименьшее значение 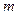 и наибольшее значение
и наибольшее значение 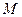 . Тогда
. Тогда  или
или  , откуда
, откуда  и
и  , что равносильно (8).. Теорема доказана.
, что равносильно (8).. Теорема доказана.
Интеграл с переменным верхним пределом
Рассмотрим определенный интеграл  с переменным верхним пределом и непрерывной функцией
с переменным верхним пределом и непрерывной функцией  . Заметим, что
. Заметим, что 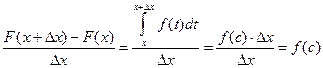 , где
, где  , поэтому, очевидно,
, поэтому, очевидно,  . (9) Итак, справедлива следующая теорема:
. (9) Итак, справедлива следующая теорема:
Теорема 4. (Теорема о производной интеграла с переменным верхним пределом) Производная от интеграла  с переменным верхним пределом равна подынтегральной функции в точке верхнего предела.
с переменным верхним пределом равна подынтегральной функции в точке верхнего предела.
Формула Ньютона-Лейбница
Еще раз рассмотрим определенный интеграл  с переменным верхним пределом и непрерывной функцией
с переменным верхним пределом и непрерывной функцией  . Так как производная от функции
. Так как производная от функции  равна
равна  , то справедлива формула
, то справедлива формула  , где
, где 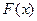 - одна из первообразных функции
- одна из первообразных функции  ,
,  - константа, которую надо найти. Записывая равенство
- константа, которую надо найти. Записывая равенство 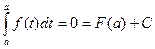 при
при 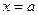 , получим
, получим 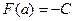 . Следовательно, справедлива формула
. Следовательно, справедлива формула  и нами доказана важная теорема:
и нами доказана важная теорема:
Теорема 5. (Формула Ньютона-Лейбница) Для непрерывной функции  справедлива формула Ньютона-Лейбница для вычисления определенного интеграла
справедлива формула Ньютона-Лейбница для вычисления определенного интеграла 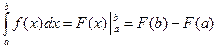 (10)
(10)
|
из
5.00
|
Обсуждение в статье: Формула Ньютона-Лейбница |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

